情境设计抽象概念，问题指引过程探究

张威

[摘  要] “二元一次方程组”具有承上启下的作用，若不能合理设计教学环节，很容易出现思维的断层，也不能充分贯彻该内容所传达的思想. 本文从课例引入、概念抽象、过程设计等方面对“二元一次方程组”的概念教学提出一些建议.

[关键词] 二元一次方程组;情境;课例引入;概念抽象;过程设计

二元一次方程组是解决实际问题的一种重要模型，虽然学生已经掌握了一元一次方程等内容，但从其结构来看相对较为复杂，学生在概念理解上可能存在一定的困难，因此概念教学要采用合理的教学方式，下面是关于其概念教学的一些建议.

遵从认知规律，情境化课例引入

对于“二元一次方程组”的内容，新课标要求学生能够理解概念，并能利用所学知识分析具体问题中的数量关系. 其中概念理解是应用的前提，为完成概念教学，在课例的引入阶段就需要采用情境化的教学方式，而不是通过简单的复述作为课堂开始.

设计情境引入问题时需要注意两点：一是所设计的问题要能够形成良好的探究氛围，问题不宜过难;二是要遵从学生的认知规律，把握知识的衔接点，帮助学生完成旧知到新知的过渡. 因此可以结合中国古代文化，设计如下问题：

《孙子算经》中记载了这样一个有趣的问题，写到“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”用现代话翻译则为：在同一个笼子里有若干只鸡和兔，从笼子的上面数一共有35个头，从笼子的下面数一共有94只脚，问笼子中的鸡和兔子各几只？

而课例引入阶段除了需要注重“引”，还需重视“启”，即利用情境问题来开启学生的智慧，利用已有认知完成问题探索，这个过程就需要教师结合之前的一元一次方程来完成. 在给出该问题后，教师可以首先让学生思考问题是否可以通过列一元一次方程来完成，然后引导学生分别用算术的方法和列二元一次方程的方法尝试解决. 当学生列出二元一次方程后，需要进一步引导学生观察所列方程的“新奇点”，对比一元一次方程来发现二元一次方程组的特征，思考该方程组中的哪个方程可以完全表示情境问题中所有的数量关系，然后对应问题信息完成方程的构建（表1）.

情境化问题的设计是为了通过具体的问题触碰概念的外延，对于学生而言新知的学习是相对困难抽象、难以理解的，因此上述课例设计选取了具有趣味性、代表性、难度适中的古典数学故事. 并利用实际问题激活了数学解题的模型化作用，对于后续培养学生发现问题、思考问题、解决问题十分有利. 而采用引导性的设问方式，触碰了二元一次方程组的概念，可以帮助学生完成后续概念的抽象. 同时，题目信息与方程对照是文字语言与数学语言的进一步沟通交流. 采用这样的教学方式，无形之中引导学生经历了语言转化与模型构建的过程，对于提升学生的读题、释题、化题能力有大有裨益.

符合思维结构，科学抽象概念

新知的学习是一个相对完善的认知体系，除了需要从学生认识的起点开展课堂引导教学，还需要利用科学的探究手段，遵从正确的思维结构来开展. 因此在教学二元一次方程组时就需要按照数、式、运算探究的合理流程——“背景—定义”“表示—求解”.

在引导学生获得鸡兔同笼问题的方程组后，就需要引导学生关注方程组中未知数的次数以及每个方程中未知数的个数，理解x和y就是表示鸡和兔的数量，从而完成二元一次方程组的概念抽象，掌握二元一次方程组的特征，实现“背景”到“定义”的过渡.

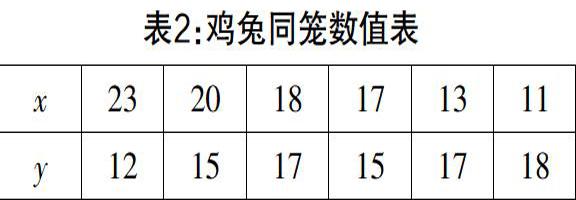
而在由“表示”到“求解”的教学阶段，首先需要使学生理解方程组解的定义，考虑到定义本身相对较为抽象，直接阐述学生难以理解，可以采用科学探究的方式，以多组数的性质呈现. 可以给出如下几组数据，让学生思考其中x和y的值是否符合方程组（如表2），并找出符合方程组的一组值，向学生传达符合方程组的一组值就是二元一次方程组的解的思想.

另外，方程组的解的教学中，也可以采用正反求证的方式，即首先让学生列出两个具体问题的二元一次方程，然后给出几组解，让学生思考哪组解同时满足两个方程，将这组解定义为两个方程的公共解，即二元一次方程组的解.

探究问题：摸球得分.

问题1：如果摸到2个红球和3个绿球的总得分为11分，则每个红球和绿球分别代表多少分？

问题2：再摸一次，摸到3和红球和2个绿球的总得分为14分，则每个红球和绿球分别代表多少分？

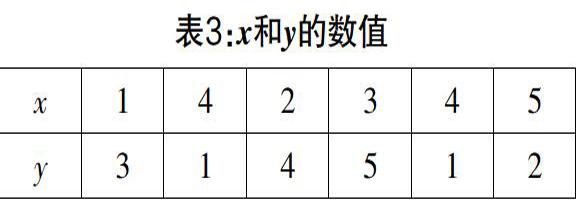
问题3：上述表3的x和y的数值哪些符合问题1，哪些符合问题2，哪些同时符合两个问题？

由“问题”到“问题的解”是一个辨析论证的过程，该过程有两个方面：一是由问题探寻解，二是根据解分析是否符合问题. 正、反论证是一种重要的探究思维，采用这样的教学方式可以让学生体验探析的思维过程，深刻感受解对应方程组的意义，从而充分理解方程组解的概念. 同时，这样的探究过程可以使学生学会用数学的思维方式来思考问题，培养学生的严谨态度和理性思维，而后者才是数学探究活动的真谛所在.

注重过程引导，渗透数学思想

“二元一次方程组”的内容与“一元一次方程”相类似，均是以探究为主，而课堂教学模型的确定应以内容性质为依据，因此应该以知识探究的方式来开展课堂教学. 而探究模型最为核心的内容是“问题”，即利用问题内容的指向性和引导性有序推进教学环节，同时渗透数学的思想方法，用科学的方法引导学生经历知识的探究过程，在掌握探究方法的基础上获得思维的提升.

基于问题指向性设计探究环节时，同样需要遵从知识探究的过程，即“发现问题→做出猜想→论证结论→归纳总结”. 因此在问题设计上可以按照探究模型的基本步骤，设计以问题为指向的环节，使探究环节能够形成连续的问题链. 如探究二元一次方程组的相关概念，可以进行如下设计：给出背景问题→提炼问题猜想→探究论证猜想→归纳抽象概念.

在具体教学中，第一步给出二元一次方程组背景下的情境问题，引导学生利用已有知识尝试解决，学生在列方程的过程中必然会遇到困难，进而会发现问题. 该环节的列方程阶段要渗透模型思想和方程思想，使学生理解数学模型是表达实际问题的重要方式，解方程是解决问题的重要手段. 第二步，对于学生发现的问题要及时引导，如所列方程有几个未知数？获得的解的形式与一元一次方程相比有哪些异同？最终的解是否同时符合两个方程？在该环节的引导过程中要渗透类比思想，让学生通过知识的类比完成“公共解”的问题发现. 第三步则应引导学生对问题现象进行提炼，结合自己的理解归纳猜想. 该阶段教师可以进一步给出几个二元一次方程组和对应的解，加深学生的印象，帮助学生归纳. 在该环节的引导过程中可以渗透对应思想，让学生逐步理解解与方程组的一一对应关系. 第四步，进一步引导学生对提炼的猜想进行论证，参考上述正、反论证的方法，从“两个方程→解”和“解→满足两个方程”两个方面进行解的探析，帮助学生形成“两个方程共同的解就是方程组的解”的观点，为后续的概念抽象打基础. 第五步则应引导学生将总结的观点、结论上升到理论高度，归纳成本节课的概念，该环节需要合理渗透归纳思想，让学生掌握归纳总结的方法，获得思维的提升.

以问题指向为课堂探究的推进方向，以思维节点为探究环节的过渡点，可以在激发学生思考兴趣的前提下，完成思维的自然过渡. 数学的概念和知识发展过程是相對枯燥的，但以问题为指向，符合学生思维过程的探究设计，可以让学生以参与者的身份经历知识转化形成的过程，感受知识衍生的建模过程，从而深刻理解数学的本质.

总之，开展“二元一次方程组”概念课，要精准把握内容的核心概念，化抽象为形象，从具体的内容中衍生概念. 教学设计要考虑学情状况，从实际问题中提炼方程;遵从合理的思维构成，以问题为课堂驱动，开展问题探究教学;渗透数学的思想方法，提升学生的思维层次，使课堂成为激趣启智的园地.