“二元一次方程组”中考试题研究

姜红

像2x-y=5这样，含有两个未知数，并且未知项的次数都为1次，那么这样的整式方程就叫作二元一次方程.二元一次方程有无数组解，若添加条件限定（例如求正整数解），亦可有有限个解，甚至无解.

像2x-y=5，

x+y=4这样，含有两个未知数并且未知项的次数都是1的二元一次方程组成的方程组是二元一次方程组.在七年级下学期，同学们学习了二元一次方程组的解法及其应用.下面以常见的中考题为例，探讨解方程组的基本方法.

一、 二元一次方程组的解法

例1 （2015·重庆）解方程组y=2x-4，①

3x+y=1. ②

例2 （2015·淮安）解方程组：x-2y=3，

3x+y=2.

【解析】这类中考题属于基础题，考查解方程组的基本技能.例1中方程①已经是用含x的代数式表示y的形式，故而适宜使用代入消元法，答案为x=1，

y=-2.例2两种方法均可，但同学们一般还是比较偏向于使用加减消元法，答案为x=1，

y=-1.

【点评】多元方程的解法原则是“消元”.而“消元”的具体方法有代入法和加减法两种.

有时，试题也会涉及“整体代换”等思想方法，比如：

例3 （2015·珠海）阅读材料：善于思考的小军在解方程组2x+5y=3， ①

4x+11y=5.②时，采用了一种“整体代换”的解法：

第（2）题需经整理后，再模仿小军的“整体代换”法，由①得：3（x2+4y2）=47+2xy，即x2+4y2=③，把③代入②得：2×=36-xy，解得：xy=2，则x2+4y2=17.

【点评】此题考查了解二元一次方程组，弄清阅读材料中的“整体代换”方法，是解本题的关键.

二、 二元一次方程组的应用

例4 （2015·北京）《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中，方程术是《九章算术》最高的数学成就.

《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两.问：牛、羊各直金几何？”

译文如下：“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两.问：每头牛、每只羊各值金多少两？”

设每头牛值金x两，每只羊值金y两，可列方程组为__________.

【解析】根据“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两”，得到等量关系，即可列出方程组. 5x+2y=10，2x+5y=8.

【点评】这类问题中两个量呈一次关系，往往可以抽象出二元一次方程组，解决本题的关键是找到题目中所存在的等量关系.

例5 （2015·佛山）某景点的门票价格如表：

某校七年级（1）、（2）两班计划去游览该景点，其中（1）班人数少于50人，（2）班人数多于50人且少于100人，如果两班都以班为单位单独购票，则一共支付1 118元，如果两班联合起来作为一个团体购票，则只需花费816元.

（1） 两个班各有多少名学生？

（2） 团体购票与单独购票相比较，两个班各节约了多少钱？

【解析】（1） 设七年级（1）班有x人、七年级（2）班有y人，根据如果两班都以班为单位单独购票，则一共支付1 118元，如果两班联合起来作为一个团体购票，则只需花费816元建立方程组12x+10y=1 118，

【点评】本题考查了列二元一次方程组解实际问题的运用、二元一次方程组的解法的运用，解答时建立方程组求出各班的人数是关键.

三、 与二元一次方程组有关的综合题

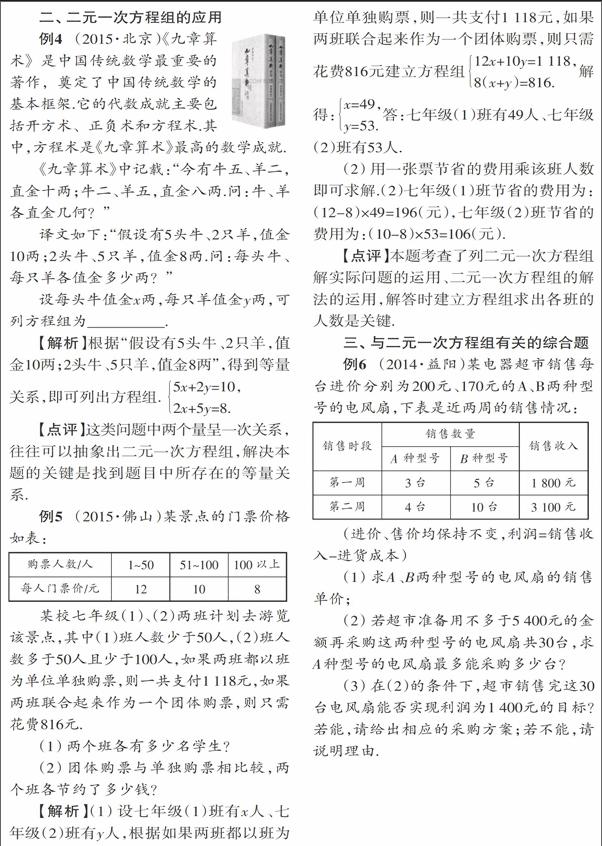
例6 （2014·益阳）某电器超市销售每台进价分别为200元、170元的A、B两种型号的电风扇，下表是近两周的销售情况：

（进价、售价均保持不变，利润=销售收入-进货成本）

（1） 求A、B两种型号的电风扇的销售单价；

（2） 若超市准备用不多于5 400元的金额再采购这两种型号的电风扇共30台，求A种型号的电风扇最多能采购多少台？

（3） 在（2）的条件下，超市销售完这30台电风扇能否实现利润为1 400元的目标？若能，请给出相应的采购方案；若不能，请说明理由.

（2） 设采购A种型号电风扇a台，则采购B种型号电风扇（30-a）台，根据金额不多于5 400元，列不等式得：200a+170（30-a）≤5 400，解得：a≤10.所以超市最多采购A种型号电风扇10台时，采购金额不多于5 400元.

（3） 设利润为1 400元，列方程（250-200）·a+（210-170）（30-a）=1 400，解得：a=20.

若不符合（2）的条件，可知不能实现目标.∵a≤10，∴在（2）的条件下超市不能实现利润1 400元的目标.

【点评】本题考查了二元一次方程组和一元一次不等式的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系和不等关系，列方程组和不等式求解.这类试题把二元一次方程组与一次不等式结合起来考查，难度有所加大.

（作者单位：江苏省南京师范大学附属中学江宁分校）