基于课例研究寻找数学课堂灵魂

李织兰 韦仕强

【摘要】本文以证明数学命题“圆内所有的线段，直径最长”的教学片段为例，论述在数学教学中培养学生的理性思维的途径，提出数学教学应突显思维过程，让学生感悟数学思想，从而培养学生的理性精神。

【关键词】数学课堂灵魂 思维过程 数学思想 理性精神

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2018）11A-0038-04

日本数学家、教育家米山国藏说过：“学生们在初高中所学到的数学知识，几乎没有什么机会应用，很快就会忘掉，然而不管他们从事什么业务工作，唯有深深地铭刻于脑际的数学精神和数学思想方法，长期地在他们的生活和工作中发挥着重要作用。”数学文化的价值主要在于数学对人们的观念、精神以及思维方式的养成所具有的重要的影响。数学对人类文明最大的贡献是理性精神。理性精神是一种推演的精神、逻辑的精神，是一种求真的精神。发挥数学的文化教育功能，就应积极地培育理性精神、演绎理性的力量。数学课堂的灵魂是什么？我们通过研究证明“圆内所有的线段，直径最长”这一数学命题的教学片段得到了答案：突显思维过程，感悟数学思想，培养理性精神。

片段一：彰显自主，让学生有真探索

（教师采用“自主尝试—小组交流—全班反馈”的教学策略，让学生在小组内讨论、向全班交流自己探究得到的“圆的性质”）

生1：我们小组得出了“圆内所有的线段，直径最长”的结论。

师：你们是怎么知道的？

生1：我们量出圆内5条线段的长度，直径AB=7.8cm，半径OA=3.9cm，线段CD=4.6cm，线段EF=2.3cm，线段CG=6.3cm。所以，我们发现了“圆内所有的线段，直径最长”。

师：你们真聪明，你们发现了老师没告诉过你们并且书上没写的性质！大家齐声拍手表扬她。

【评析】

教师应着眼于落实“四基”、培养“四能”、关注学生全面发展的核心素养设计教学活动。合情推理用于探索思路、发现结论，从三年级开始，每册教材有计划地编排一个“探索规律”的专题活动，有利于学生形成“实验—归纳—猜想”的思维习惯，从而培养学生的合情推理能力。安排这一教学环节，注重探索规律的经验积累和数学思想方法的感悟，凸显了探索规律的教学价值。

片段二：巧妙设疑，让学生有真思考

师：刚才那位同学发现的这个结论（圆内所有的线段，直径最长），还需要验证吗？

生1：道理明摆着，没有必要了。（多数学生认同）

师：前些天的一个早上，老师带着一台测量身高的设备在学校门口测量了57名进校学生的身高，所测量的学生的身高都没达到170cm，所以我们得出了一个结论，“我们学校的学生身高都不超过170cm”。刚说完就来了一名6（2）班的同学，他的身高是173cm，老师“被打脸”。为什么老师会“被打脸”呢？

生2：你还没量完我们学校所有的学生的身高，你就下结论了。

师：我明白了，我们只能对我们测量过的对象下结论。那刚才你们量完了圆内所有的线段了吗？你们能保证圆内每一条线段的长度都不超过圆的直径吗？

生1：不能！

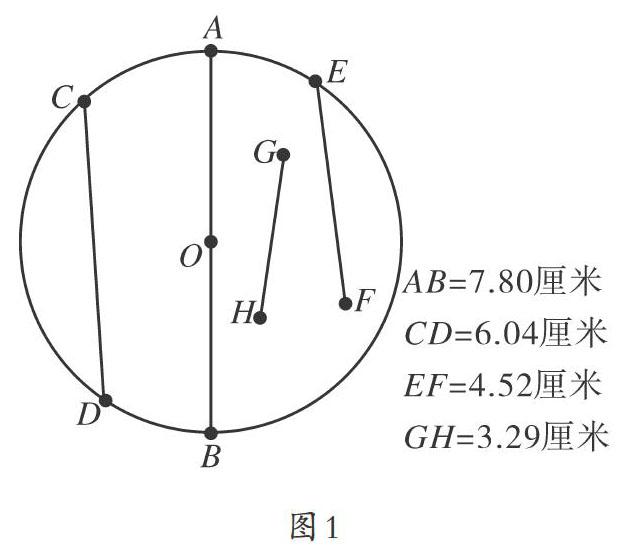
师：下面我通过多媒体课件来验证一下。（在几何画板上分别拖动点C，D，E在圆上运动，拖动点F，G，H在圆内变动，指导学生观察线段CD，EF，GH的长度，如图1）我们通过实验验证了“圆内所有的线段，直径最长”，这样可以了吗？

生（齐声回答）：可以！

生3：也不可以，变换线段和点，只是测量更多圆内的线段长度，但圆内有无穷多条线段，圆内有无穷多点，所以，这些线段的长度不可能量完的。

师：同学们比我想得更周全，刚才演示的几何画板课件只是让我们更加相信“圆内所有的线段，直径最长”这个结论是正确的，但确实不可以用实验的方法对无穷多的对象下结论，因为我们“量不完”。看来要确定“圆内所有的线段的长度都不超过圆的直径”必须用数学“理性”的方法了。

【评析】

在学生提出猜想后，教师利用多媒体课件验证了这一猜想，不仅激发了学生验证猜想的兴趣，而且让学生认识到通过实验验证猜想的局限性，逐步渗透给学生知道：合情推理的结论可能是正确的，也可能是错误的，还需要依靠演绎推理去证明。

数学的严谨性和抽象性决定了它是以理性见长的学科，数学教学的目的在于发展学生的数学思维，思考是思维的重要表现。学生遇到了疑问，也就是遇到了數学问题，就会去思考。教师应根据教学内容巧妙设疑，让学生自觉地思考、乐意去思考。

片段三：分类讨论，领悟数学思想方法

师：圆内线段有无穷多，既然不能一条一条地去量，我们能不能把它们分成若干类，一类一类比较后再下结论呢？

生1：这种分类讨论的方法肯定比一条一条地去讨论要好些。

师：那我们就做一做！

（回顾已学的知识：什么是直径？什么是半径？它们有什么关系？直径是两个端点在圆周，并且过圆心的线段;半径是圆周上的点与圆心的连线;一条直径的长度等于两条半径的长度）

师：我们讨论的线段要与直径比长短，线段是由两个端点确定的，直径的两个端点在圆周。想一想，将圆内所有的线段依据什么标准来分类更适合我们进行讨论？

生2：依据线段的两个端点是否在圆周上来分。

师：这样我们可以“不重不漏”地把圆内的线段分成……

生2：分为三类。两个端点都在圆周、一个端点在圆周（另一个端点不在圆周）、两个端点都不在圆周。

【评析】

分类讨论是一种重要的数学思想方法。运用分类讨论，往往能使繁杂的问题清晰化、简单化。本例中，在无法穷尽的情况下，选择各种类型的样本（典型代表）进行研究，用样本（典型代表）反映整体。分类的过程，可以培养学生思考的周密性、条理性，而分类讨论，又可以促进学生研究问题、探索规律的能力的发展。

教师在教学中渗透分类思想时要研究的问题主要有：怎样驱动学生有目的地分类？怎样引导学生找到合适的分类标准？分类如何做到不重不漏？怎样才能形成分类讨论的意识？

片段四：逻辑推理，孕育理性精神

师：“先易后难，化难为易”是我们解决数学问题的一大“诀窍”。我们应先选哪一类线段与直径比长短呢？

生1：第一类（两个端点都在圆周的线段），因为直径也在这一类。

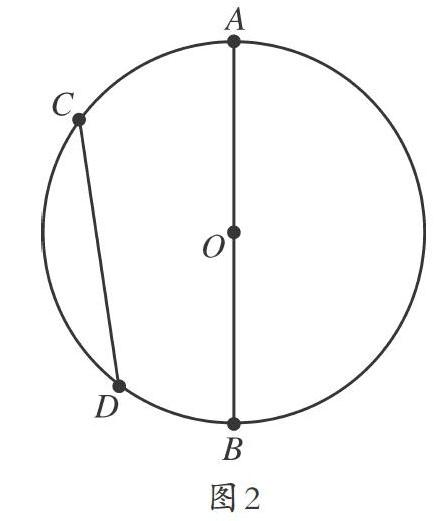
师：好，我们用什么辦法来比较线段CD与直径AB的长短？

生2：量一量。

师：量是“感性”的方法，只能对量过的特殊圆和线段下结论，对任何一个圆内的、所有的、无穷多的线段是不能确定的，所以，我们不能用“量”，还得思考更“理性”的方法。注意观察，直径是由OA，OB两条半径构成的，要比较AB与CD的长短，是否应该作两条与线段CD有关的半径呢？找这两条半径与CD的关系？

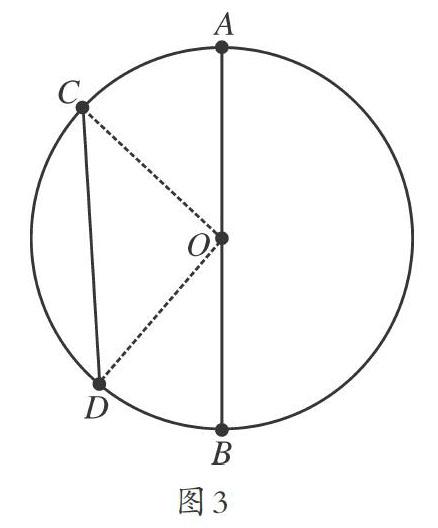
生3：应该可以，连接圆周上的点与圆心的线段就是半径，所以，CO和DO就是两条半径。

生4：我知道结论了，CD<AB。因为，在三角形CDO中，两边之和大于第三边，因此CO+DO>CD，也就是说CD的长度小于两条半径的长度之和，所以CD的长度小于直径AB的长度。

师：现在我们可以说“所有两个端点都在圆周上的线段的长度都不超过直径的长度”吗？

（部分学生说“能”，部分学生说“不能”）

师：到是“能”还是“不能”，就看我们画的线段的“代表性”，CD能不能代表所有的“两个端点都在圆周上的线段”。

生5：CD的两个端点在直径的同一侧的半圆上，算是特殊的吧，还不是任意的“两个端点都在圆周上的线段”。

生3：CD可以代表“两个端点在直径同一侧半圆上的线段”。

师：现在谁能严谨地表达我们刚才推理得出的结论。

生5：任意一条两个端点在直径同一侧半圆上的线段的长度不超过直径。（板书）

生1：我发现“两个端点不同在直径一侧半圆上的线段”，也能得出一样的结论。

（教师展示图4）

师：其他同学看明白了吗？

生：明白了。

师：所有的“两个端点都在圆周的线段”又可以不重不漏地分为两类——两个端点同在直径某一侧的半圆上的线段、两个端点不同在直径某一侧半圆上的线段。根据我们上述的分类讨论和推理，现在我们可以完全肯定地说“所有的两个端点都在圆周上的线段的长度都不超过直径的长度”。

师：现在我们的任务是“化未知为已知”。想一想，我们可以怎样将“一个端点在圆周的线段”“两个端点都不在圆周的线段”这两种线段转化为“两个端点都在圆周的线段”。

（学生小组讨论、自主探究、代表汇报，将第二类、第三类圆内的线段CD延长成第一类线段，展示成果如下）

CD<CE<AB

CD<EF<AB

师：同学们，经过以上逻辑推理，我们得到圆内所有三种类型的线段的长度都不超过直径的长度。因此，我们得到了“圆内所有的线段，直径最长”的结论。

【评析】

数学对人类文明最大的贡献是什么？是理性精神。理性精神是一种推演的精神、逻辑的精神，是一种求真的精神。发挥数学的文化教育功能，就应积极地培育理性精神、演绎理性的力量。在小学数学教学中启蒙学生的理性精神是非常重要的，不仅能够提高学生学习数学的积极性，还能够让学生学会理性思考，形成理性思维，感悟理性的力量，提升学生综合能力和核心素养。

片段五：小结

师：通过对这一个问题的探究，你有哪些收获？

生1：实验可以发现规律，但还必须验证。（实验用于探索思路、发现结论;要通过演绎推理去证明结论。学习到实事求是、言必有据的科学态度）

生2：学会了用推理方法验证规律。（逻辑推理和计算证明的方法）

生3：学会了分类讨论的推理方法。（找到合适的分类标准，做到不重不漏，选择各类代表来反映整体，即得到这类对象都具有的性质）

生4：“先易后难，化难为易”是学习数学“诀窍”。

【板书、板图设计】

本课教学是高校教师与小学一线名师合作，准确解读课程标准，针对课改热点、难点，精心设计出来的，让学生在学习中感悟分类思想和化归思想，体验逻辑推理的方法，启蒙理性思维，孕育理性精神。

（责编 刘小瑗）