恒化器中单营养食物链的微生物培养模型的定性分析

王永丽

(江苏财会职业学院基础部，江苏连云港 222061)

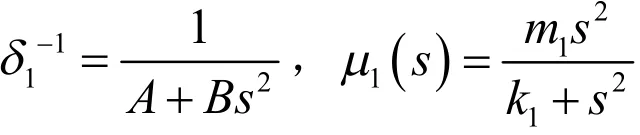
1 具有Holling Ⅲ类功能反映函数的单食物链模型

模型如下：

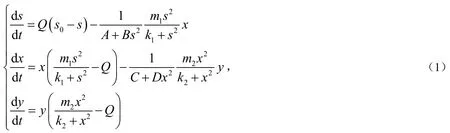
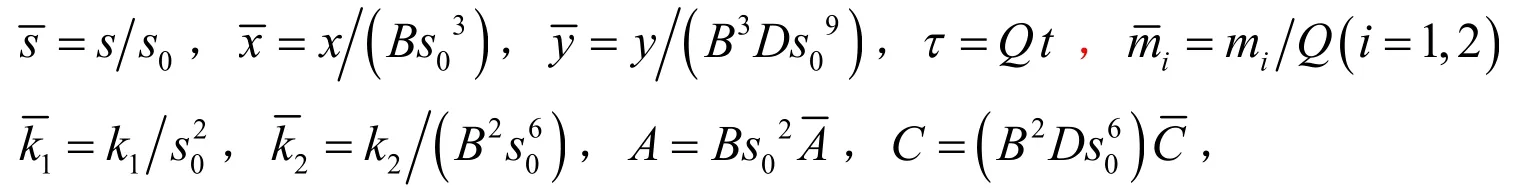
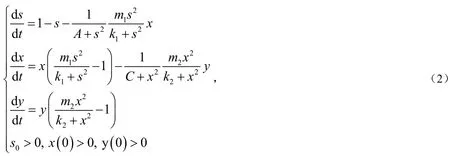
2 模型的定性分析

考虑系统(2)的平衡解，为此解方程组

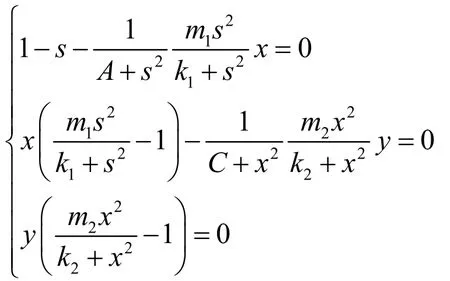
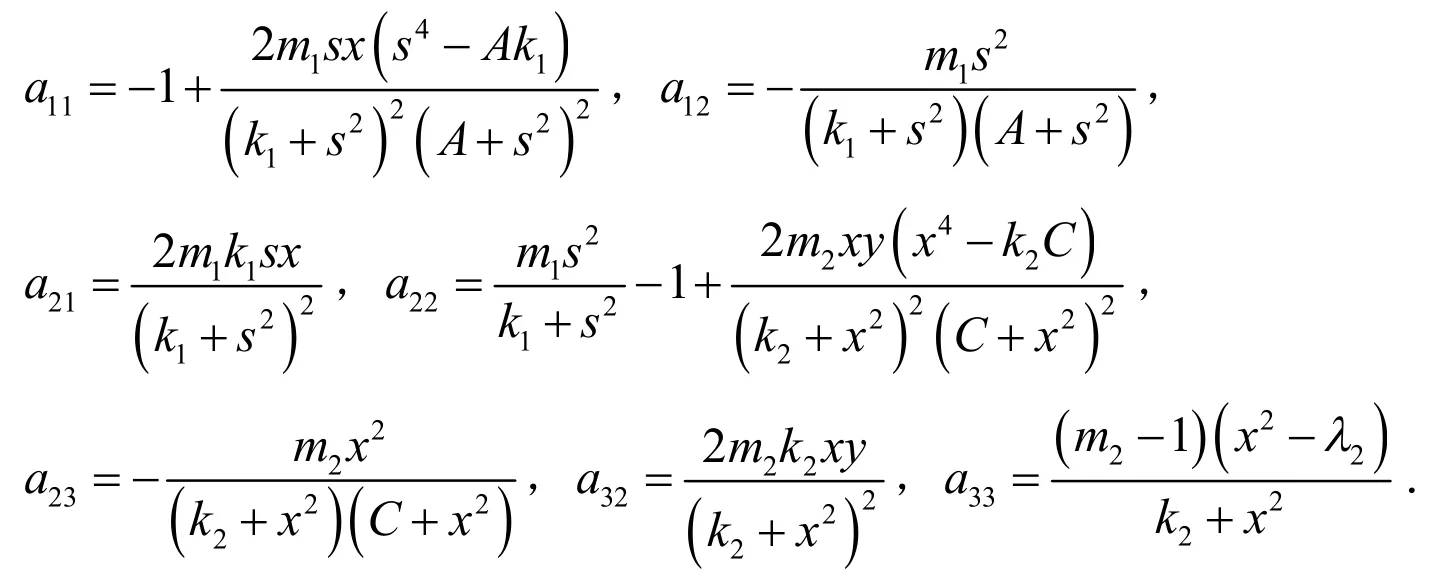
2.1 模型平衡点的稳定性分析

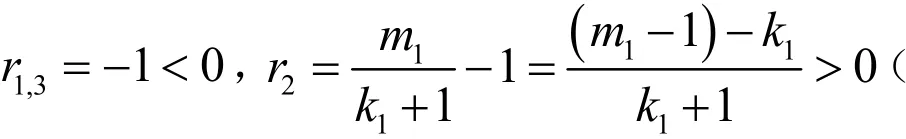
系统(2)在E1处的特征方程为：

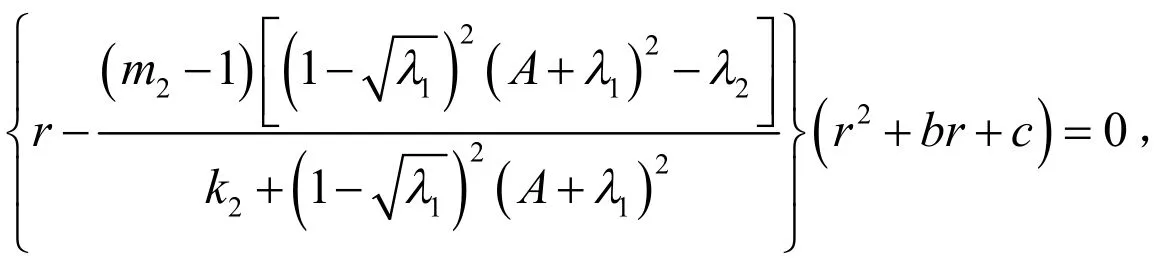
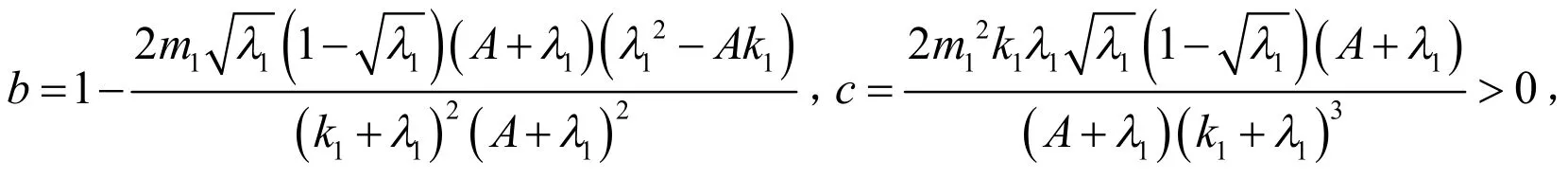
系统(2)在E2处的特征方程为，其中

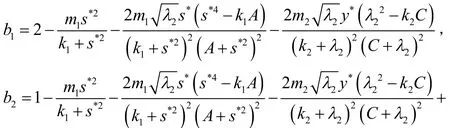
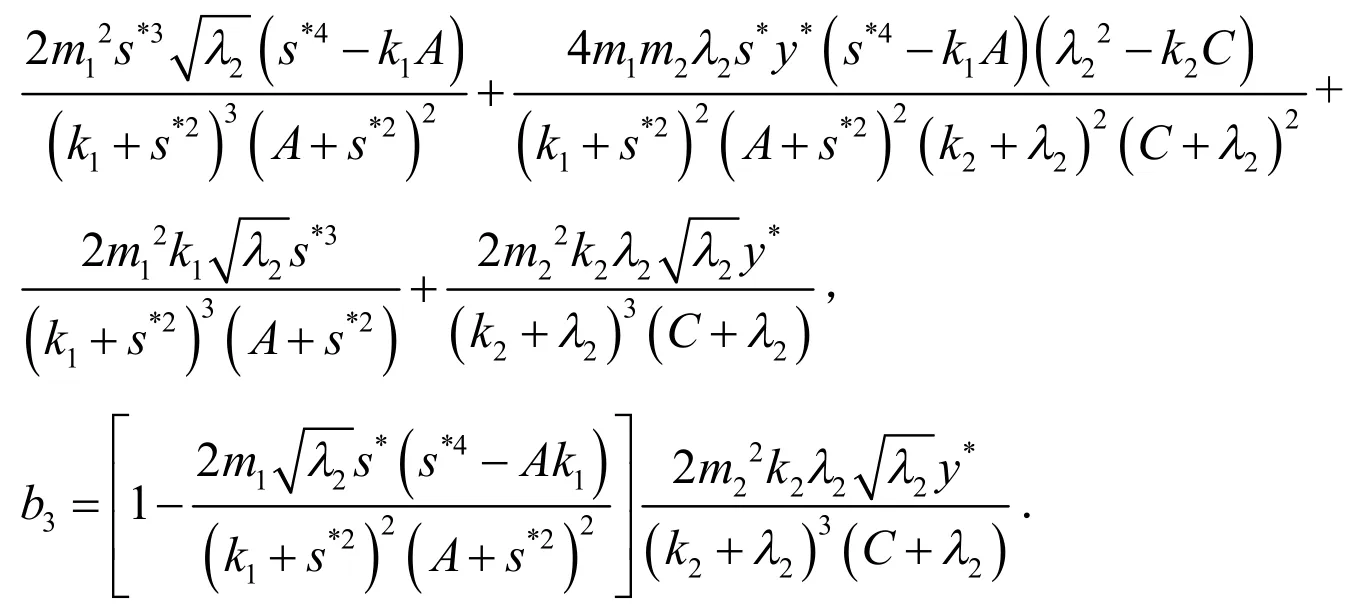
时，由Hurwitz判别法知，平衡点E2是稳定的.

2.2 模型存在正向不变集

定理3 系统(2)存在正向不变集：

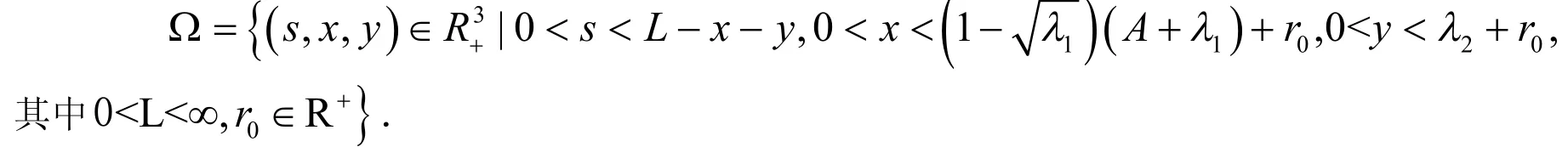
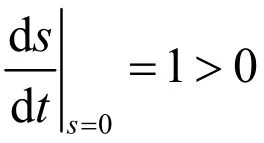
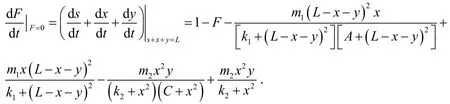
因为x,y有界，均为正常数，所以对充分大的L，有，即任意从出发的轨线，在t→+∞时，轨线穿过平面F=0进入区域Ω，故Ω为系统(2)的不变集.

3 结 语

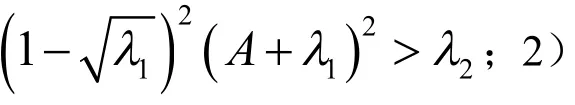
[1] 陈兰荪，陈键.非线性生物动力系统[M].北京：科学出版社，1993：45-100.

[2] 王凯，滕志东.一类具有营养液循环的脉冲注入恒化器模型的动力学研究[J].生物数学学报，2014，29(2)：216.

[3] 王永丽.Chemostat中单营养食物链模型的全局稳定性分析[J].宝鸡文理学院学报(自然科学版)，2015，35(4)：14.

[4] 李姣，孟琳琳，原三领.具有多个参数扰动的随机恒化器模型研究[J].上海理工大学学报(自然科学版)，2013，35(6)：529.

[5] Li H Y, Zhang R. Stability and optimal harvesting of a delayed ratio-dependent predator-prey system with stage structure [J]. J Biomath, 2008, 23(1):49.

[6] 王永丽.具有非常数消耗率的单营养食物链2种群微生物模型定性分析[J].成都大学学报(自然科学版)，2016，35(1)：47.

[7] 阎恩让，王爱丽.具有三个成长阶段的多种群捕食模型的全局稳定性[J].福州大学学报(自然科学版)，2014，42(4)：515.

[8] 王晖，李冬梅，郭秀微.一类具有时滞的Lotka-Volterra捕食系统的持久性与全局稳定性[J].哈尔滨理工大学学报，2009，14(6)：75.