分数阶Qi混沌系统的动力学分析及DSP实现
雷腾飞,王艳玲,苏 敏,陈晓霞
(1.齐鲁理工学院电气信息工程学院,山东济南 250200;2.河北工业大学理学院,天津 300401)
分数阶微分方程在许多应用科学领域能准确地描述自然现象,如材料记忆、电力分形网络、机器人与机械阻尼特性等[1].近年来,随着混沌动力学理论研究的深入与完善[2],从而使得分数阶混沌系统的探讨与研究已成为新的研究领域[2].在分数阶混沌系统研究领域中,主要以经典的混沌系统为研究对象,重新引入分数阶微积分算子,即提出了许多分数阶混沌系统[3-16],文献[3-9]所提出的混沌系统均是可称为类分数阶Lorenz混沌系统,有一类Qi系统因含有三个非线性项,故系统混沌更为复杂[17].迄今为止,许多科学工作者在分数阶混沌系统同步控制方面成果颇丰,但阐述分数阶混沌系统动力学分析相关文献较少[10-16].研究分数阶系统的前提为分数阶的定义,由于分数阶微积分的定义众多[10],使得许多研究结果存在一定区别[11].其中,对于分数阶Qi超混沌系统动力学分析,贾红艳等[13]利用频率法进行了分岔图与李指数的绘制与分析.Qi混沌系统因具有三个非线性项[17],使得与经典的Lonrez系统、Chen系统与LV系统具有不等价的拓扑,故对分数阶Qi混沌系统的动力特性的探究讨论尤为重要,而现有文献运用分岔图、Lapunov指数分析分数阶混沌系统的研究大部分采用复频率分析法[12-14],所以利用Adomain分析分数阶Qi混沌系统的动力学(复杂度)对于认识分数阶混沌系统的形成机理具有重要意义.
本文针对一类临界分数阶混沌系统即分数阶Qi混沌系统,首先,对分数阶Qi混沌系统的非线性项进行了Adomian分解法,得出了系统的混沌吸引子.其次,为了说明系统状态随参数变化的特点,同时研究了0.95阶的Qi混沌系统的分岔图与复杂度图以及分岔空间.最后,利用DSP实现其分数阶混沌系统.进一步说明了系统的客观存在性,为更好应用于图像、文字视频加密领域提供了参考价值[18].
1 分数阶Qi混沌系统
根据经典Qi混沌系统则可引入分数阶算子,得到分数阶Qi混沌系统为:

对系统(1)进行非线性项的分解,截取前6项
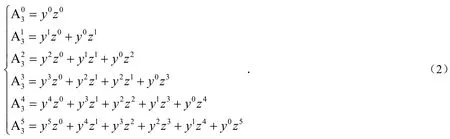
给定初始状态

根据Adomian分解法和分数阶微积分性质得

将相对应的变量赋系数值,令

根据Adomian分解法和分数阶微积分性质得

从而,得出系统的方程解

其中x,y,z为系统变量,a,b,c为系统参数,当,运用Matlab软件对其进行Adomain分解下的Qi系统数值仿真,即可得出系统(1)的混沌轨迹图如图1所示.

图1 系统轨迹图Fig 1 Trajectory Diagram of System
2 分数阶Qi混沌系统分岔图与复杂度
为进一步分析系统参数对分数阶Qi混沌系统的影响,就a,b,c三个主要参数对分数阶临界混沌系统的分岔图与复杂度的影响进行研究.
2.1 参数a的变化
改变分数阶Qi混沌系统对应的参数a,,系统的分岔图与复杂度如图2所示.由图2可知系统是以倍周期(PDB)分岔的行为脱离混沌行为,即随着
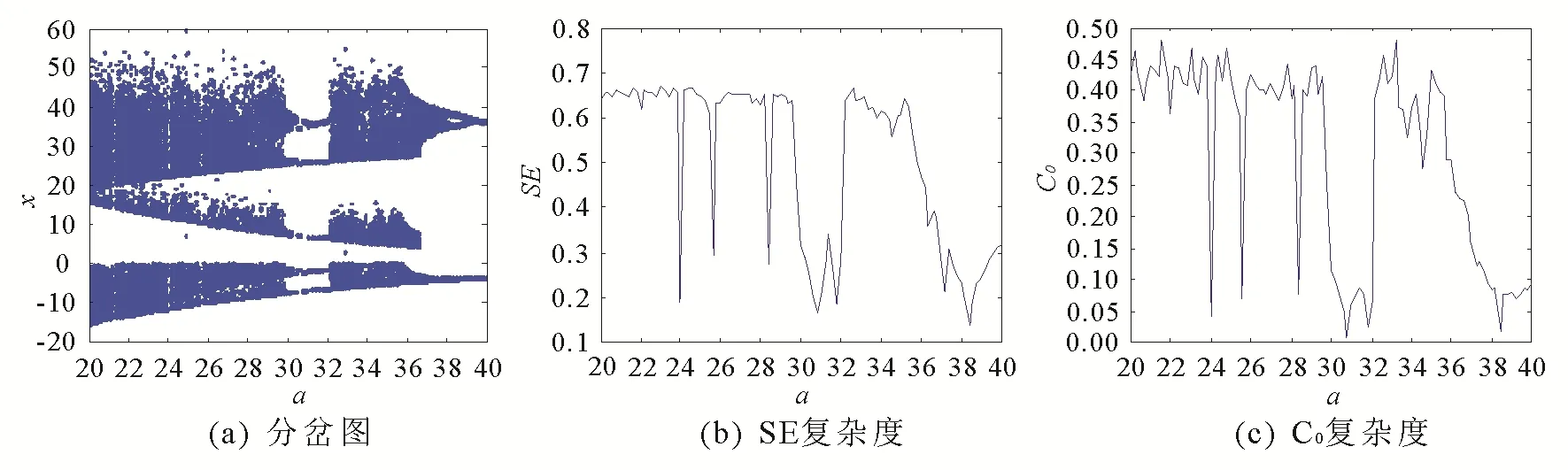
图2 a变化时系统(1)的分岔图复杂度Fig 2 The Bifurcation Diagram and Complexity of System (1) in a Change
参数a逐步减小,呈现倍周期进入混沌态.或[31.2,37]属于混沌状态,从分岔图中可以看出此区间有许多混乱的点,系统此时的SE复杂度与C0复杂度相对较大或(37,40)属于周期状态;从分岔图中可以看出此区间点比较稀疏且成线出现,系统此时的SE复杂度处于0.3左右,C0复杂度属于0.05左右,系统复杂度相对较低;系统分岔图与系统复杂度基本一致.为进步验证以上结论,给出了参数a某些具体值下系统的相图如图3所,其中(a)图为周期二,(b)图为周期四,(c)图为周期二,(d)图为周期一.

图3 a变化时系统(1)的相图Fig 3 Phase Diagram of System (1) in a Change
2.2 参数b的变化

图4 b变化时系统(1)的分岔图与复杂度Fig 4 The Bifurcation Diagram and Complexity of System (1) in b Change
2.3 参数c的变化
改变参数c,,系统的分岔图与复杂度如图5所示.由图5可知系统是拟周期的过程进入混沌态的.或[24.5,27]属于周期状态,系统此时的SE复杂度与C0复杂度较小;剩余的区域系统属于混沌状态,此时系统的SE复杂度较大.可以看出系统分岔图与系统复杂度基本一致.
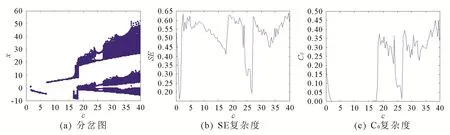
图5 c变化时系统(1)的分岔图与复杂度Fig 5 The Bifurcation Diagram and Complexity of System (1) in c Change
3 混沌系统的数字实现
现今混沌系统最常见的实现方法为模拟电路实现,随着数字电子电路和微型处理器快速发展,运用微型处理器(MCU、DSP、FPGA)实现其混沌系统已成为混沌系统实现及应用的热点.为了更好实现分数阶Qi混沌系统,本文采用TI公司的数字信号处理芯片(DSP)TMS320F28335,DSP以强大的信号处理能力备受工程师的关注.数字信号必须转化为模拟信号才可在示波器上实时显示,数字转化为模拟(DAC)转化器采用芯片DAC8552.为方便处理,DSP与PC机的通讯方式采用普通串口RS232,串口转换芯片采用MAX3232.因TMS320F28335为浮点型且精度高、运算快,主频为150MHz,可解决因算法复杂而使得处理器运行缓慢的问题,即可满足分数阶Qi混沌系统各方面要求.在DSP实现分数阶Qi混沌系统存在一个关键性的问题——数据处理.离散数据通过基本Adomian分解法产生,然后将离散值通过DMA送给D/A转化,在D/A转换数字量必须为整,所以某些数字需要放大后再送达D/A转换器.一般为了PC机处理方便,则将混沌序列中的每一位换成ASCII码即可,具体DSP硬件框架图如图6所示.
数字电路对分数阶混沌系统实现拟合采用Adomian分解法,参看(2)式-(9)式,一般将DSP产生的混沌序列值取小数点后四位,对初值后的一段序列采用丢弃法,即取3000-15000之间的序列,示波器观察吸引子如图7.

图6 DSP硬件框架图Fig6 DSP Hardware Frame Diagram
6 结 论
本文基于Adomian分解法,研究了一类经典的分数阶Qi混沌系统.从系统吸引子、分岔图、复杂度等数值仿真分析0.95阶次Qi混沌系统基本动力学行为.为了验证系统存在性并应用到工程项目中,运用数字芯片DSP实现其分数阶Qi混沌系统,从示波器观察出结果与Matlab仿真结果一致,从而进一步说明了分数阶Qi混沌系统的存在性与可实现性,为分数阶Qi混沌系统的控制及其在混沌通信保密等方面的应用奠定了基础.
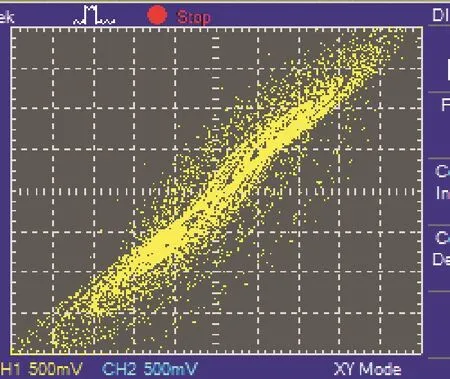
图7 示波器观察的系统吸引子Fig 7 The System Attractor of Oscilloscope Observation
[1] Hilfer R. Applications of fractional calculus in physics [M]. New Jersey:World Scientific, 2001:86-90.
[2] Mandelbrt B B. The fractal geometry of nature [M]. New York:Freeman, 1983:22-34.
[3] Lu J G. Nonlinear observer design to synchronize fractional-order chaotic system via a scalar transmitted signal [J].Physica A, 2006, 359:107-118.
[4] 王震,孙卫.分数阶Chen混沌系统同步及Multisim电路仿真[J].计算机工程与科学,2012,34(1):187-192.
[5] Wu X J. Chaos in the fractional order unified system andits synchronization [J]. Chinese Phys, 2007, 16(7):392-401.
[6] 雷腾飞,陈恒,尹劲松,等.分数阶LV混沌系统的分析与电路模拟[J].曲阜师范大学学报(自然科学版),2015,41(2):35-41.
[7] Bao B C, Liu Z, Xu J P. New chaotic system and its hyperchaos generation [J]. J Systems Eng Elect, 2009, 20(6):1179-1187.
[8] 刘崇新.一个超混沌系统及其分数阶电路仿真实验[J].物理学报,2007,56(12):6865-6873.
[9] Yuan L G, Yang Q G. Parameter identification and synchronization of fractional-order chaotic systems [J]. Commun Nonlinear Sci, 2012, 17:305-316.
[10] Podlubny I. Fractional differential equations [J]. New York:Academic Press, 1999:21-25.
[11] Li C P, Deng W H. Remarks on fractions derivatives [J]. Appl Math Comput, 2007, 187:777-784.
[12] 贾红艳,陈增强,薛薇.分数阶Lorenz系统的分析及电路实现[J].物理学报,2013,62(14):140503.
[13] 薛薇,肖慧,徐进康,等.一个分数阶超混沌系统及其在图像加密中的应用[J].天津科技大学学报(自然科学版),2015,30(5):67-71.
[14] 陈恒,雷腾飞,王震,等.分数阶 Lorenz超混沌系统的动力学分析与电路设计[J].河南师范大学学报(自然科学版),2016,44(1):59-63.
[15] 杨志宏,屈双惠,马志春,等.一类分数阶四翼混沌系统的动力学特性及其多元电路实现[J].华中师范大学学报(自然科学版),2016,50(5):665-671.
[16] 雷腾飞,胡庆玲,尹劲松.基Adomian分解法的分数阶Chen混沌系统的动力学分析与DSP实现[J].曲阜师范大学学报(自然科学版),2016,42(3):76-82.
[17] Qi G Y, Chen G Y, Wyk M A, et al. A four-wing chaotic attractor generated form a new 3-D quadratic autonomous system [J]. Chaos Soliton Fract, 2008, 28(3):705-721.
[18] Wang Z, Lei T F, Xi X J, et al. Fractional control and generalized synchronization for a nonlinear electromechanical chaotic system and its circuit simulation with Multisim [J]. Turk J Electr Eng Co, 2016, 24(3):1502-1515.

