Bloch型空间上的加权微分复合算子
侯晓阳,许 毅,陈 伟
(1.温州商学院基础部,浙江温州 325035;2.温州大学数理与电子信息工程学院,浙江温州 325035)
1 有关定理及推论
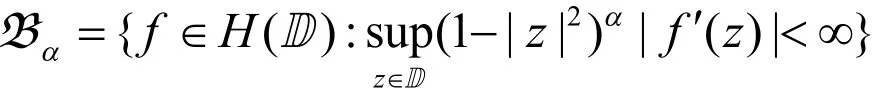
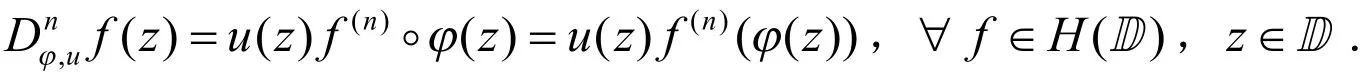
若n=0,则就是加权复合算子,如果再有u(z)≡1,则为复合算子Cφ.
Madigan K和Matheson A在文[2]中研究了Bloch空间和小Bloch空间上复合算子Cφ的有界性和紧性问题;LouZ[3]研究了不同权Bloch型空间之间的复合算子Cφ,对于H∞空间上的加权复合算子uCφ的有关结论,可见文[4-8]及相应文献;Stevic[9-10]和刘永民等[11]等研究了混合范数空间和Bloch空间,以及Hardy空间上的加权微分复合算子的有界性和紧性问题.文献[12]研究了单位圆盘上从BMOA空间到Bloch型空间的加权微分复合算子的有界性和紧性,得到:
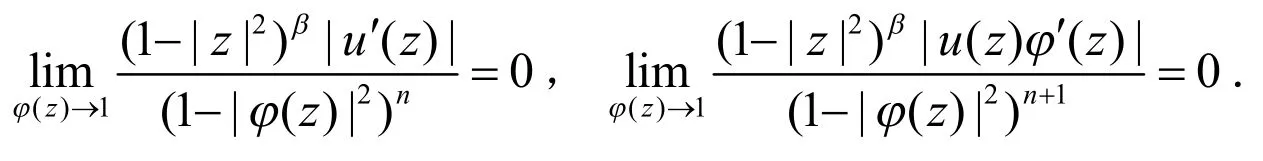


当α=1时,即为上述定理A,定理B;当n=1,时,则算子,可得文[13]主要结论:
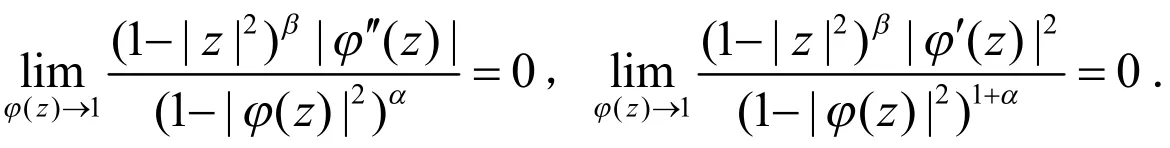
定理的证明主要采用待定系数法确定检验函数,本文出现的字母C表示与变量z,w等无关的常数,为方便起见,不同的地方可以表示不同的常数.
2 引 理
引理1 对任意正整数n,f∈Bα,存在常数C(只与权值α有关),使得

引理1可见文[14]定理5的证明过程,下面的紧性判断引理见文[15]定理3.11,取X=Bα,Y=Bβ,类似证明可得.
3 定理的证明
定理1的证明:充分性.若条件(1)(2)成立,结合引理1,可得:
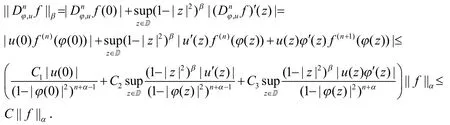

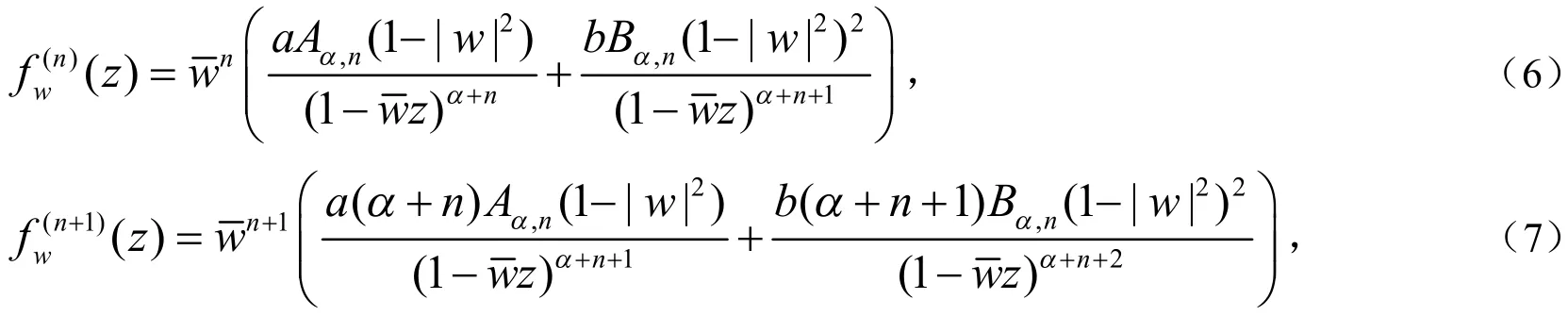


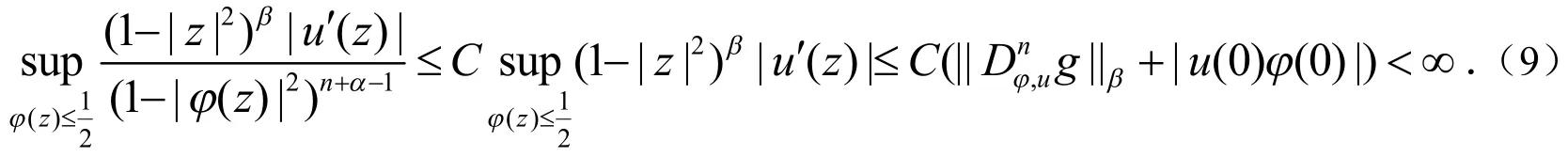
综合(8)和(9)可知(1)式成立.
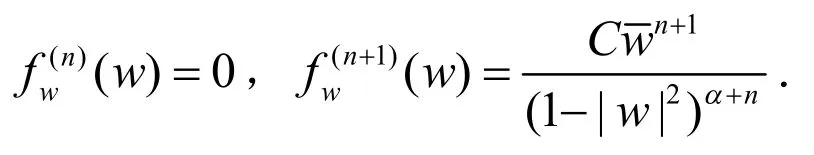
定理2的证明:充分性.对Bα中的任意有界序列,有fk在D的紧子集上一致收敛于0,由引理2,只需证明.以下不妨设
由条件(3)和(4),∀ε>0,当时,有:


结合(10)和(11)式,以及引理1,可得:

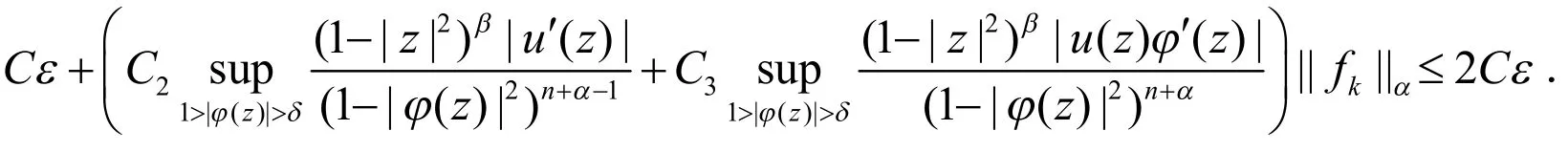


当|z|≤r<1时,有:
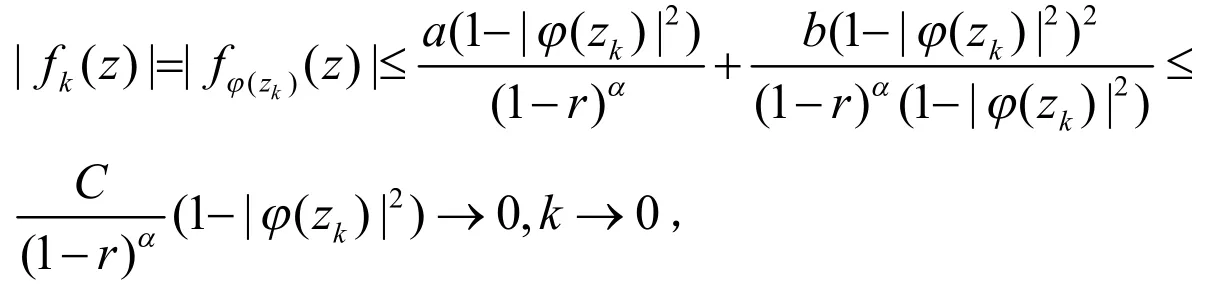
即fk(z)在D的紧子集上一致收敛于0.故由引理2,结合式(14)式得到:
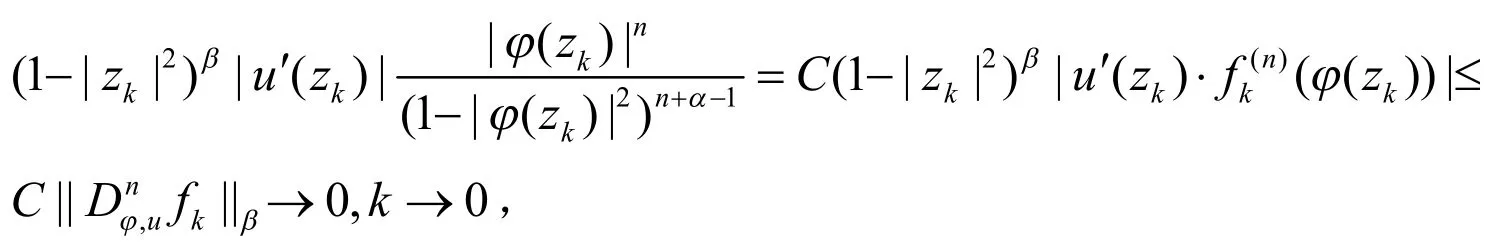
[1] Zhu X L. Products of differentiation, composition and multiplication from Bergman type spaces to Bers type spaces[J]. Integr Transf Spec F, 2007, 18(3/4):223-231.
[2] Madigan K, Matheson A. Compact composition operators on the Bloch space [J]. Trans Amer Math Soc, 1995, 347:2679-2687.
[3] Lou Z. Composition operators on Bloch type spaces [J]. Analysis, 2003, 1(1):81-95.
[4] Shi J H, Luo L. Composition operators on the Bloch space of several complex variables [J]. Acta Math Sin, 2000, 16:85-98.
[5] Ohno S, Zhao R H. Weighted composition operators on the Bloch space [J]. Bull Austral Math Soc, 2001, 63:177-185.
[6] Ohno S. Weighted composition operators betweenH∞and the Bloch space [J]. Taiwanese J Math , 2006, 5(3):555-563.
[7] Colonna F. Weighted composition operators betweenH∞and BMOA [J]. Bull Korean Math Soc, 2013, 50(1):185-200.
[8] 刘超,侯晓阳.Besov空间到Zygmund空间上的加权复合算子[J].纯粹数学与应用数学,2016,32(2):197-205.
[9] Stevic S. Weighted differentiation composition operators from mixed-norm spaces to weighted-type spaces [J]. App Math Comput, 2009, 211(1):222-233.
[10] Stevic S. Weighted differentiation composition operators fromH∞and Bloch spaces to nth weighted-type spaces on the unit disk [J]. App Math Comput, 2010, 216(2):3634-3641.
[11] 刘永民,于燕燕.从Hardy空间到Zygmund-型空间的加权微分复合算子[J].数学年刊A辑,2014,35(4):399-412.
[12] Liu J, Lou Z, Sharama A. Weighted differentiation composition operators to Bloch-type spaces [J]. Abstr Appl Anal,2013(1):233-255.
[13] Li S, Stevic S. Composition followed by differentiation between Bloch-type spaces [J]. J Comput Anal Appl, 2007,9(2):195-206.
[14] Zhu K. Bloch type spaces of analytic functions [J]. Rock Mou J Math, 1993, 23(3):1143-1177.
[15] Cowen C, Maccluer B. Composition operators on spaces of analytic functions [M]. Florida:CRC Press, 1995:128-129.

