关于均值不等式两个加强形式的注记

徐彦辉

(温州大学数理与电子信息工程学院，浙江温州 325035)

文[1]给出了均值不等式的两个加强命题.即：

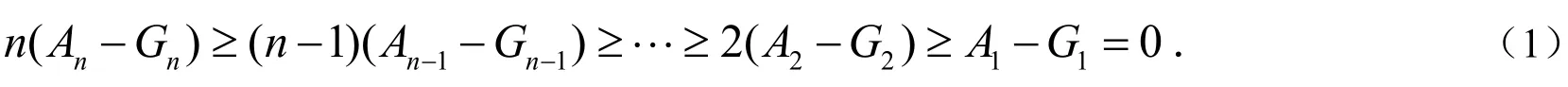
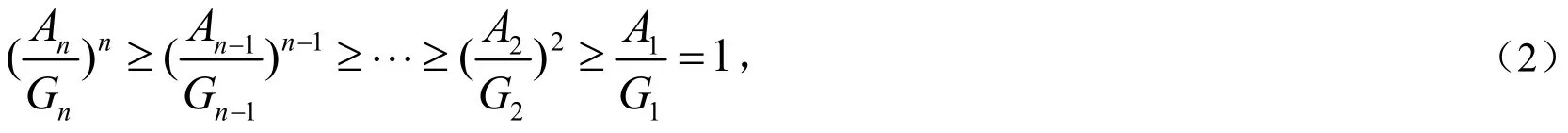
本文先给出这两个加强形式命题的一种简洁证法，然后，给出这两个加强形式命题的再加强命题.

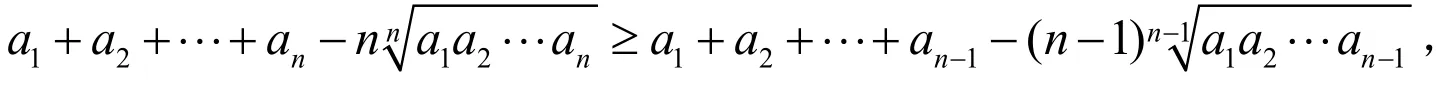
即只要证

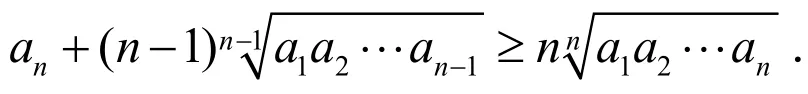
由均值不等式得

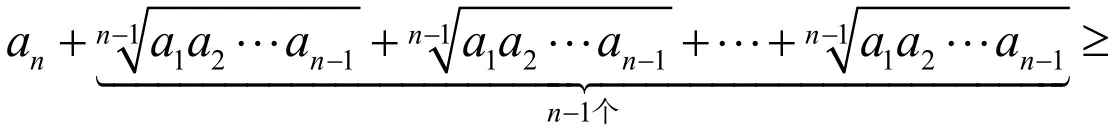
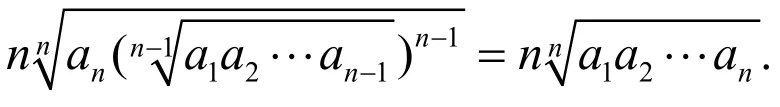
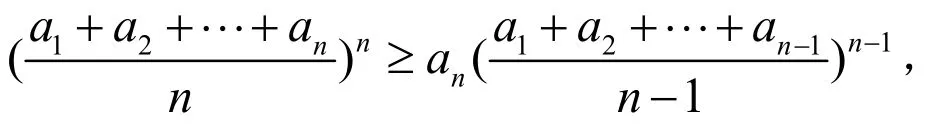
则

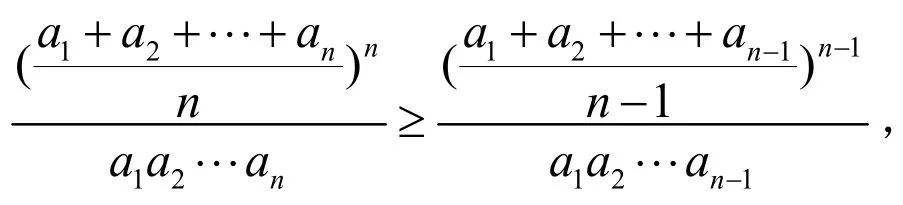
即

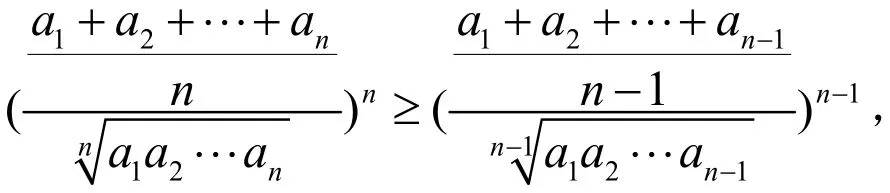
证毕.

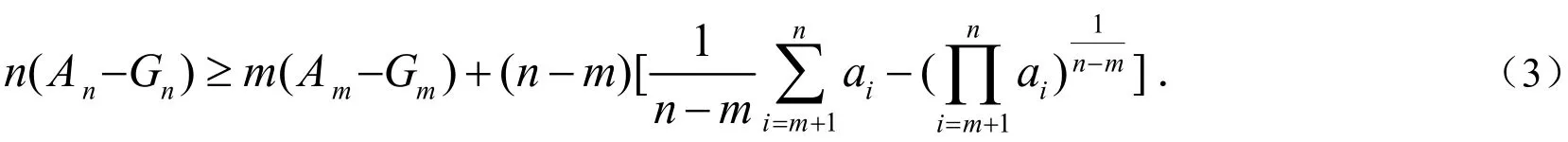
下面证明定理2，为此，先给出一个引理.

引理1[3]已知凸集，如果

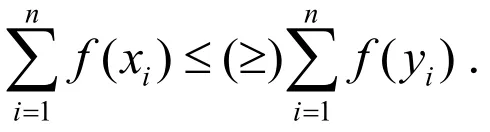
定理2的证明：先证(3)式，即只要证

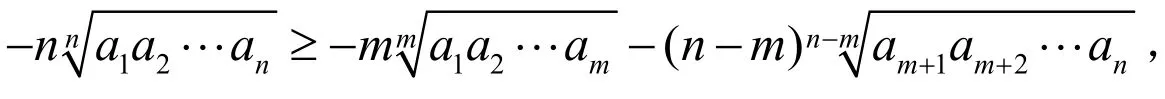
即只要证

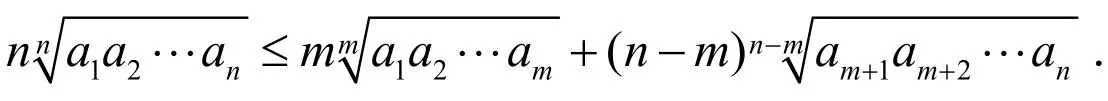
由均值不等式得

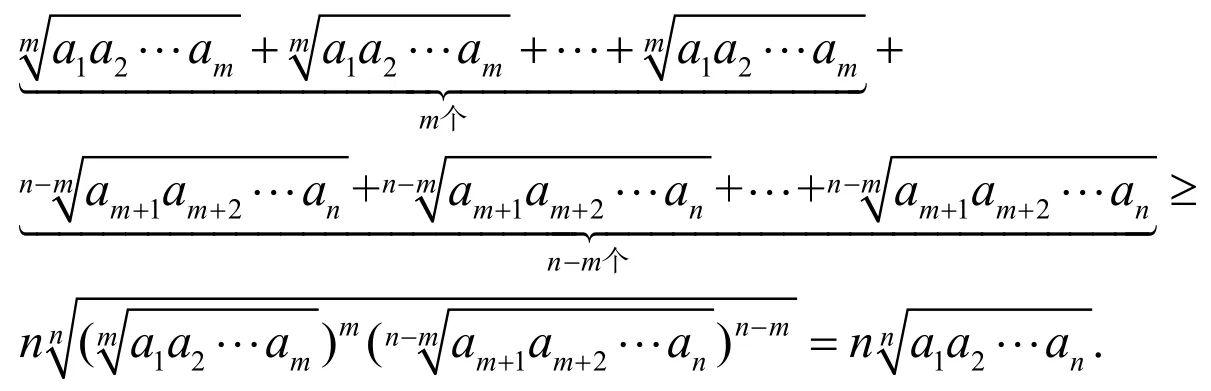
(3)式即得证.

再证(4)式，即只要证

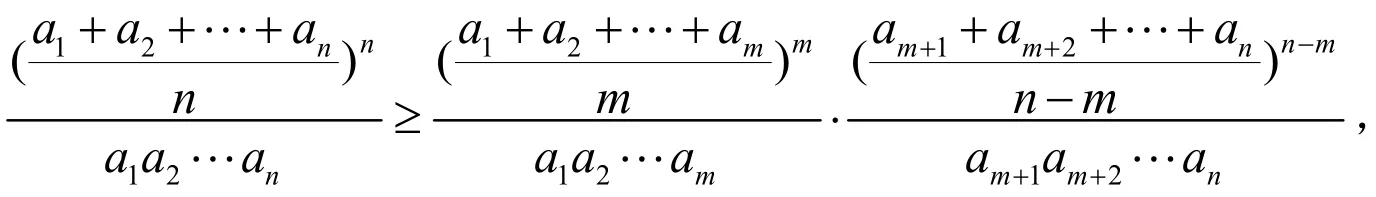
即只要证

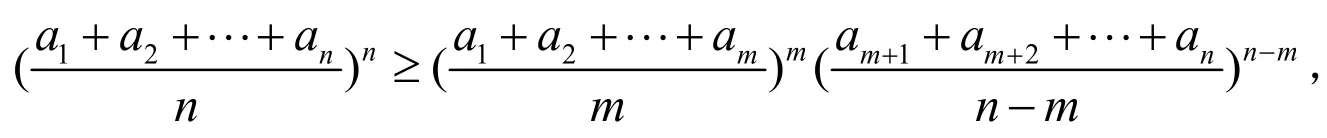
即只要证

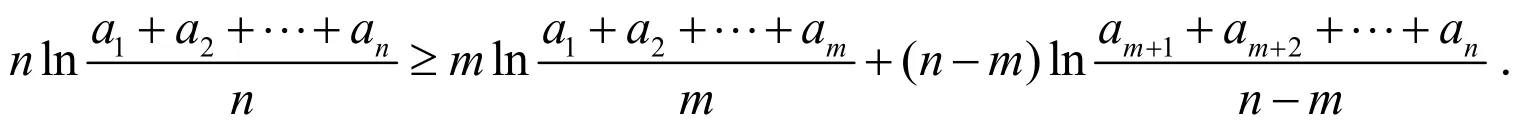
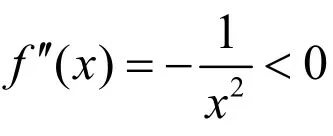
熟知，

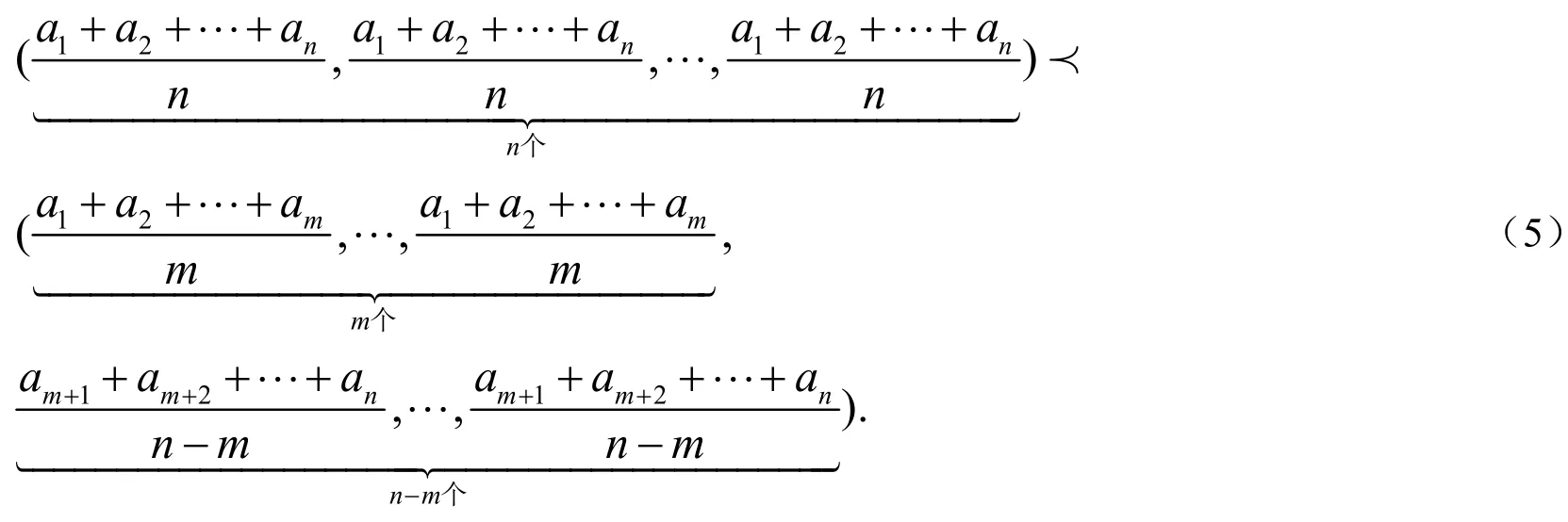
由(5)式和引理1即可得

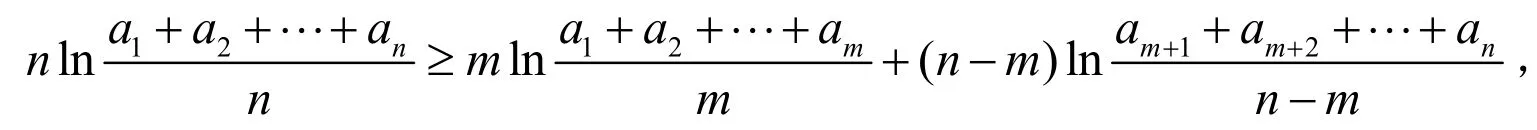
即

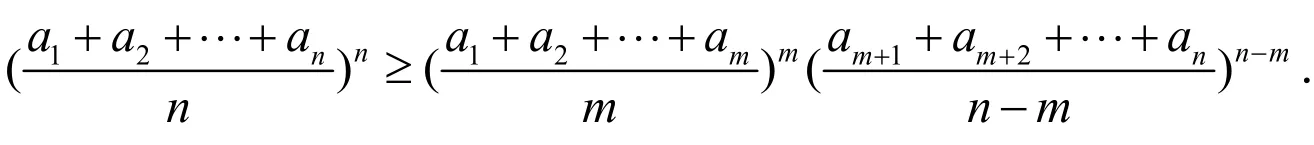
证毕.

[1] 蒋明斌，洪绍芳.加权平均不等式的加强[J].中学数学教学，1986(6)：194-195.

[2] 徐彦辉.均值不等式的两个加细及运用[J].温州大学学报(自然科学版)，2016，37(3)：1-5.

[3] 丁立刚，杨金林.关于Karamata不等式的一个证明[J].大学数学，2008，24(5)：149-152.