常系数三维椭圆边值问题的蒙特卡罗算法
柯李瑞
(温州大学数理与电子信息工程学院,浙江温州 325035)
在岩土工程、机械设计、弹性力学、材料力学等工程和物理问题中,常会遇到只需求解某几个特殊点处的函数值的集中载荷问题.这种情况下,继续使用有限元方法,会计算很多不必要的值,造成浪费.因此,文[1]提出了一种新的求解椭圆型方程的方法——有限元的概率算法,文[2]确立了有限元概率算法的基本理论,文[3]在此基础上针对一类特殊的二维椭圆边值问题提出了一种高效蒙特卡罗算法,使工作量大大减少.本文给出了一种求解常系数三维椭圆边值问题的蒙特卡罗算法,并通过算例说明了该方法的可行性.
1 一类椭圆边值问题的蒙特卡罗算法
问题的提出:

本文思路.首先,将方程(1)转化为如下方程:
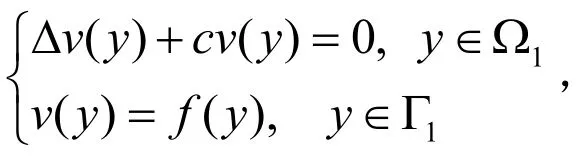
然后,运用有限元的蒙特卡罗算法求解上述方程即可.
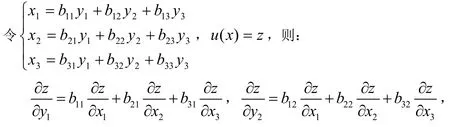

所以有:
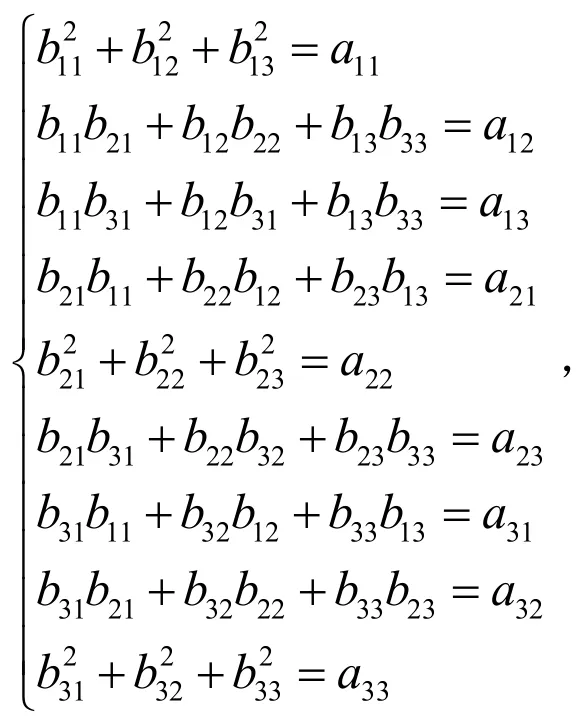
即BBT=A,其中
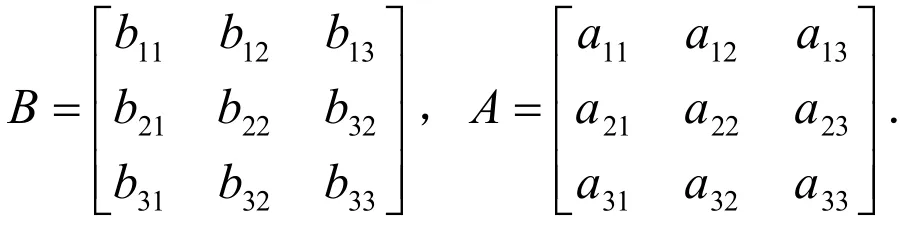
由A的对称正定性,可以求解得到.从而,方程(1)可以转化为如下形式:

求解方程(1)在任意一点数值解的问题转化为求解方程(2)在任意一点数值解的问题.
方程(2)是一类经典的方程,求解这类方程的关键在于Ω1和f(y),还有c.当Ω1,f(y)以及c中有一个改变时,方程的解也随之改变.
当Ω1为一般区域时,求解方程(2)的数值解比较困难.所以,本文先考虑简单情形:Ω1为以y0为球心,以R为半径的球.
设存在游粒β,当它位于点y时,质量为一单元的游粒拥有能量v(y).假设在初始状态下,处有一单位质量的游粒β,每次它都直接游动到Γ1,且游动到Γ1上的每一点的概率相同.记游到Γ1上的点为,则为随机变量[4],从而也为随机变量,关于有以下结论.
定理1[1]随机变量的期望与方差均存在,且
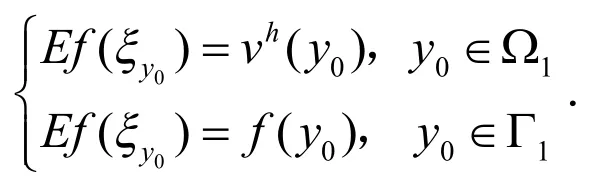

由以上分析可知,游粒游动到Γ1上的每一点的概率相同,所以可以构造如下求解的概率模型[5]:假设存在常数h>0.对边界Γ1进行三角形网格划分,以Ω1的内接正八面体为基础,将边界Γ1分为8个等球面三角形,然后应用“经纬度平分法”进一步细分球面三角形,直到Γ1上球面三角形的每两个顶点之间的距离不超过h为止.这样就得到边界Γ1的近似均匀划分.将网格顶点记为边界Γ1上的结点,且依次记为,令每次游动到的概率为:,这样构造的概率满足以下条件:
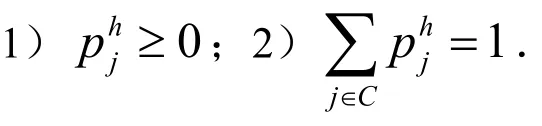
上面给出了当Ω1为以y0为球心的球时求解的方法.当Ω1为一般区域[6]时,由于计算困难,所以不使用游粒从y0直接到达Γ1上的方法来求,但可采用下述方法求:
取定一个足够小的数ε,在Ω1内以y0为球心,以y0到边界Γ1的最小距离为半径作球,并将其边界记为,半径记为R0.游粒从y0出发,直接随机游到,并且到达上的每一点的概率相同.记y0到达上的点为,有.由于未知,所以游粒需要继续游动.设y0到达上的点为y1,在Ω1内以y1为球心,以y1到边界Γ1的最小距离为半径作球,并将其边界记为,半径记为R1.游粒直接从y1出发,随机游到,并且到达上的每一点的概率相同.记y1到达上的点为,有.让游粒这样一直游动,若该游粒在游动ni次后到达Γ1,记该次实验终点为.如果在游动ni次后仍未到达边界Γ1,但到边界Γ1的距离小于或等于ε,不妨把它设为,让游粒直接游到边界Γ1上离它最近的点,记这次实验终点为.
设此次游动共进行了N次,由上述分析可得:

设实验次数为N,由以上分析,可得本文求解方程(2)的任意一点y0的数值解的蒙特卡罗算法的步骤如下:
1)取定N和ε;
2)取S=0;
3)取C=0;
4)取y=y0;
5)确定点y是否在Γ1上,如果点y在Γ1上,则转12),如果点y不在Γ1上,则转6);
6)求出y到Γ1的最小距离
8)以点y为球心,以Ri为半径作球,其中;
9)令y随机游动到Γi上任一点(游动到Γi上任一点的概率相同),记游动终点为yi,转5);
10)找到y距离Γ1最近的点,求出两点间距离,并让游粒直接到达该点;
13)判断C<N是否成立,若成立,转(4);
以上讨论了三维情况下求方程(2)在任意一点y0处的数值解的方法.由于本文要求的是方程(1)在指定点的数值解,所以首先应该将所求点x0转化为y0,然后用上述方法,通过求解y0处的数值解来得到x0处的数值解.
2 数值算例
考虑方程

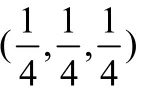
表1 点游动结果与方程精确解的比较Table 1 Comparison with the Result of the Equation at point and the Exact Solution of the Equation
通过上述算例,说明本文提出的对于常系数三维椭圆边值问题的蒙特卡罗算法是可行的.
[1] 朱起定.有限元概率算法[J].湘潭大学自然科学学报,1989,11(3):1-5.
[2] 朱起定.有限元概率算法的基本理论[J].湘潭大学自然科学学报,2001,23(2):121-133.
[3] 何文明,崔俊芝.一类特殊的椭圆型问题的高效蒙特卡罗算法[J].系统科学与数学,2004(2):210-217.
[4] 朱起定.椭圆边值问题的概率算法[J].系统科学与数学,2002(2):168-179.
[5] 孙文彬,赵学胜,高彦丽,等.球面似均匀格网的剖分方法及特征分析[J].地理与地理信息科学,2009(1):53-60.
[6] 朱起定.调和方程第一边值问题高效概率算法[J].计算数学,2000(1):121-128.
Monte-Carlo Method for Three-dimensional Elliptic Boundary Value Problem with Constant Coefficient

