二阶椭圆问题的修正Morley元方法

王文庆，汤 凯

(1.温州商学院基础部，浙江温州 325035；2.温州大学数理与电子信息工程学院，浙江温州 325035)

Morley元是常用于求解四阶椭圆型方程的一种非协调元，在每个单元上，它的形函数是完整的二次多项式，节点参数是单元顶点上的三个函数值及三边中点上的法向导数值.与传统的协调元相比，Morley元结构简单，是自由度最少的非协调元.1975年，Lascaux和Lesaint用严格的数学方法证明了Morley元对于四阶椭圆型问题的收敛性[1].而经过证明，Morley元对于二阶问题是发散的[2]，因此不能直接用于求解二阶椭圆问题.

本文通过引入投影算子，给出了一种求解二阶椭圆问题的修正Morley方法，并证明了其收敛性及低阶模估计.

1 修正的Morley元方法

问题(1)的变分形式为：

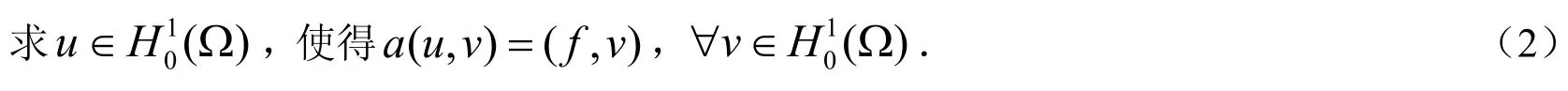
1)K是一个三角元；

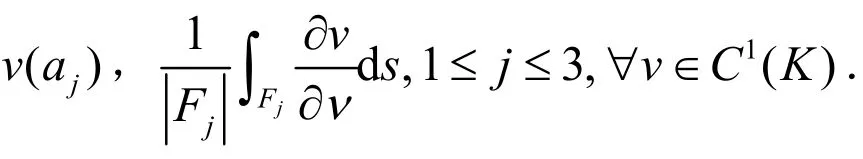
设

由上述定义可得：

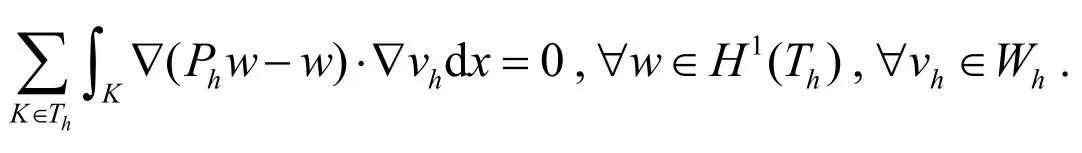
设Vh为函数值在Th外边界顶点处为零的Morley元空间，则二阶椭圆问题的修正Morley元方法就是求，使得

分别定义独立网格范数和半范如下：

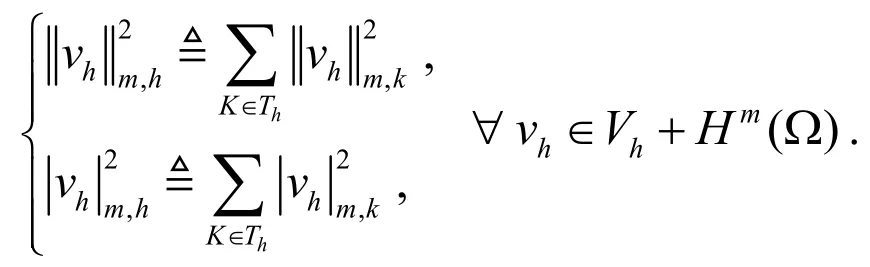
性质1 存在一个不依赖于h的正常数M＞0，使得

性质2 存在不依赖于h的正常数α，使得

2 误差估计

对离散问题(4)的修正Morley元解uh进行误差分析.在下面的证明中，C表示一个与网格大小及函数无关的常数，在不同的地方出现可以取不同的值.

现给出以下引理：

证明：由投影算子hP定义可得：

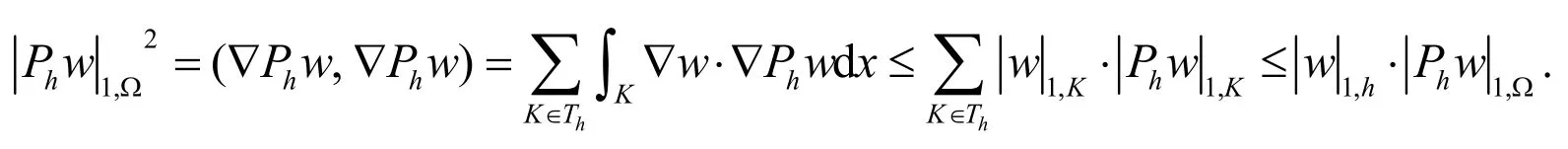
则有

证毕.

定理1 设u和uh分别为问题(2)和(4)的解，且，则

证明：设uI是u在Vh上的插值，是u在Wh上的插值.令，则

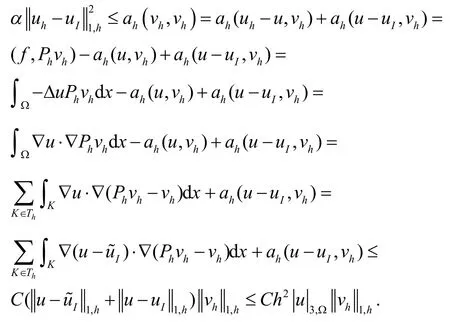
所以有：

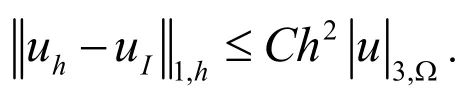
由三角不等式得：

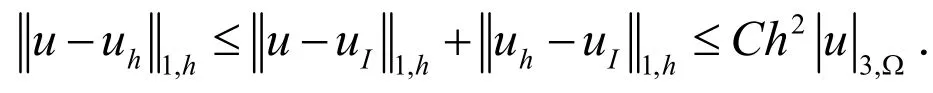
证毕.

定理2 设u和uh分别为问题(2)和(4)的解，为有界凸多边形区域，且，则有：

证明：设w为如下辅助变分问题的解：

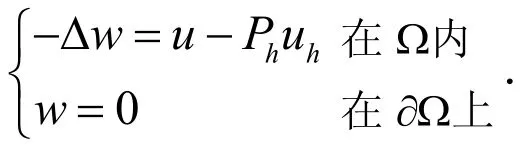
在凸多边形区域的假设下，有正则性估计[5]：

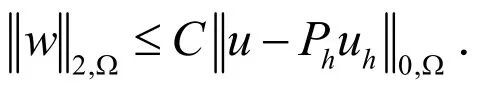
设wI是w在Vh上的插值，是w在Wh上的插值.

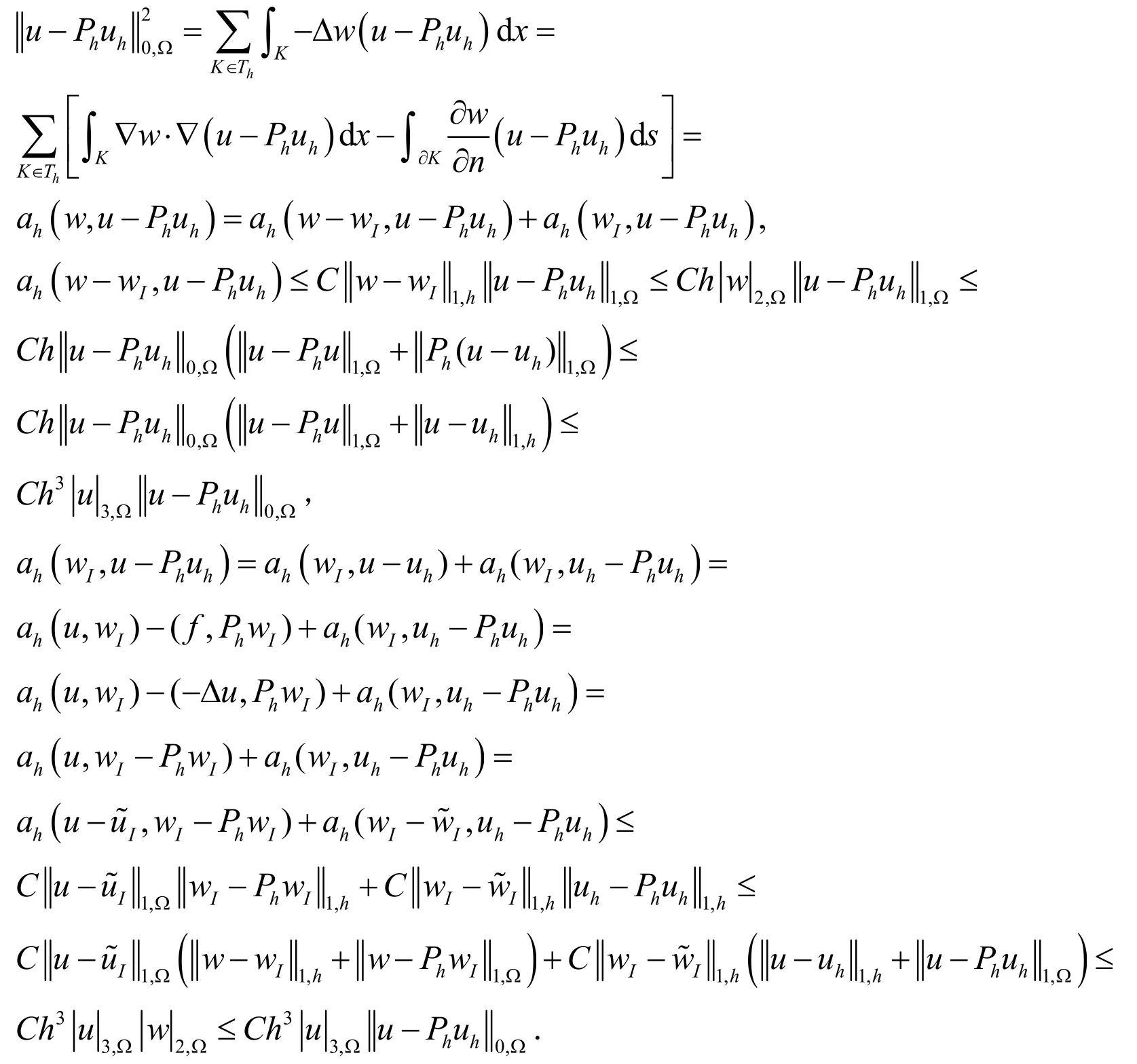
所以有：

证毕.

[1] Lascaux P, Lesaint P. Some nonconforming finite elements for the plate bending problem [J]. Rairo Anal Numer, 1975,9(1):9-53.

[2] Wang M. On the necessity and sufficiency of the patch test for convergence of nonconforming finite elements [J].Siam J Numer Anal, 2001, 39(2):363-384.

[3] Wang M, Xu J C. The Morley element for fourth order elliptic equations in any dimensions [J]. Numer Math, 2006,103(1):155-169.

[4] Wang M, Xu J C, Hu Y C. Modified Morley element method for a fourth order elliptic singular perturbation problem[J]. J Comput Math, 2006, 24(2):113-120.

[5] Ciarlet P G. The finite element method for elliptic problems [M]. North-Holland:North-Holland Publishing Co. , 1978:131-139.