平面曲线上的几何性质——等周不等式及距离比较定理的初等证明

何明旺

(温州大学数理与电子信息工程学院，浙江温州 325035)

考虑平面正则曲线[1]

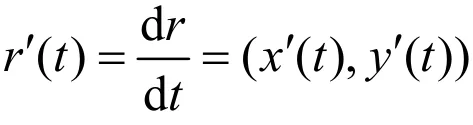
通常将s称为曲线的弧长参数.对于正则曲线r，我们总可以取它的弧长作为参数来表示.在弧长参数下，有

即曲线r(s)的切向量长度为常值1.我们用来表示 (s),y(s)x对参数s求导的量，比如.通常将单位向量(s)记为t(s).从几何学的角度来讲，是曲线在点的单位切向量.另外规定曲线称为正则曲线，如果：

注意到t(s)是的法向量，且与曲线r相切.与t(s)垂直的向量称为曲线r在点的法向量.选取一个单位法向量n(s)与t(s)垂直，构成正交坐标系，且这个坐标系与{i,j}定向相同是右手系).称n(s)是曲线r(s)在点的单位正法向量，它由t(s)唯一确定.

一般的，沿曲线r(s)，有单位切向量t(s)和单位法向量是一个以r(s)为原点的正交标架.这时候曲线r(s)上任何一点都有一个这样的标架，称为沿曲线r的Frenet标架[1].可以得到它们之间存在这样的关系：

由(8)式(9)式确定的一个函数κ(s)称为曲线r(s)的曲率.

定理1设A是一条长为L的平面单纯正则闭曲线C所围成的面积，则有如下不等式：，式中等号当且仅当C是圆时成立.

定理2 平面内两条曲线g和f它们的长度为定值L(以弧长s为参数)，它们的曲率不同，那么两条曲线g和f两端点之间的距离Dist不同，两条曲线对应曲率大的那条曲线的两端点之间的距离Dist要小.

1 定理1的证明

证明：根据格林公式[2]

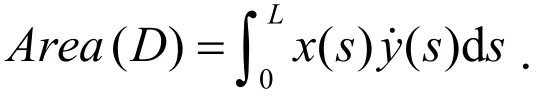
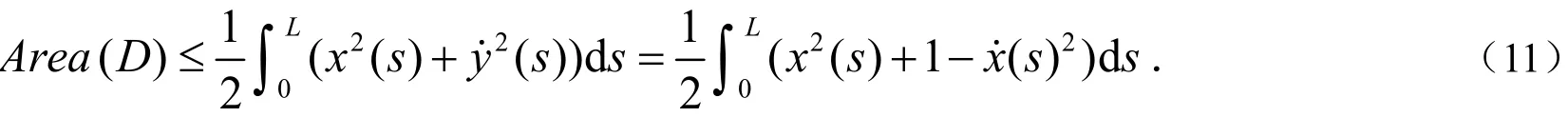
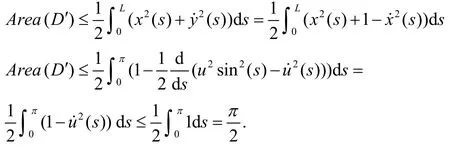
所以

若“=”成立，由(13)式可知u(s)≡常数C.

也就是当“=”成立，平面正则曲线是一个圆.

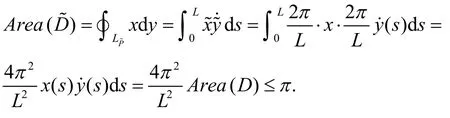
所以

定理1得证.

2 定理2的证明

设两条曲线g和f它们的长度为L(以弧长s为参数)，它们的两个端点分别记为A,B和C,D.在平面内建立一个平面直角坐标系，AB和CD都与x轴重合.

规定gθ和fθ分别为曲线g和f的某一点的切向角[4]，并且在曲线g上存在一点s0，使在该点的切线平行于x轴[5]，即，且

那么根据(18)式可知，存在一点s0使得.那么

所以定理2得证.

[1] 彭家贵，陈卿.微分几何[M].北京：高等教育出版社.2002：14-21.

[2] 华东师范大学数学系.数学分析[M].上海：高等教育出版.2008：148-154.

[3] Guo H X, Philipowski R, Thalmaier A. An entropy formula for the dependent metric application to ancient solutions[J]. Pac J Math, 2013, 264 :61-82.

[4] Hamiltion R. Remarks on the entropy and Hamack estimates for the Gauss curvature flow [J]. Commun Anal &Geom,1994, 2(1):155-165.

[5] 陈省身，陈维恒.微分几何讲义[M].2版.北京：北京大学出版社，2004：331-335.

[6] Huisken G. Contracting convex hypersurfaces in Riemannian manifolds by their mean curvature [J]. Invent Math,1986, 84:463-480.