浅谈系统化变式教学在中考数学复习中的运用

广东省汕头市聿怀初级中学(515041) 李惜珠

系统化变式教学,是指教师在教学过程中,根据学生所处学段的相关知识和方法进行变式,通过对命题进行变式、整理、比较,从而产生新的情景、问题,诱发学生从不同角度,不同方法去思考解决问题,强化发散思想,培养创新能力的教学方法.复习课中运用系统化变式教学对问题进行更新,重组,使其本质不断升华,从而达到举一反三,融会贯通的效果.它通过变式循序渐进地揭示某一问题所涉及的知识、方法、思想之间的内在联系,使学生对某一问题达到深刻理解的程度,储存更持久,提取更快捷,因此系统化变式教学符合脑科学的原理.

根据中考数学复习的特点,系统地运用变式教学方法就是将“点-线-面”的变式教学结合起来.中考复习过程主要分为习题(例题)课,专题复习课,套卷(测试)讲评课.

(1)系统化变式教学在习题(例题)课中的运用

数学能力的提高离不开解题,可是题海战术却大大地增加学生的负担,难以培养思维能力,所以教师在教学中应该追求“效能”而非“数量”,而习题的变式教学无疑是一剂良方,它将习题例题进行变式,最大可能地覆盖所学知识点,把分散的知识点串成一条线,从一个思维含量较少的题目出发,逐步进行变式,每一次的变化都转向学生知识技能的最近发展区,激发学生探索热情,帮助学生梳理知识之间的内在联系,提高学生对知识的综合运用能力.例如在相似三角形的复习中,教师讲解了如下例题:

例1如图1,在等边△ABC中,P为BC上一点,D为AC上一点,求△ABC的边长.

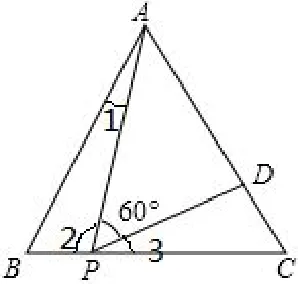
图1

解 设△ABC的边长为x,则PC=x-1.因为∠APD=60◦,所以 ∠2+ ∠3=180◦-60◦=120◦. 因为在等边 △ABC中,∠B= ∠C=60◦.所以在 △ABP中,∠1+ ∠2=180◦-60◦=120◦,所以 ∠1= ∠3,所以

例题讲解后,教师给出了变式练习.

例2 如图2,在等腰△ABC 中,∠BAC = 90◦,AB=AC=1,点P是BC边上的一个动点 (不与B、C重合),在AC上取一点D,使∠APD=45◦.

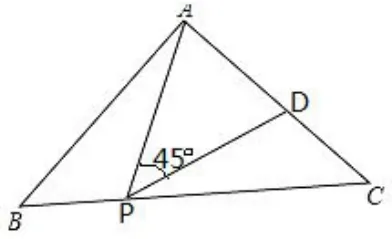
图2

(1)求证:△ABP～△PCE;

(2)设BP=x,AD=y,求y关于x的函数关系式及自变量x的取值范围,并求出当BP为何值时AD取得最小值?

学生在刚才例题学习的基础上,看到类似的习题会兴趣提高,主动性增强.因此,习题课教学活动中采用变式教学,教师科学的问题,进行循序渐进的变化,创设问题情景,不仅可以激发学生的学习热情,巩固所学知识,而且可以使得学生思维更加广阔,分析问题和解决问题的能力也得到提高.充分发挥习题例题的变式教学功能,给学生提供自主探究的机会,让他们经历“再发现再创新”的过程,培养学生的创新意识,不仅提高了成绩,也获得终身学习的能力.

(2)系统化变式教学在专题复习课中的运用

专题复习课是初三数学总复习中的重要阶段,它是以综合运用为中心,以解题能力和优化思维品质为目的的复习阶段,而系统变式教学恰好是数学专题复习的一种基本模式.近年来中考数学考试中难度较大或中等难度的题目多数取材于教材中的例题或习题,但又在此基础上加强或减弱条件,延伸或拓展而成的.因此数学专题的复习要在教材的基础上,通过变解法,变条件,变结论等,多角度进行变式教学.

例如,在一元二次方程面积应用题的专题复习中,教师由课本习题引入,题目如下:

例3 如图3,利用一面墙(墙的长度不限),用20m长的篱笆,怎样围成一个面积为50m2的矩形场地?

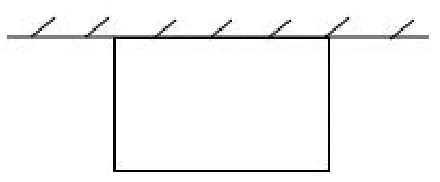
图3

学生感觉题目简单,很快地就给出解答过程:

答:所围成的矩形菜园的一边长为10m,另一边长为5m.

教师紧接着追问:能围成面积是60m2的矩形场地吗?

显然,教师的这一问题的提出既能再次巩固学生对问题的理解,也复习一元二次方程无实数根的情况.

解答完该问题后教师又抛出了另一问题:

例4 如图4,如果在矩形场地内部再围一篱笆,那么怎样围成一个面积为25m2的矩形场地?=25,解得:x1=15,x2=5,所以

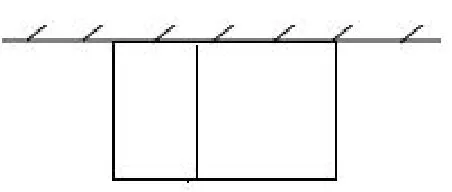
图4

(有学生马上举手了)或5.

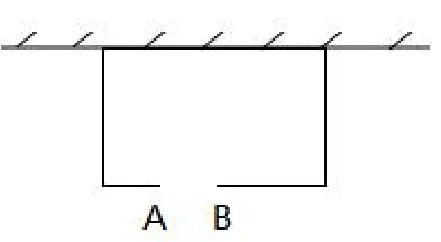
图5

因此,在专题复习中,老师善于对题目的条件加强或减弱,对问题延伸或拓展,不仅能大大提高学生学习的积极性,而且能够起到事半功倍的效果.

(3)系统化变式教学在套卷(测试)讲评课中的运用

试卷讲评是教学的补充拓展与改进的基本措施,也是对学生再进行解题指导总结的基本途径.在试卷分析讲评中,我们总能发现一些练习册中已经做了也评讲了的题目,稍微经过“变形”后,学生就不能很好地完成,这说明学生的知识迁移能力还是比较差.因此,在试卷讲评课中运用变式教学,将考点拓展,深化,增加难度,或引导学生进行一题多解,一题多变等训练,让学生在试卷讲评中有所发现,有所提高,这对知识的迁移,规律的总结都有较大的帮助,从而使学生提高解决问题的能力.

例如教师在讲评考卷中的题目:

例6(2015.浙江宁波)已知抛物线y=(x-m)2-(xm),其中m是常数.

(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;

○1求该抛物线的函数解析式;○2把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点?

大部分学生的解法如下:

(1)证明:y=(x-m)2-(x-m)=x2-(2m+1)x+m2+m,因为Δ =(2m+1)2-4(m2+m)=1＞ 0,所以不论m为何值,该抛物线与x轴一定有两个公共点.

jieba 分词一个Python 中文分词组件，使用前缀词典的词图扫描，支持精确、全模式、搜索引擎三种分词模式，取全切分后最大概率路径的切分方案，将未登录词的分词视为序列标注的问题，用HMM 模型进行识别。

○2该抛线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为y=x2-5x+6+k,所以Δ =52-4(6+k)=0,所以即把该抛物线沿y轴向上平移个k=单位长度后,得到的抛物线与x轴只有一个公共点.

评讲完常规的解法后,教师引导学生将二次函数与一元二次方程相结合,学生经过思考,整理,又得出另一种解法:

(1)证明:因为y=(x-m)2-(x-m)=(x-m)(xm-1),所以当y=0时,(x-m)(x-m-1)=0,解得x1=m,x2=m+1.因为m/=m+1,所以不论m为何值,该抛物线与x轴一定有两个公共点.

因此,一题多解,一题多变的训练,能够让学生在较短时间里巩固掌握更多的知识点,为中考复习赢得宝贵的时间.

系统化变式教学能使学生多角度理解知识的来龙去脉,形成知识网络,使学生抓住问题的本质,加深对问题的理解.因此,变式教学是对学生进行数学技能和思维训练的重要方式.在中考复习教学中,我们通过对数学问题进行多角度,多方向的变式探究,有意识地引导学生从“变”的现象中发现“不变”的本质,从“不变”的本质中探索“变”的规律.系统化变式教学能够将各个知识点串联起来,用横向、纵向、逆向思维训练,这不仅能增强学生的创新意识和应变能力,而且能优化学生的思维品质,提高拓展学生创新思维、培养发现问题和解决问题的能力和素养.