由一道单元测试题引发的思考

广东省仁化县仁化中学(512300) 金海兵

一、问题提出

在学习完必修5第一章正、余弦定理后进行了一次单元测试,其中一题的讲评引发了笔者的思考,现将讲评过程中的师生对话摘录如下:

由于难度不大,请生1回答解题思路.

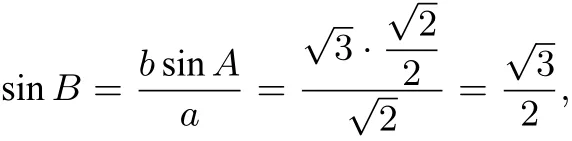
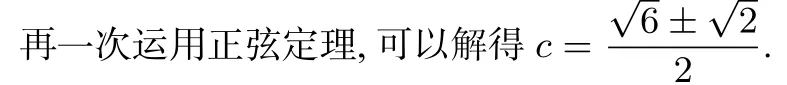
师:你是如何想到用正弦定理的?

生1:此前已经总结过条件中含两边及一边的对角或两角一边时用正弦定理.

生2:直接使用余弦定理可快速求出:

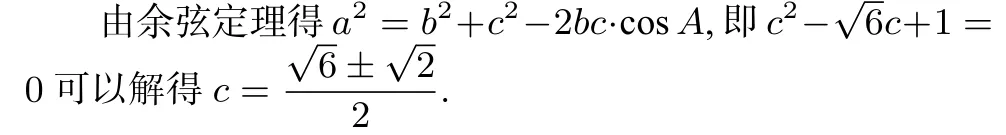
师:你是如何想到使用余弦定理的?

生2:教辅书中有类试题型.

师:对生2的自学能力表示赞赏,我们能从此题中总结出此类问题的解法吗?

生3:已知两边及一边的对角解三角形正、余弦定理均可使用.

此时生4提出了疑惑:此处的结论似乎让之前已经总结的结论变得混乱,如已知三边或两边及夹角用余弦定理解,能用正弦定理吗?

突如其来的提问打乱了原有的教学设计,一直都要求学生牢记正、余弦定理各自使用的题型,解题过程中对号入座,而对定理之间的关系及能解决的题型未做深层次的思考,课后笔者针对此问题做了进一步的思考.

二、问题的思考

思考一 已知两角一边的情况能否用余弦定理解决?

以上解法可以推广到一般情况.

思考二 已知两边及夹角的情况能否用余正弦定理解决?

以上解法可以推广到一般情况.

思考三 已知三边能否用正弦定理解三角形?

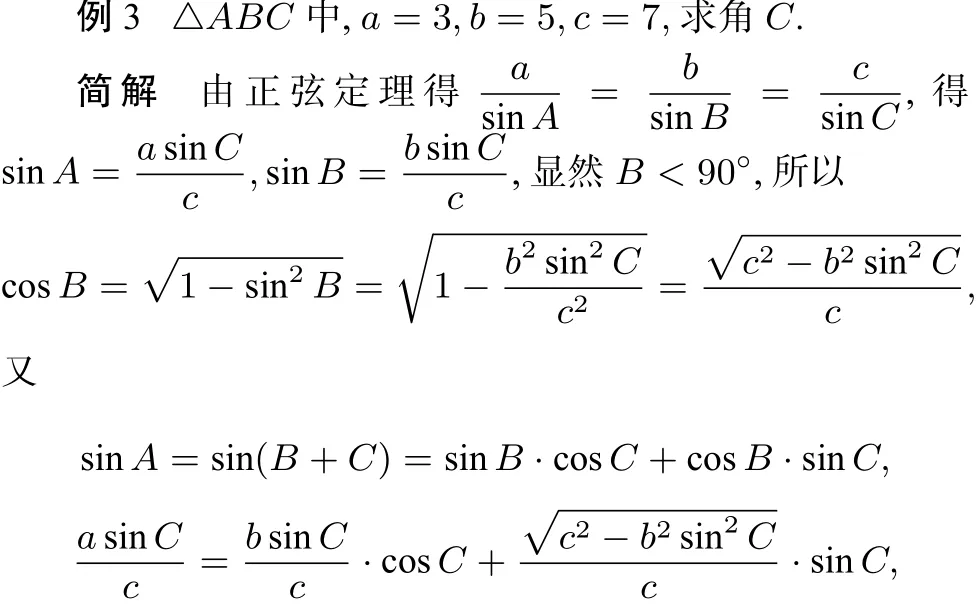
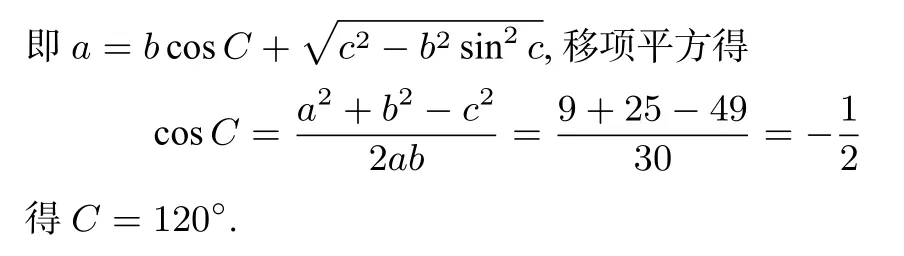
2、由余弦定理推导正弦定理:

以上解法可以推广到一般情况.

综上可以发现:教学中所总结的已知两角一边、两边及一边对角用正弦定理,已知三边、两边及夹角用余弦定理,只是针对特定题型提出的最简单方法,便于学生快速解题,事实上四种题型都可以通过单独一个定理来解决.

思考4 通过上述思考可以发现,能用正弦定理解决的问题同样能用余弦定理解决,同样的能用余弦定理解决的问题也能用正弦定理来解决,区别在于步骤的多少及计算的繁杂程度,也就是说,正、余弦定理本质上并没有区别,只是表示的形式有所不同,笔者通过推导及查找相关资料,得到了正余弦定理的等价性证明.

同理可证:

三、点滴体会

数学学习强调探究,通过多方位、多角度、多途径观察和解决问题,能够激发学生学习数学的热情,能够进一步增强学生对数学基本概念基本定理的理解,能够提高学生处理问题的能力,能够指引我们发现问题、定理的内在联系,因此在平时学习数学的过程中,要善于多角度、全方位地分析与思考问题,以达到拓宽思路、发展创新思维的目的.随着广东高考使用全国卷,对于学生的思维能力有了较高的要求,所以教学中再按照以前的一个定理三点注意进行只会把知识教死,不利于学生思维的拓展,教师要以此为契机加强自身业务水平的钻研,加深对定理的理解,把知识教活,学生才会变通,相信只要学生能抓住了定义、定理的本质,无论是考广东卷还是全国卷都能取得优异成绩.