“要是先知道定值是多少就好了”—如何确定圆锥曲线“定值问题”中的定值

上海市民办交大南洋中学(201504) 李丽娜

圆锥曲线是历年高考试题的热点问题,其中客观题主要考察离心率和双曲线特有的渐近线的一些简单知识,而主观题经常以压轴题的形式出现,考察知识全面,系统,而且计算量比较大,得分比较困难.历年高考压轴题中对圆锥曲线的考察大体可以归纳为如下四个部分:方程(轨迹)问题,最值(取值范围)问题,定值(定点)问题,“是否存在”问题.本文就定值问题中的直接证明某个量为定值的问题(不包含是否为定值的问题)作点简单的说明.在教学过程中,笔者常常听到学生说“要是先知道定值是多少就好了?也好确定自己算的对不对.”,下面通过几个典型的高考压轴题,就如何通过一些特殊的方式先来确定‘定值’是多少,好做到心中有数,浅谈一下自己在教学过程中的做法.

例1 (2011四川理21)椭圆有两定点A(-1,0),B(1,0),过其焦点F(1,0)的直线l与椭圆交于C,D两点,并与x轴交于点P.直线AC与直线BD交于点Q.

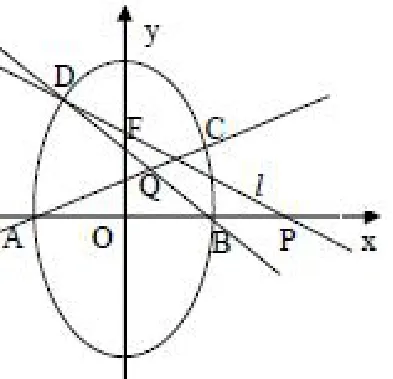
图1

分析 主要分析下第(2)问:解决此类问题一般是先通过题目中的一些特殊的点,线位置关系来先确定定值是多少,然后再通过详细的计算或推理加以严格的证明.点决定线的位置,于是解决问题的关键就是先去寻找特殊的点.特殊的点一般具有如下特征:比如圆锥曲线与坐标轴的交点,当然点的选取首先要保证计算简单,如果选的点不当的话,计算量会非常大,这就与我们最初的目的背道而驰了.

通过第二问的题干,我们可以明显的感觉到特殊的点应该是A,B,为什么会有这样的感觉,那就是命题人为什么把这两个点给排除了?是两个点对于题干的设问比较简单(易于计算),还是两个点在题干所叙述的情况下没有意义呢?下面我们来分析一下这两个点:

以点P与B重合为例:此时D点肯定不与B重合(如果重合,直线BD不存在),而C,Q与点B重合,可见此时这种情况在题干叙述的情况下是存在的,有意义的.我们很容易就可以得到这种情况下,这样我们就得到了这个定值.

在大题中再通过推理或计算验证就可以了,如果在选择或填空中出现这样的题目,可以起到事倍功半的效果.

同理可以验证P与A重合的情况,在此不再多说.

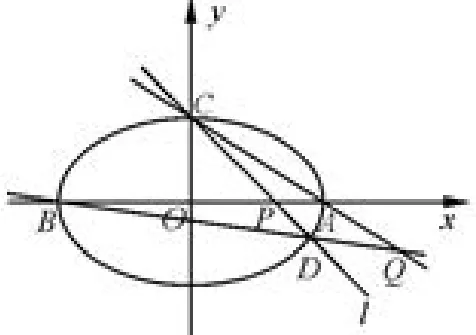
图2

分析 通过题干P异于B点,我们很明显的可以感觉到此题中P与A点重合是可以的,可见这就是我们要寻找的特殊的位置关系,显然此时D,Q与点A也重合了,只有这样,题干所叙述的情况才会出现.因此可以得到

上述两个例题的详细解法可以参考高考试题的参考答案所提供的解题过程.

(1)求椭圆C的方程;

(2)E,F是椭圆上C的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明:直线EF的斜率为定值,并求出这个定值.

分析 主要分析第(2)问:题干中的关键是直线AE的斜率与AF的斜率互为相反数,这句话说明直线AE,AF与x轴的交点和过点A,且与x轴垂直的直线是对称的.此时可以考虑特殊的位置,让点F与椭圆的右顶点重合,根据上述分析,结合椭圆的方程(半长轴为4),(直线AE)必过原点,根据对称关系,可以求得E的坐标为从而.此题的详细解法可以参考高考试题的参考答案所提供的解题过程,下面提供此命题的一个推广:

设A(x0,y0)是椭圆=1(a＞b＞0)上的一个定点,E,F是椭圆上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明:直线EF的斜率为定值,并求出这个定值.

我们还可以在双曲线和抛物线中得到类似的结论,类似的题目在高考试题中还有2004年北京卷理科的17题和2005年江西卷文科的22题,此次不再说明.

最后,显然通过上述方法得到的定值需要进行严格的证明,但在考试过程中可以让学生做到心中有数,来确定自己最后的计算是否正确.在选择或填空中,通过点的特殊的位置关系来确定定值,可以节约考试时间,起到很好的效果.类似的题目在高考中还是比较多的,比如2007年重庆理科的压轴题.