七年级数学教学中渗透数学思想方法策略初探

广东省广州市新滘中学(510320) 汪小燕

数学思想方法是数学学科的精髓,是学生将获取的知识转化为数学能力的纽带.七年级是小学与初中的衔接阶段,根据新课标精神、七年级的知识内容和学生的实际,主要渗透的数学思想方法是:消元法、换元法、类比归纳、整体思想、数形结合的思想、方程的思想、分类的思想、转化的思想.

教学实践证明,数学思想方法比数学知识更为重要,这是因为:数学知识是定型的,静态的,而思想方法则是发展的,动态的.知识的记忆是暂时的,思想方法的掌握是永久的.知识只能使学生受益于一时,思想方法将使学生受益于终生.培养初中生的数学思想方法,可以有效地激发学生的学习兴趣,充分调动了学生学习积极性和主动性,能使学生的认知结构不断地完善和发展,使学生将已有的思想方法运用在学习新知识的过程中,能够把复杂问题转化为简单问题来解决,提高学习效益,提高学生分析问题和解决问题的能力.

1.渗透数学思想方法策略

七年级数学是从小学的数字语言到初中的符号语言的过渡阶段,数学思想方法的渗透是教学的难点,隐性地存在于知识点的教学中.数学教师必须从学生的最近发展区出发,设计合理的教学策略.

1.1 知识主线,挖掘思想

七年级数学教材中处处渗透着基本数学思想方法,数学概念、公式、定理等知识写在教材中,是有“形”的,而基本的数学思想方法在教材中是无“形”的.它以隐藏的形式存在于字里行间,并且不成体系散见于教材各章节之中.教师要抓住各种时机,引导学生观察、归纳、总结出蕴含的思想方法.

例1 已知点A,B,C在同一直线上,线段AB=8cm,线段BC=2cm,M是线段AC的中点,求AM的长.

解析 由于点C可能在点B的左侧或右侧,所以要分两类情况,可求得AM的长分别是5cm或3cm.

点评 此题是《几何图形初步》章节的一道题,但挖掘其中的数学思想就是分类的思想.在以知识为主线的教学中,教师要不失时机的渗透数学思想,并及时指出思想方法的内涵.如有理数分为整数和分数,|a|去掉绝对值符号分为三种情况,蕴含的就是分类的思想;绝对值的几何意义蕴含的就是数形结合的思想;从几个特殊情况找出一般情况的规律蕴含的就是归纳的思想.教师若只重视讲授表层知识,而不注重渗透数学思方法,学生的知识水平永远停留在一个初级阶段;反之,如果单纯强调数学思想和方法,而忽略表层知识的教学,就会使教学成为无源之水,学生也难以领略深层知识的真谛.

1.2 分析透彻,抓住本质

数学思想方法的渗透,不是在于教师讲过多少次与思想方法有关的题目,关键在于教师要把握时机,将知识内涵要分析透彻,抓住渗透的思想方法本质,促进学生悟出蕴含的数学思想方法.

例2 已知代数式ax5+bx3+3x+c,当x=0时,该代数式的值为-1.

(1)求c的值;

(2)已知当x=1时,该代数式的值为-1,试求a+b+c的值;

(3)已知当x=3时,该代数式的值为9,试求当x=-3时该代数式的值.

解析 (1)把x=0代入代数式,得到c=-1;

(2)把x=1代入代数式,得到a+b+3+c=-1,则a+b+c=-4;

(3)把x=3代入代数式,得到35a+33b+3×3+c=-1,35a+33b=-1+1-9=-9;当x=-3时,

原式=(-3)5a+(-3)3b+3×(-3)+c=-(35a+33b)-9-1=-(-9)-9-1=-1.

点评 此题表面上是一道整式求值的题目,如果教师只是按部就班的分析答案,似乎可以完成教学任务.但是问题的本质并没有抓住,下次遇到类似的题目,有些学生看到求a+b+c,以为必须知道a,b,c三个字母的取值,从而认为条件不足此题没法求解.其实第二问和第三问都体现了整体的思想,教师要不失时机的挖掘其中的内涵.为了七年级学生更易于理解整体代换思想,可以将第三问的式子‘‘35a+33b”用“△”代替,那么目标明显就是“-△-9-1”.此题也是七年级学生从“数字”到“字母”的一次飞跃,渗透的整体思想,对于提高学生的符号感是很有好处的.

1.3 反复渗透,螺旋上升

数学思想方法的学习一般分为三个阶段:模仿阶段,初步应用阶段,自觉应用阶段.学生对各种数学思想方法的认知都是在反复理解和运用中形成的,有一个低级到高级的螺旋上升过程,对同一数学思想方法,应该注意在不同知识阶段的再现,日积月累的强化,学生才有可能悟出思想方法的妙处并自觉运用.

比如《一元一次方程》这一章节,从知识角度主要是学习如何解一元一次方程以及用一元一次方程解决相关应用题,从思想方法的角度是渗透了方程的思想.但是在后续教学中发现,学生利用方程思想解决问题的主动性不强,说明不是学完“方程”就知方程思想的内涵.

例3 如图1,BD平分∠ABC,BE分∠ABC为2:5两部分,∠DBE=21◦,求 ∠ABC的度数.

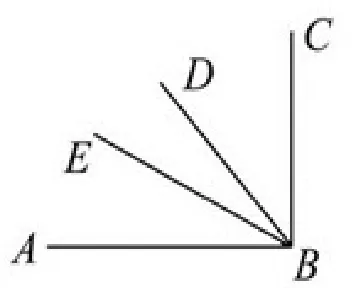
图1

解析 因为BD平分∠ABC,所以 ∠ABD= ∠CBD,因为BE 分 ∠ABC 为 2:5两部分,设 ∠ABE=2x◦,则∠EBC=5x◦,∠ABC=7x◦,因为 ∠DBE=21◦,所以2x+21=5x-21,解得x=14,所以∠ABC=14◦×7=98◦.

点评 本题以BE分∠ABC为2:5两部分引出未知数x,以∠ABD和∠CBD相等建立等量关系,也就是主动利用方程求出x,最终求出目标角∠ABC.本题出现在《几何图形》章节中,而方程的思想是前一章节渗透的内容,教师要有反复渗透的理念,那么思想方法的螺旋上升才有机会得以实现.

1.4 变式教学,思维灵活

在教学中,有的学生表现思维灵活,能迅速洞察问题本质,解决问题有独创性.而有的学生则反应迟钝,思路狭窄,只习惯于做熟悉的题目,而问题背景发生一点变化就会手忙脚乱,更不用谈主动利用数学思想方法解题.教学中教师可不断变换问题呈现的方式,通过“一题多解”、“一题多变”、“题组辩误”等变式途径,发散学生思维,对学生更加深刻、灵活的掌握数学思想方法是有好处的.

例4 如图2,已知 ∠AOB=90◦, ∠BOC = 30◦,OM 平 分∠AOC,ON 平 分 ∠BOC, 求∠MON的度数.

解析 因为OM,ON分别平分∠AOC,∠BOC,

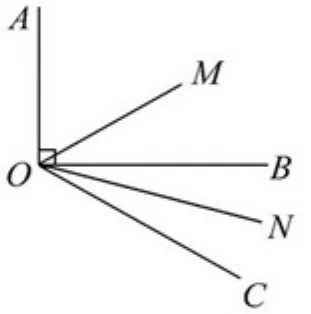
图1

因为∠AOB=90,所以

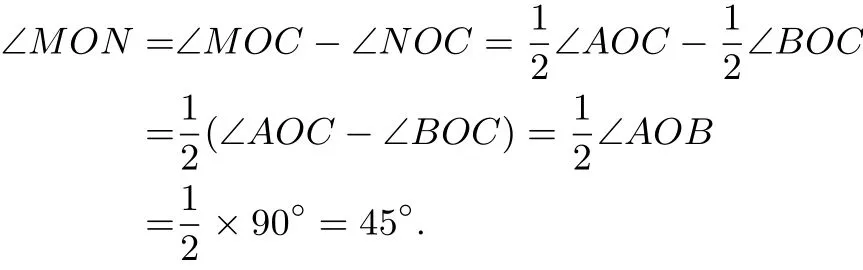
点评 本题将“复杂问题”转化为“简单问题”,体现的是转化的数学思想,目标角∠MON直接求解很困难,但是通过分解为∠MOC与∠NOC的差,再利用OM,ON分别平分∠AOC,∠BOC,将目标角最终转化为∠AOB的一半,即求出结果为45◦.但是转化的思想的渗透,通过一个例题还不够到位,如果将条件一般化,设计如下变式,有助于提高学生思维的深刻性和灵活性.

变式1 若(1)中∠AOB=α,其他条件不变,求∠MON的度数;

变式2 若(1)中∠BOC= β(β小于90◦),其他条件不变,求∠MON的度数;

变式3 从(1),(2),(3)的结果中能看出什么规律?

2.渗透数学思想方法注意问题

2.1 逐步渗透

由于领悟数学思想方法有一定难度,所以教学中比较流行的做法是将数学思想方法单独安排专题教学,而且只安排在毕业班,以为这样可以速成.《初中数学课程标准》要求“对于重要的数学思想方法应体现螺旋上升的、不断深化的过程,不宜集中体现”,所以从七年级数学教学开始,就要逐步渗透数学思想方法.

2.2 激发兴趣

对于刚刚升入七年级的学生来说,绝对值、角平分线、整式等知识点开始会觉得生涩难懂.为了让学生体会思想方法对解题带来的好处,课上教师要精心组织,充分发挥学生的主体作用,多创设情景,多提供机会,在学生主动参与的教学活动中感悟思想方法的妙处.教师如果只是通过举例点出思想方法的概念,然后希望学生能主动的用也许是一厢情愿.即使学生知道什么叫思想方法,但是什么时候用,怎么用还需要悟的过程.

2.3 理顺层次

《数学新课标》对初中数学中渗透的数学思想方法划分为三个层次,即“了解”、“理解”和“会应用”.“了解”即对数学思想方法的含义有初步的感性认识,“理解”即能够知道它们有什么用途,“会应用”即在理解的基础上,能用它去解决一些问题.在教学中,要认真把握好“了解”、“理解”、“会应用”这三个层次.不能随意将“了解”的层次提高到“理解”的层次,把“理解”的层次提高到“会应用”的层次.不然的话,学生初次接触就会感到数学思想、方法抽象难懂,高深莫测,从而导致他们失去信心.如“分类”思想在初中的要求是“了解”,在高中的要求才是“理解和应用”.我们在教学中,应牢牢地把握住这个“度”,千万不能随意拔高、加深,否则,教学效果将得不偿失.

后记 数学思想方法,源于知识又高于知识.在渗透过程中,一方面要根据七年级学生实际不要操之过急,另一方面应把握时机,让学生主动参与,接受熏陶,不断提炼思想方法、形成用思想方法指导思维活动,培养学生终身学习和发展的意识和能力.