深度学习概念指导下“递进型”变式教学的实践—以高三函数零点问题复习课为例

北京市通州区潞河中学(101149) 赵月灵

信息时代的到来,逼迫着教学必须从农耕时代的朴素的“教学即传递”的观念中走出来,也从非此即彼的各种形式化的改革中走出来,重新认识教学的任务与功能.教学为了发展,教学要促进发展,教学要让学生具备自主发展的意识与能力,要发展学生的核心素养.这,成为当前紧迫的任务,深度学习的研究成为信息时代背景下的新任务.

因此我们首先要弄清楚两个概念,即何谓深度学习?何谓变式教学?

所谓深度学习,就是指在教师引领下,学生围绕着具有挑战性的学习主题,全身心积极参与、体验成功、获得发展的有意义的学习过程.在这个过程中,学生掌握学科的核心知识,理解学习的过程,把握学科的本质及思想方法,形成积极的内在学习动机、高级的社会性情感、积极的态度、正确的价值观,成为既具独立性、批判性、创造性又有合作精神、基础扎实的优秀的学习者,成为未来社会历史实践的主人.

所谓“变式教学”,就是围绕一个问题本质,在基本思路不变的基础下,不断变更问题的情境,使事物的一些外在属性不断迁移、变化,从而使学生不断调整思维、思考的角度,把问题转化成原问题本质的一种教与学的方法.是践性叶澜教授:“把课堂还给学生,让课堂充满生命活力”的有效途径.开放性“变式教学”是学生主动建构的课堂,是学生做学习的主人的课堂.笔者近几年来坚持通过“变式”的数学教学活动,培养和提高学生的数学转化能力,收到较好的效果.

下面就高三教学中“函数零点问题”的复习教学谈谈自己在这方面的实践.

一、由常数到参数,揭示问题解决的基本方法,培养学生思维的深度.

例题1 已知函数发f(x)=lnx+1求函数y=f(x)的零点.

变1 已知函数f(x)=lnx-x+1求函数y=f(x)的零点的个数.

变2 已知函数f(x)=lnx-ax+1,a∈R常数,讨论函数y=f(x)零点的个数.

方法1 转化为函数f(x)=lnx-ax+1在(0,+∞)上与x轴交点的情况.

这种方法的难点是函数里含有参量a,所以要对a进行讨论,分类较多,往往会使问题复杂化.

评析 由于分离了参量,回避了分类讨论,思路变得简洁清晰.

方法3 由f(x)=0⇒lnx-ax+1=0(x＞0),即lnx=ax-1.转化为求函数y=lnx与直线y=ax-1交点的情况.由于函数y=lnx和一次函数y=ax-1均为基础函数,且y=ax-1的图象必过(0,-1)点,所以数形结合也很容易得到结果.

解题回顾 例题1主要是让学生明白函数零点的概念和最根本的解法;变式1当零点直接不好求时,通过转化为两个函数图像交点求零点个数;变式2加入参数,变为零点的逆向问题,本题所展示的三种解题方法同时也是解函数零点的问题的三种主要方法(直接法、分离法、转化为两个基础函数图像交点法).这个环节的变式,引导学生学会紧紧抓住函数零点概念,适当进行函数零点、相应方程的根、函数图像与轴的交点、两个函数图像的交点的相互转化.

“解题”是数学学习,特别是高考复习的主要活动.设计好变式将问题隐藏在题目之中,让学生在教师的追问、反问、补问把掩藏在解法背后的想法挖掘出来.让学生做到知其然更要知其所以然.在深度学习中,学生是学习的主体,教师是引导者而非学生学习的替代者,教学内容不是只需学生记忆的、外在于学生的静态的、客观知识,而是需要学生全身心投入去理解、领会、评判、体验、感受才能“活”起来、“动”起来的知识.

二、改变不同问法,揭示问题,培养学生思维的广度.

到这个程度学生对函数零点问题真的理解掌握了吗?如果学生没有很好重视解后的反思、再变化和引申等重要环节,题目稍作变化可能就不会解决了.

所以需要再设计了一系列的对比问题:

变3已知函数f(x)=lnx-ax+1,a∈R常数,

(1)若y=f(x)在区间(1,e)上恰有两个零点,求a的取值范围;

(2)若y=f(x)与x轴有且只有一个公共点,求a的取值范围;

(3)方程lnx-ax+1=0有两个根求a的取值范围;

至此学生明白了函数零点问题、方程根的问题、两个函数图像交点问题可以相互转化,都可以用解决零点的三种主要方法解决.学生也在总结中用了“一箭多雕”这个词,即掌握了“函数零点”问题的解决办法,方程根的问题和函数图像交点的问题也都一样解决了.紧接着给出下题;

例2 已知函数f(x)=x3-3ax+2a,(a,b∈R),若y=f(x)与x轴有且只有一个公共点,求a的取值范围.

方法1直接分析函数和轴的交点情况,f′(x)=3x2-3a,然后对参量进行讨论,画函数的图像分析;

方法2 x3-3ax+2a=0⇒a(3x-2)=x3.

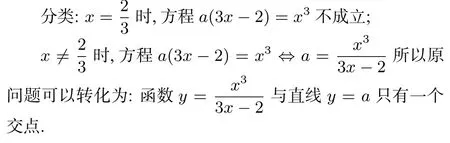
解题回顾 变式3使学生更明确函数零点、相应方程的根、函数图像与轴的交点、两个函数图像的交点等的相互转化;例2检验学生理解的情况,直接应用,但指出了一个易错问题,即分离参量时需要对自变量的取值范围进行讨论.对学生分析如何分离变量、分离时需要注意什么问题,什么时候可以分离,什么时候不能分离给于启发.

在深度学习中,教师的是设计引导者,引导学生不仅能够掌握知识的(文字)符号表达以及(文字)符号表述的逻辑,还能够理解文字符号所传达的意义内容,即对能够教学内容进行深度加工.

因此在解题过程中,不仅要引导学生“求变”,还应“求联”,即在解后反思前后联系,以上这样变换问题的条件和形式,即在原题的基础上创设新的情境,以变式的理念研究解题的方向和优化解题策略,能不断鼓励学生独立思考,深入思考,可使学生思维开阔性得到训练和提高.

三、转换角度,培养学生思维的发散度.

在基本方法和联系的前提下,如果没有灵活性还是不能解决,

交点的情况.

······

分析发现方向1比较简单易行,所以采用方向1来解决.

通过把两个函数图像交点,转化为相应方程的根,适当变形,再把方程的根转化为两个函数图像的交点,确定方向,问题很容易得到解决.

解题回顾 例题3涉及到如何运用已有的知识储备,灵活分析转化的问题,让学生明白为什么转化的多方向,然后通过优化确定合适的方向.任何东西都不是死东西,我们要引导学生变换思维的角度,运用转化的思想,化归的方法,把要解决的问题化归为已经解决或比较容易解决的问题.这样对数学的认识也就表现为一种多角度、全方位的上升过程.学生的思维的创造性和灵活性得到有效的训练和提高.根的情况→函数y=x和

四、创设新的情境,引导灵活转化,培养学生思维的创造性和灵活性.

例题4 已知函数f(x)=2x3-3x.若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围;(本题是2014年北京文科20题第二问)

变式 已知函数f(x)=(4-x)ex-2(x＜2),若存在直线ax-2y+m=0(a、m为常数)与曲线y=f(x)相切,求a的范围.

分析 f′(x)=(3-x)ex-2(x＜2)由ax-2y+m=0所以原问题可转化为(3-x)e在x∈(-∞,2)有解,即函数g(x)=(3-x)x∈(-∞,2)存在零点的问题.

解题回顾 例题4和这两个问题表面是切线的问题,但通过分析只需转化为零点问题就可以了,自然得到解决.

教师设计问题的有效性,直接决定学生思考的深度,设计新的问题背景,对问题进行迁移和拓展变化.然后引导学生大胆转化,找到方法和规律,学会对问题反思,增强解决问题的灵活性.

五、延伸新的外围,拓宽思维链,培养学生思维的广泛性.

课堂教学的时间毕竟是有限的,如何才能提高课堂的效率,增加学生学习的深度和广度,加强有效性,为此,笔者合理利用原有教学资源,在原有情景中“求变”,帮助学生拓展到课堂教学的外围,延伸课堂教学的信息容量.

首先,为了使学生在课堂学习的基础上,对知识有更加深刻的认识和理解,从中总结提炼出各自学习和发展所掌握的东西,在课堂上的反思交流总结.

比如:让学生的交流、反思、总结、提取零点问题知识结构.理清函数零点问题、方程根的问题、函数图像交点问题间的转化关系,

零点问题主要有三条路,方法①直接求函数图像和x轴的交点,这种方法由于要对参量进行分类讨论,所以一般较为麻烦;方法②是转化为相应的方程,然后把参量分离出来,通过图像来看函数图像与一条平行于轴直线交点的个数比较简单,局限性是有时不能分离参量.方法③是函数零点转化为方程的根,然后适当分配,转化为看、两个简单函数图像的交点.

体会了数学题目的发展变化及解法的发现过程,引导尝试自己去发现、再创造,再探索.采用小组互助学习的方式去探究问题.

延伸题目 设函数f(x)=lnx,g(x)=ax-1,a∈R,f(x)＞g(x)恒成立.求a的范围?

让学生自己学着用方程解决问题的方法去解决不等式的问题.为了使学生进一步自我体验数学发现和创造的历程,学会自主探究与合作交流相结合的学习方式.

新课程倡导积极主动《标准》明确提出数学教学必须鼓励学生积极参与数学活动,不仅是行为上的参与,更要有思维上的参与,通过各种方式激活思维,深化思维,不断地提高数学思维能力.在高中数学教学中采用递进型变式教学,从典型的例题出发引导学生去变化、去引申、去发现,变中求活,变中求新,这样就能逐步提高学生发现问题、分析问题和解决问题的能力,同时也能不断提高学生的思维品质和数学素养.