分析层合材料槽孔应力的新型特殊层合杂交应力元
杨庆平,王安平,田宗漱
(1.南京理工大学 能源与动力工程学院,南京 210094;2.中国科学院空间应用工程与技术中心,北京 100094;3.中国科学院大学,北京 100080)
0 引 言
工程结构中大量遇到具有槽孔的层合材料构件,由于槽孔的存在,可能在孔边横截面上产生高的局部应力,导致构件分层破坏。因此,研究槽孔附近应力的正确分布,对分析构件的破坏机理及确保其安全,具有重要意义。
对于槽孔边沿的影响问题,正如Wang及Choi[1-2]所指出的,由于它们存在以下内在的复杂性:各层力学性质强烈的各向异性;通过板厚度方向材料的突然改变;沿板边界几何形状的不连续性;靠近层合材料边沿区域平面和横向变形与应力的耦合;准确满足自由边无外力条件的困难等原因,致使这类问题的研究一直进展缓慢。
鉴于有限元方法的通用性及简易性,对于具有一个中心圆孔层板承受拉伸时的应力,许多学者应用不同类型的有限元进行过分析:Chauduri等[3-4]应用新型三维板壳理论及势能原理建立的三角形元;Temiz等[5]依据等参位移元;Hu等[6-7]采用三维等参元;Pian及Li[8]利用杂交应力层合元;Nishioka等[9]依据一种特殊元;李及谢[10]则采用了一种拟三维有限元迭代法;Tian、Spilker等[11-14]利用基于一种修正余能原理的特殊元。
数值结果表明,层合材料靠近边沿很小局部区域内,呈现一种应力梯度快速变化的复杂三维应力状态。由于有限元的收敛速度由邻近高应力梯度区域解的性质所支配,用一般假定位移元及一般假定应力元求解不仅精度不理想,而且收敛很慢,也就是根据高阶多项式插值函数所构造的一般高精度元,对改善这种工况下的收敛速度无益,除非应用极密的计算网格,否则难以得到精确的自由孔边应力分布[15-18]。
本文依据田所导出的一种非匀质材料的扩展Hellinger-Reissner原理[19],建立了一种新型具有一个无外力圆柱表面的三维杂交应力元。对于具有圆柱形槽孔的层合构件,它提供较一般假定位移元及一般杂交应力元准确的孔边三维应力分布。此种元亦可有效地分析具有倒圆角矩形孔、U-型孔、拟椭圆孔的多类圆柱型槽孔的层合板自由孔边的三维应力分布。
1 非匀质材料的扩展Hellinger-Reissner原理[19]
当物体被离散为n个有限元时,其扩展的Hellinger-Reissner原理为
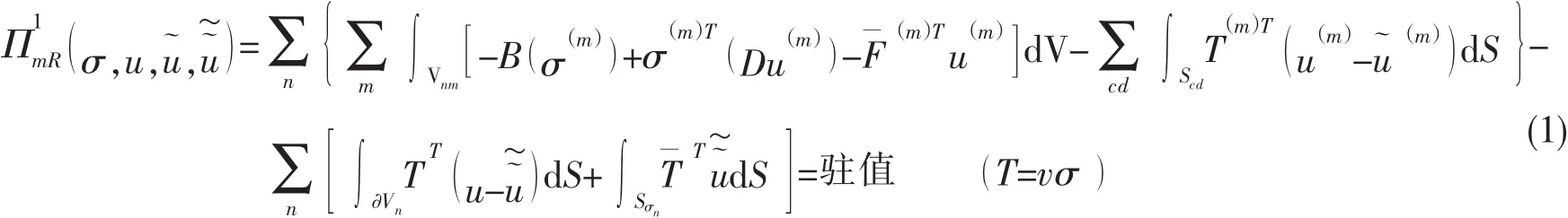
约束条件
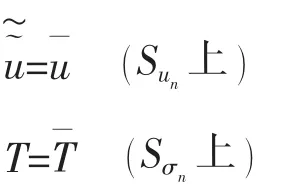
式中:B(σ )为材料余能密度;σ 为应力;D为微分算子阵;u为位移;及分别为已知的体积力、位移及表面力;Vnm为第 n 个元内第 m 个子域的体积;∂Vn为第 n 个元的外表面,∂Vn=Sσn∪Sun∪Sab;Sun为第 n个元的位移边界;Sσn为第n个元外力边界;v为边界外向法线方向余弦;m为子域数;)及)分别为第n个元内第m个子域的应力、位移及已知体积力;u~为子域c与d间引入的子域间位移;u~~为单元a与b间引入的元间位移;Sab及Scd为元a、b间及子域c、d间的边界面。
当在上式的层间及元间再引入条件
层间
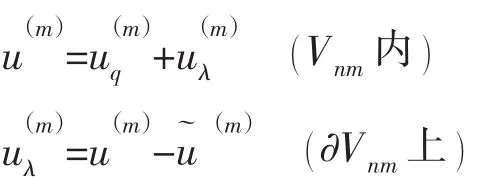
元间
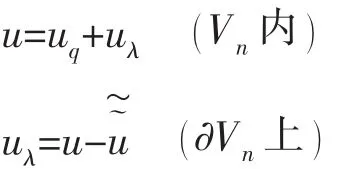
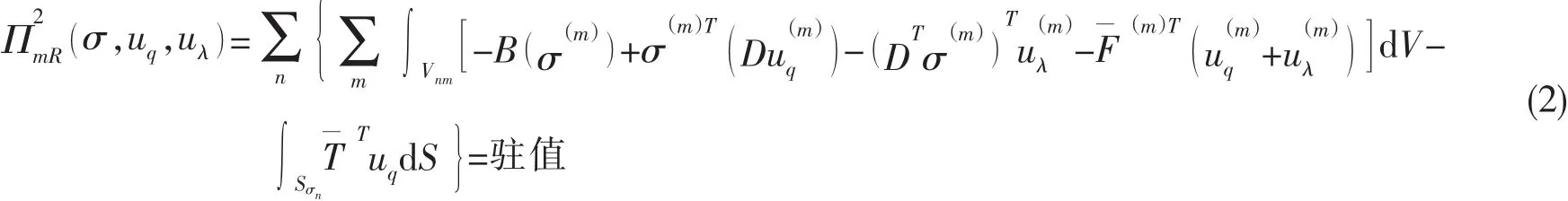
约束条件
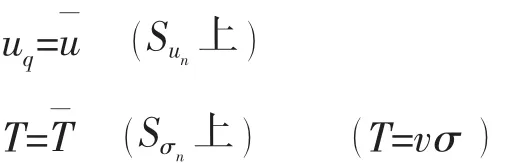
2 层合元列式[19]
推导单元刚度矩阵时可以只考虑一个元,不计体积力及表面力。对线弹性体,(2)式给出的能量表达式为
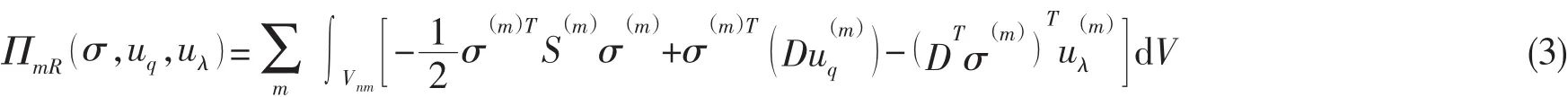
对各层选取

根据Pian等所提出的杂交应力元理性列式方法[20],利用下式

作为应力约束条件。同时,为了避免应力场中的高阶项与常数项发生耦合时,单元不能通过分片试验,根据田等建议[23],将应力)分为高阶项)及常数项)两部分,将平衡约束条件(5)也改为以下两部分:

这样,能量泛函(3)成为
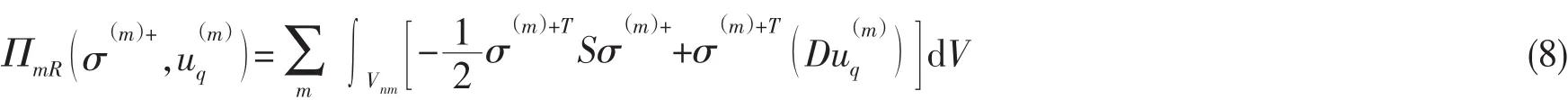
同时,由于(4)式可知

代入(8)式,得
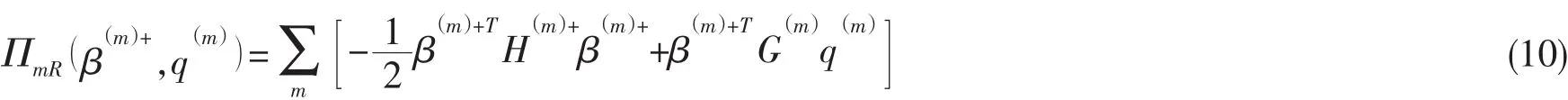
式中


再代入(10)式,即得到单元刚度阵

3 具有一个无外力圆柱表面的三维杂交应力层合元
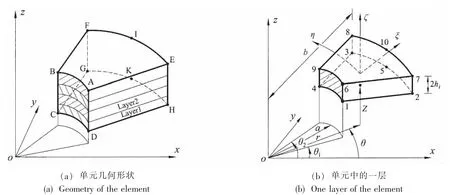
图1 具有一个无外力圆柱表面的三维杂交应力层合元Fig.1 Geometry of the three-dimensional multilayer hybrid stress element with a traction-free cylindrical surface
具有一个无外力圆柱表面的新型三维应力杂交层合元,单元形状如图1所示。无外力表面,指单元外表面上无任何外载荷作用的自由表面,这里为图中阴影部分的圆柱面ABCD。本特殊元严格满足此圆柱表面上无外力作用的边界条件。面ABCD和EIFGKH是两个圆柱面,面ADHE和BCGF沿径向并相交于z轴上。单元的下表面CDHKG和上表面BAEIF平行,并与z轴垂直。
3.1 单元位移场
由于可能发生弯曲/拉伸耦合现象,而且厚的层板也会产生严重的横截面翘曲。而前述变分原理的有限元列式可用于对每层横向剪应变均独立处置的厚层板,因此单元位移场选择每层横截面可以独立的转动。
(1)单元协调位移uq
选取协调位移uq为
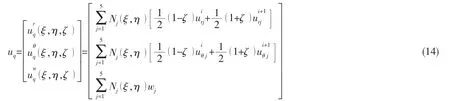
j
单元的结点位移
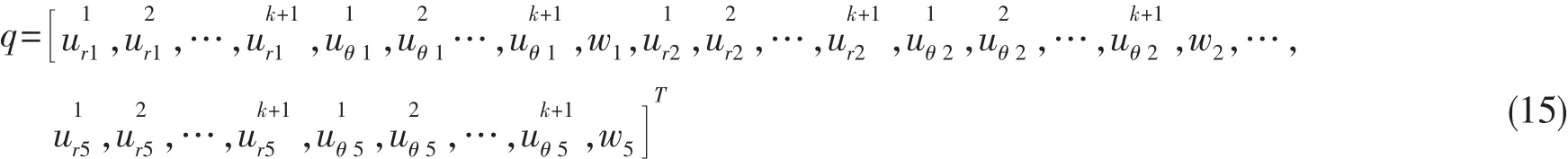
式中:k为总层数。
(2)单元内位移 uλ
展开协调位移场 uq,知其为 ξ,η,ζ的非完整二次多项式,缺 ξ2和 ζ2两项;三次项缺 ξ2η,ξ2ζ,ξζ2,ηζ2,ξ3,η3,ζ3七项。 通过选取元内位移 uλ补足所缺的项,得到
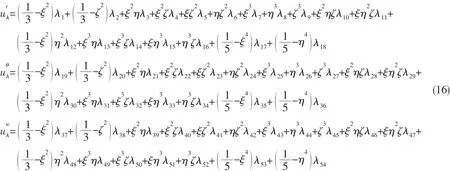
3.2 单元假设应力场
初始应力场选取为自然坐标表示的非耦合完整的二次式。
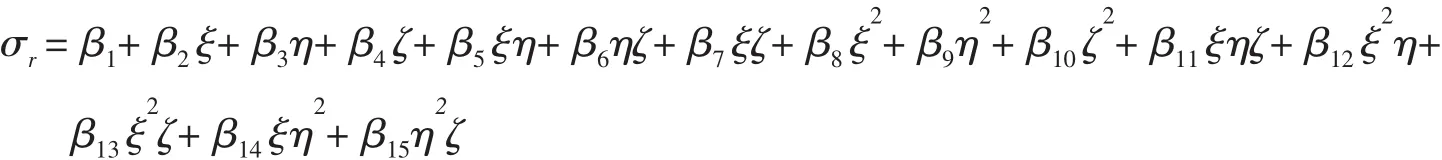
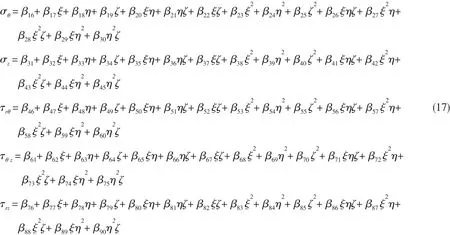
利用理性约束平衡方程式(6)及(7),可消去35个β。
圆柱面无外力边界条件

及层间应力互等和底面无外力条件

(19a)式,表示单元下一层上表面的层间应力与上一层下表面的层间应力相等,满足了此条件,在单元的层间界面上,应力 σz,τrz,τθz保持连续。 (19b)式,表示单元的底面上无外力作用。 (19b)式不是扩展变分原理(2)的必要条件,加入此条件,也不影响此原理的应用。如元的底面上有外力作用,则代入相应条件即可,无妨以下推导。
另外,单元引入了元内位移uλ,因此在层间界面上位移u,v,w是不连续的。
利用(18)式、(19a)式及(19b)式,再消去40个β。这样,总共消去 75个β。最终得到第i层的应力场
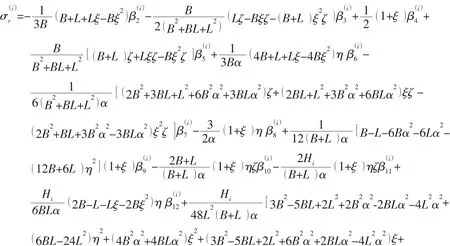

式中
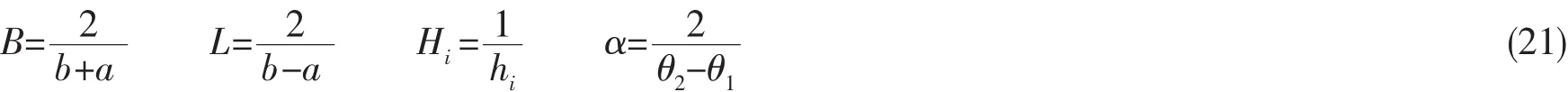
这个应力场(20)及位移场(14)和(16)组成单元 Case A。
4 算 例
4.1 中心拟椭圆孔层板承受拉伸
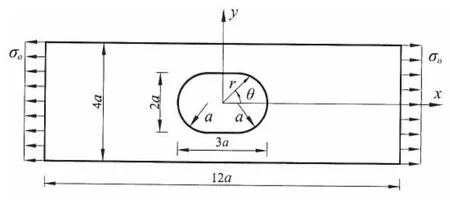
图2 中心拟椭圆孔层板承受拉伸Fig.2 Laminate plate with a quasi-elliptic hole under tension
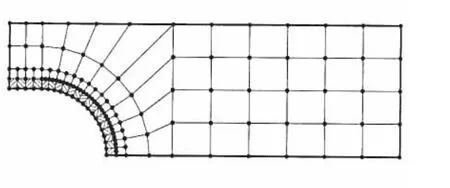
图3 1/8构件有限元网格Fig.3 The mesh of 1/8 of structure

表1 层合板单层材料特性Tab.1 Material properties of a single laminar
两端承受拉伸,中心拟椭圆孔[±45 ]s层板如图2所示,每层厚度h=0.2a,材料特性见表1。取1/8板进行有限元分析,有限元网格见图3。
沿孔边圆柱表面(图中影线部分)用本文建立的特殊元;孔直边表面用田、赵等[17]建立的具有一个无外力直表面的杂交应力层合元,其余部分用Pian等建立的一般三维杂交应力层合元[24]和10结点三维等参位移层合元联合求解。
此问题没有解析解,用8结点一般三维位移层合元(ANSYS中“Solid46”单元),及三级子结构所得结果作为参考解,其各级结构的自由度分别为393、800和2 002,总自由度 3 195(图 4)。
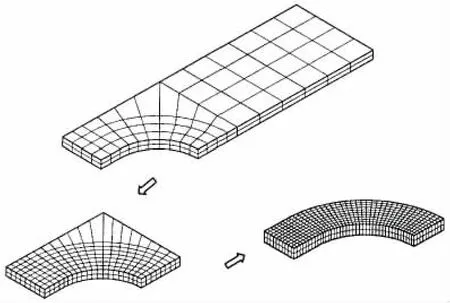
图4三级子结构技术Fig.4 Sub-structuring technique
θσ0值,图6-7分别给出应力σr及τrθ沿径向的分布。可见,现在特殊元得到的解相当接近参考解。计算得最大环向应力为 σθ/σ0=6.106(θ=32.27°,[±45]s,z=h);相应参考解为 6.622(θ=32.40°),误差为-7.8%。
而现在特殊元Case A求解所用自由度为1 000,仅为一般三维等参位移层合元方法的1/3。
表2 计算的层板孔边环向应力Tab.2 Computed circumferential stress

表2 计算的层板孔边环向应力Tab.2 Computed circumferential stress
单元类型 自由度数[+4 5/-4]5 s,z=h [9 0/]0 s,z=2 h σ θ max/σ 0 误差(%) θ σ θmax/σ 0 误差(%) θ 1 2 C a s e A参考解1 0 0 0 3 1 9 5 6.1 0 6 6.6 2 2-7.8 3 2.2 7°3 2.4 0°8.1 9 0 7.8 8 1 3.9 6 3.4 4°6 3.4 4°
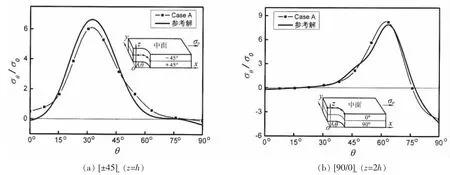
图5 孔边环向应力σθ分布Fig.5 σθdistribution along the rim of the hole
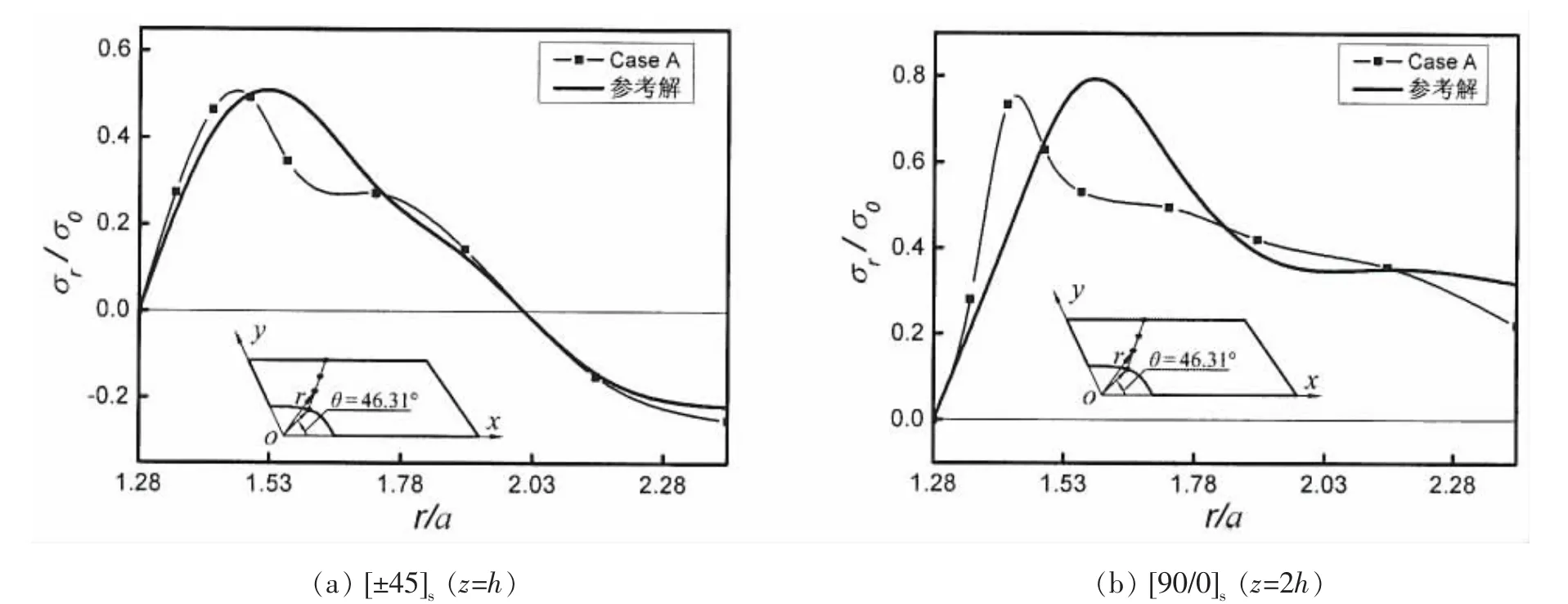
图 6 应力σr沿径向分布(θ=46.31°)Fig.6 σrdistribution along the radial direction(θ=46.31°)
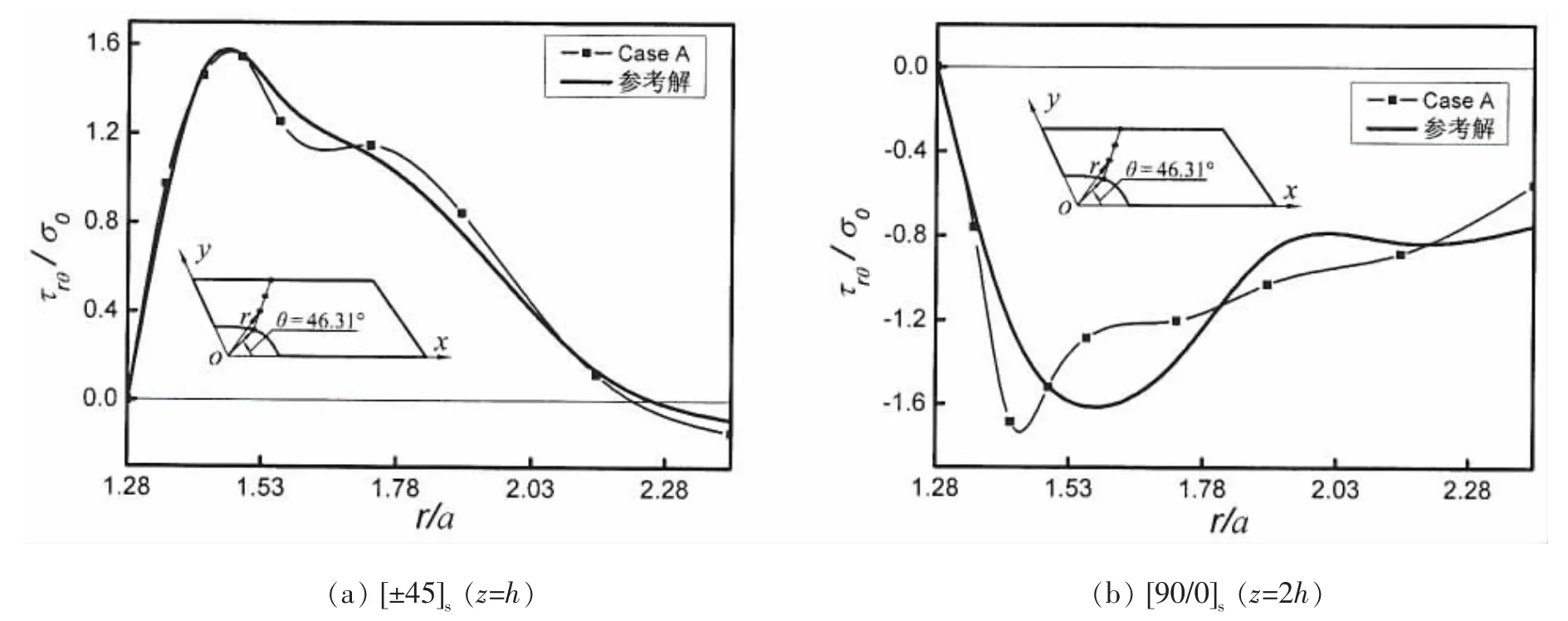
图 7 剪应力 τrθ沿径向分布(θ=46.31°)Fig.7 τrθ distribution along the radial direction(θ=46.31°)
4.2 单侧U型槽层板承受拉伸
考虑图8所示单侧U-型槽层板,各层厚0.2a,材料特性见表1。图9给出1/4板有限元网格,图中沿孔圆柱表面用本文建立的特殊元,孔直边表面用田、赵等建立的元[17],其余部分用Pian等建立的一般杂交元[24]和10结点等参元。计算所得孔边正则化环向应力σθ分布由图10给出,图11则给出沿径向剪应力 τrθ的分布。 同样可见,对于 σθ及 τrθ,Case A的解也很接近参考解。 对于[90/0]s板为19.22,相应参考解20.35,误差为-5.6%。参考解同样用子结构法求得,所用自由度分别为840、1 950和5 162,总的自由度为7 952,而现在特殊元求解所用自由度为758(图9),仅为位移层合元的1/10。
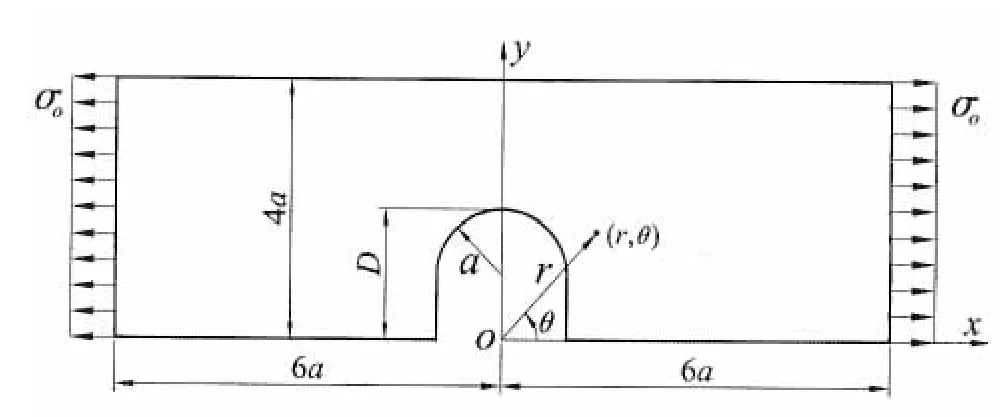
图8 单侧U型槽层板承受拉伸Fig.8 Laminate plate with a U-shaped groove under tension
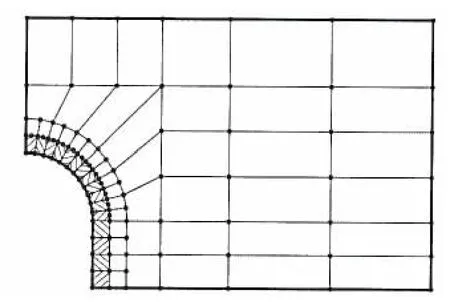
图9 1/4板的有限元网格Fig.9 The mesh of 1/4 of structure
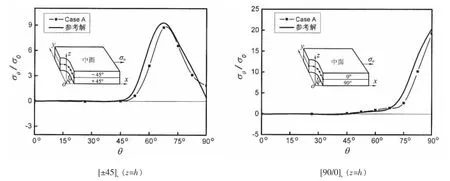
图10 孔边环向应力σθ分布Fig.10 σθdistribution along the rim of the hole
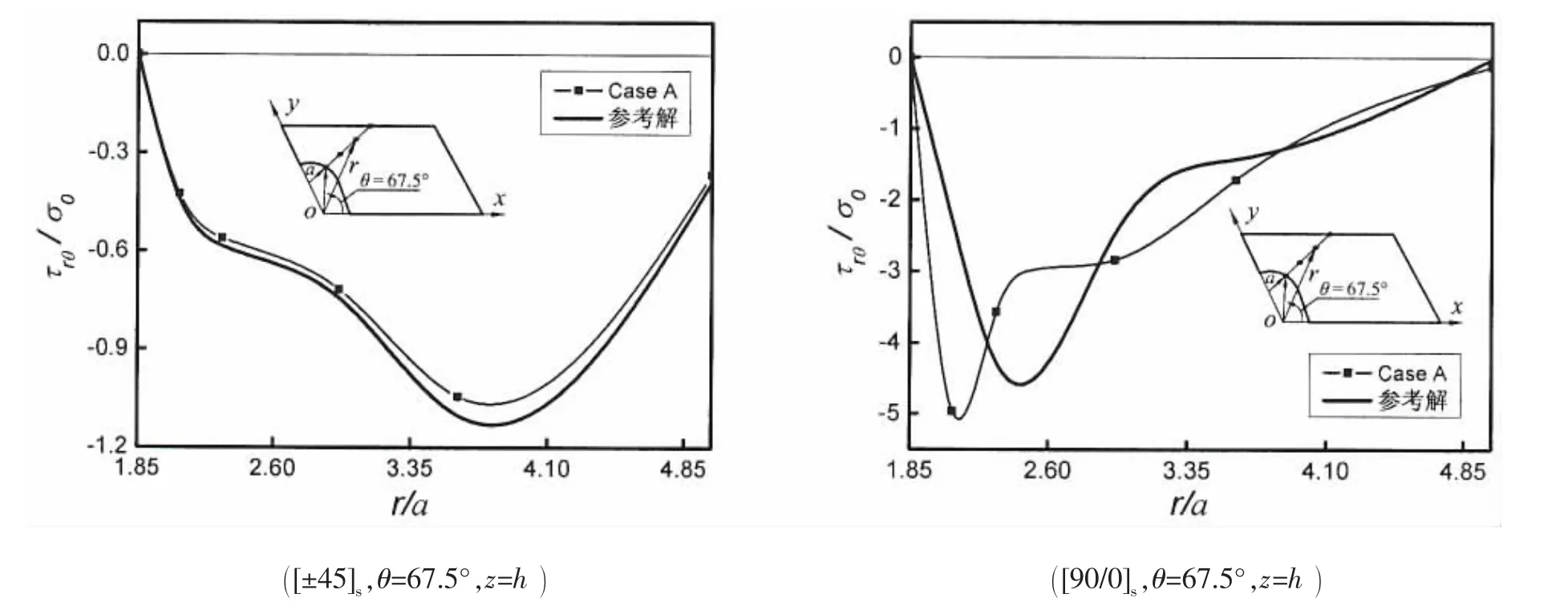
图 11 剪应力 τrθ沿径向分布(θ=67.5°)Fig.11 τrθ distribution along the radial direction(θ=67.5°)
5 结 论
本文利用一种非匀质材料扩展的Hellinger-Reissner原理,及依据此原理当应力及位移分布不连续的非匀质有限元刚度列式,建立了具有一个给定无外力圆柱表面的层合杂交应力元。
单元应力场将Pian等发展起来的匀质各向同性材料的杂交应力理性列式扩展至层合材料。它保存了此理性列式两大基本点:(1)引入非协调位移,使所选应力与位移相匹配,以提高单元求解精度;(2)引入自然坐标进行应力及位移插值,从而明显地降低了单元形状歪斜对其精度的敏感性。
数值算例表明,在十分粗的网格下,此新的层合元不仅可提供较一般假定位移元及一般假定应力元准确的孔边应力,而且也可用于具有穿透圆孔、或半穿透圆孔层合构件柱形自由边的应力分析。
[1]Wang S S,Choi I.Boundary-layer effects in composite laminates:Part 1:free-edge stress solutions and basic characteristics[J].Journal of Applied Mechanics-Transactions of the ASME,1982,49:541-548.
[2]Wang S S,Choi I.Boundary-layer effects in composite laminates:Part 2:free-edge stress solutions and basic characteristics[J].Journal Applied Mechanics-Transactions of the ASME,1982,49:549-560.
[3]Chauduri R A.A new three-dimensional shell theory in general(non-lines-of-curvature)coordinates for analysis of curved panels weakened by through/part-through holes[J].Composite Structures,2009,89:321-322.
[4]Wu Z,Chen W J.Stress analysis of laminated composite plates with a circular hole according to a single-layer higherorder model[J].Composite Structures,2009,90:122-129.
[5]Temiz S,Özel A,Aydinfe M D.FE stress analysis of thick composite laminates with a hole in bending[J].Applied Composite Materials,2003,10:103-117.
[6]Hu E Z,Soutis C,Edge E C.Interlaminar stresses in composite laminates with a circular hole[J].Composite Structures,1997,37:223-232.
[7]Yang Z,Kim C B,Cho C D,Beom H G.The concentration of stress and strain in finite thickness elastic plate containing a circular hole[J].International Journal of Solids and Structures,2008,45:713-731.
[8]Pian T H H,Li M.Stress analysis of laminated composites by hybrid finite elements[C]//Kuhn G,Mang H.Discretization Methods in Structural Mechanics,IUTAM/IACM Sym.Vienna,1989:539-548.
[9]Nishioka T,Atluri S N.Stress analysis of holes in angle-ply laminates:an efficient assumed stress‘special-hole-element’approach and a simple estimation method[J].Computers and Structures,1982,15:135-147.
[10]Li R F,Xie Z C.New finite element method for interlaminar stress analysis of composite laminates at free edge[C]//Cheung Y K,et al.Computational Mechanics,Proceeding of the Asian Pacific Conference Computational Mechanics Part 2(of 2).Rotterdam:Balkema A A,1991:1025-1030.
[11]Tian Z S,Liu J S,Ye L,Pian T H H.Studies of stress concentration by using special hybrid stress elements[J].International Journal for Numerical Methods in Engineering,1997,40:1399-1412.
[12]Tian Z S,Tian Z.Improved hybrid solid elements with a traction-free cylindrical surface[J].International Journal for Numerical Methods in Engineering,1990,29:801-809.
[13]Tian Z S,Zhao F D and Tian Z.Special hybrid stress element for stress analyses around circular cutouts in laminated composites[J].Science in China(Series E),2001,44(5):531-541.
[14]Spilker R L,Chou S C.Evalution of hybrid-stress formulation for thick multiplayer laminates[C]//Lenoe E M,Oplinger D W,Burke J J.Proceeding of 4th Conference on Fibrous Composites in Structural Design.New York:Plenum Press,1980:399-410.
[15]Spilker R L,Chou S C.Edge effects in symmetric composite laminates:importance of satisfying the traction-free-edge condition[J].Journal of Composite Materials,1980,14:2-20.
[16]Lakshminarayana H V.Stress distribution around a semi-circular edge-notch in a finite size laminated composite plate under uniaxial tension[J].Journal of Composite Materials,1983,17:357-3610.
[17]Tian Z S,Zhao F D,Yang Q P.Straight free-edge effects in laminated composites[J].Finite Elements in Analysis and Design,2004,41:1-14.
[18]Tian Z S.A study of stress concentration in solids with circular holes by 3-dimensional special hybrid stress finite elements[J].Journal of Strain Analysis,1990,25:29-35.
[19]田宗漱,卞学鐄.多变量变分原理与多变量有限元方法[M].北京:科学出版社,2011.Tian Z S,Pian T H H.Variational principles in multiple variables and finite element mothods in multiple variables[M].Beijing:Sciences Press,2011.
[20]Pian T H H,Sumihara K.Rational approach for assumed stress finite element[J].International Journal for Numerical Meth-ods in Engineering,1984,20:1685-1695.
[21]Pian T H H.Finite elements based on consistently assumed stresses and displacements[J].Finite Elements in Analysis and Design,1985,1:131-140.
[22]Pian T H H,Tong P.Relations between incompatible displacement model and hybrid stress model[J].International Journal for Numerical Methods in Engineering,1986,22:173-181.
[23]Tian Z S,Tian Z S.Further study of construction of axisymmetric finite element by hybrid stress method[C]//Proceeding of Third International Conference on Education,Practice and Promotion of Computational Methods in Engineering Using Small Computers.Macao,1990:549-558.
[24]Pian T H H,Mau S T.Some recent studies in assumed stress hybrid models[C]//Oden J T,Clough R W,Yamanoto Y.Advances in Computational Methods in Structural Mechanics and Design.Alabama:University of Alabama in Huntsville Press,1972:87-106.

