模型试验验证WAVEWATCH-III波浪演化

邹 丽 ， 孙 泽 ， 宗 智 ， 王 振 ， 蔡志文 ， 刘小龙

（1.大连理工大学 船舶工程学院，辽宁 大连116024；2.中国船舶科学研究中心，江苏 无锡214082；3.工业装备结构分析国家重点实验室，辽宁 大连 116024；4.大连理工大学 数学科学学院，辽宁 大连116024）

0 引 言

波浪在复杂海洋地形中传播时，需要经过多变的海底和复杂岛礁地形；而岛礁附近一般有几公里的珊瑚礁浅滩，这导致流和波浪在岛礁附近的绕流和传播极其复杂，存在过顶绕流和三维绕流现象，伴随有爬坡、折射，绕射、波浪破碎等非线性复杂问题。对海洋岛礁近岸水波的数学建模应该能够准确地描述水波运动的主要特征（波形的传播，色散，波的折射、反射和绕射，波能的传播，浅水效应，波的衰减，扩散，破碎、爬坡等）。

基于能量平衡的波浪计算模型，或称为波能谱或波作用密度谱模型。该模型基于波浪传播过程中波谱作用量平衡原理，建立求解方程。它主要用于深海波浪的计算，亦适用于近海大范围的波浪计算。本文针对岛礁周边远场较深水深的波浪传播，采用动谱平衡方程模型中的WAVEWATCH-III模型处理。WAVEWATCH-III是在NOAA/NCEP发展的第三代波浪模型，也是基于NASA戈达德宇宙飞行中心研发出的WAVEWATCH-II，代尔夫特理工大学研发的WAVEWATCH-I模型发展而来的。WAVEWATCH-III不仅仅是一个波浪模型，它更像是一个处理波浪相关问题的平台，科研工作者允许自行开发解决波浪问题的物理和数值方法。许多学者利用风场资料驱动，在WAVEWATCH-III模型下对各大海域进行的数值模拟预报，取得了符合实测资料的结果。Feng和Vandemark等（2004）[1]将该模型应用于修正卫星测量的海平面高度，分析对比了纯NCEP风场和NCEP/QSCAT混合风场驱动下模型计算所得的波浪场，包括了全球范围和局部海洋范围内的情况。Browne等（2006）[2]用WAVEWATCH-III结合人工神经网络的经验方法估算了近岸的波浪，认为这种方法比直接应用近岸模型SWAN的效率更高。齐义泉等（2003）[3]用WAVEWATCH-III模拟了1996年南海海浪场，并对结果进行了分析，他们采用的驱动风场是NCEP风场。李明悝等（2005）[4]用QSCAT/NCEP混合风场模拟了东中国海风浪场，参照日本气象厅发布的浮筒数据，证实风场和计算所得有效波高与实测值符合得很好。

本文利用WAVEWATCH-III对具有复杂地形的近岸海域波浪演化进行数值模拟。忽略风场影响，采用江苏科技大学所做的模型试验的地形与工况，与模型试验结果进行分析对比，分析了误差来源，验证了WAVEWATCH-III对近岸波浪场模拟的有效性，为应用此模式进行更深一步的波浪数值模拟提供了参考依据。

1 控制方程

对于随机海浪来说，海面的不规则变化可以用谱密度E描述，这种海浪谱通常称作能量谱，可以表示为相参数的函数再考虑时间和空间的变化，就可以写成其中为波数矢量，σ，ω分别为固有频率和绝对频率，分别代表地理空间和时间。参数，σ，ω不是相互独立的，它们通过波动的频散关系和多普勒方程建立联系。WAVEWATCH-III模式选择以波数矢量和方向θ为基本的参数组成谱但模式的输出仍然采用以往模式的频率和方向谱作为基本输出，这两种谱的转换可以通过雅可比向前变换来实现。

假设水深和海流发生显著变化的空间比波幅大，或者说，水深和海流的变化相对波浪来说是缓变，则准非线性波浪理论成立，并存在下面的色散关系和多普勒效应关系：

方程（1）-（3）即可解出波浪频率参数随时空的演化。

波谱E是所有独立相位参数的函数，同时随着时间和空间发生变化；波谱也是方向的函数（方向谱），即也简单写成和传统的方向谱表达式一致。

不考虑海流因素时，波包的能量是守恒的。Whitman等（1974）[5]曾提出，在背景流场不均匀时，能量密度E是不守恒的，而波作用量密度N=E/σ是传播守恒的。即

N代表波作用密度谱，S代表能量密度谱E中的所有源函数，在WAVEWATCH-III中，

上式中各源项分别代表：线性输入、风—浪相互作用、耗散、波浪非线性相互作用、海底摩擦作用和碎波效应（本计算不考虑风场）。

在直角坐标系中，平衡方程（4）写成：

其中：矢量Cg是群速度，由标量群速度幅值Cg和方向θ决定，s是方向θ的一个坐标，m是垂直于s方向的一个坐标。在笛卡尔坐标系下（9）式是成立的。方程（7）-（9）中上标一点代表对时间导数，即x˙=算子是二维哈密顿算子。

方程（3）和（6）为主要的控制方程。求解该方程组就可以获得时空中任一点的波谱。

2 计算说明

2.1 地形前处理

地形采用模型试验对应的实际地形。参照江苏科技大学论文《近岛礁生产生活平台及浮式栈桥系统水动力性能模型试验》[6]，模型地形各测点位置说明见图1所示，图中w1～w18为监测点位置。试验缩尺比1：36，量纲化的测点坐标见表1。

将试验地形数据地形数据转换成海底分布，同时将坐标原点转换到海平面的左下角。由于试验给出的地形分布网格间距较大且间距不等，需要进行插值加密，得到了四种精度的插值方法（网格间距为4.5 m）得到的海底3D分布。由于原地形崎岖不平，不同的差分精度得到的地形分布不同，总体上二阶和四阶得到的地形分布更不光滑，而一阶精度较低，因此本文采用三阶精度的插值结果作为地形分布。三阶插值得到的海底3D分布如图2。

图1 w1～w18测点布置位置示意图（单位：m） Fig.1 Arrangement positions of measuring points w1～w18(unit:m)

图2 三阶插值得到的海底3D分布Fig.2 Submarine 3D distribution obtained by different interpolation methods

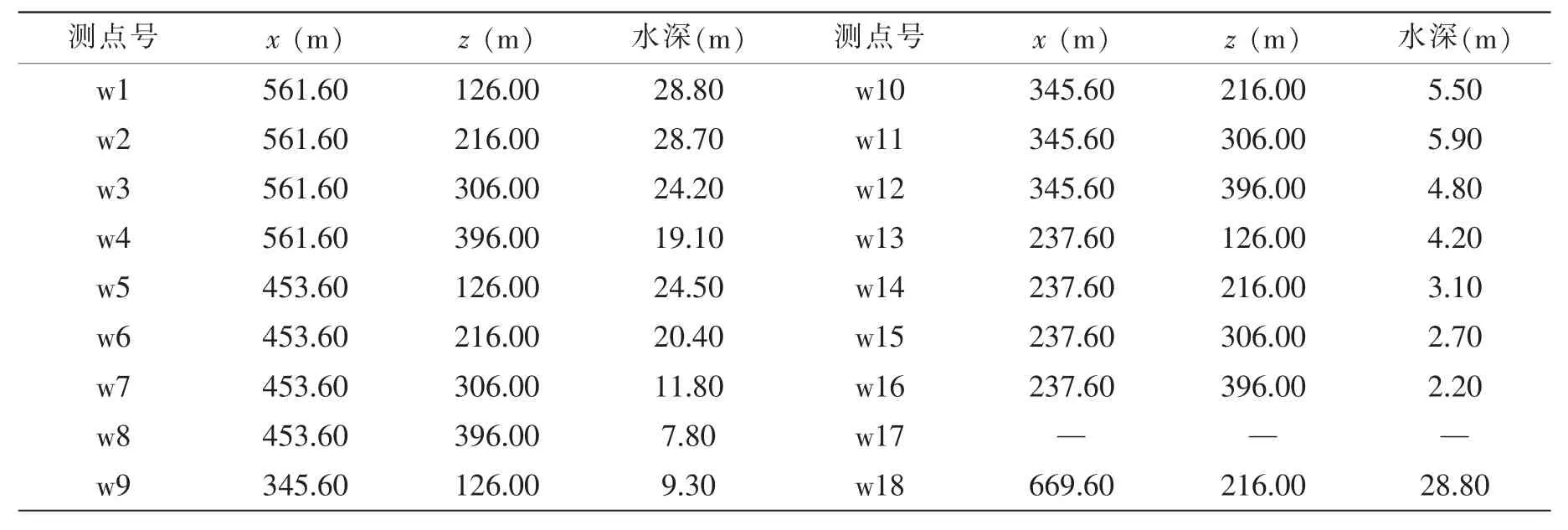
表1 测点坐标位置Tab.1 Arrangement positions of measuring points

2.2 地形网格无关性检验

图3给出了地形网格间距对计算结果的影响。网格间距不同，插值得到的地形分布略有不同。可以看出dx=9 m的结果与dx=4.5 m的结果有一定的差距，而dx=4.5 m的结果与dx=2.25 m的结果接近。根据以往的仿真经验，波频率离散101个点已经足够了，波方向离散72个点也已经足够了。本文计算的网格间距为dx=2.25 m根据以往的仿真经验，波频率离散101个点，波方向离散72个点。

图3 不同网格距离对波高的影响Fig.3 The influence of different grid distance on the wave height

2.3 WAVEWATCH-III模型设置

在模型初始化时，WAVEWATCH-III模式提供了默认设定与用户设定两种开关，表2列出了本文所使用的模型设置参数。

频率分段方法为：

其中分辨率Xσ取1.01，波数的空间分割数m取101。初始频率σ0根据具体工况给出，方向分段数取72。

由于计算工况是不规则波，参照w18位置的试验波浪谱，计算出自定义谱，使得在波浪传播入口w18点的波浪谱与试验波浪谱吻合。

自定义谱的主要输入参数有：波高hs和形状函数其中ql角度逆时针增加，x方向为0，y方向为90，而在WAVEWATCH-III中方向角度x方向为270，y方向为180。根据输入参数，WAVEWATCH-III计算出的能谱分布为：

其中：

表2 模型设置参数Tab.2 Model set parameters

2.4 计算工况

在模型试验中，造波机的位置处于w17，造波机的实际造波能力与设计工况之间有一定误差，所以在WAVEWATCH-III中，计算域入口处w17采用的工况为模型试验中w18处测得的工况经过量纲变换得到。四种工况为不规则波工况，对于不规则波，入口处波谱根据试验波谱插值得到，频率范围选择为0.05到0.25之间，其中横坐标为圆频率（单位为rad/s），纵坐标为能量（单位为cm2s/rad）。具体计算工况参数见表3。

表3 计算工况参数Tab.3 Calculated work condition parameters

3 计算结果分析

3.1 各个计算工况结果与试验对比

本计算对检测点进行了监控，并输出计算定常后的监控点的值，包括有义波高（m）、平均波长（m）、平均周期（s）、平均方向角（°）、方向偏转角（°）等。四种计算工况检测点的信息以及与实验的比较（某些监测点由于缺少试验数据而未给出），其中，波谱波高即为试验测得的的有义波高，波高绝对误差等于波谱波高减去计算波高，波高相对误差等于波高绝对误差与计算波高之比，各个测点的计算结果在下表4-7中给出。

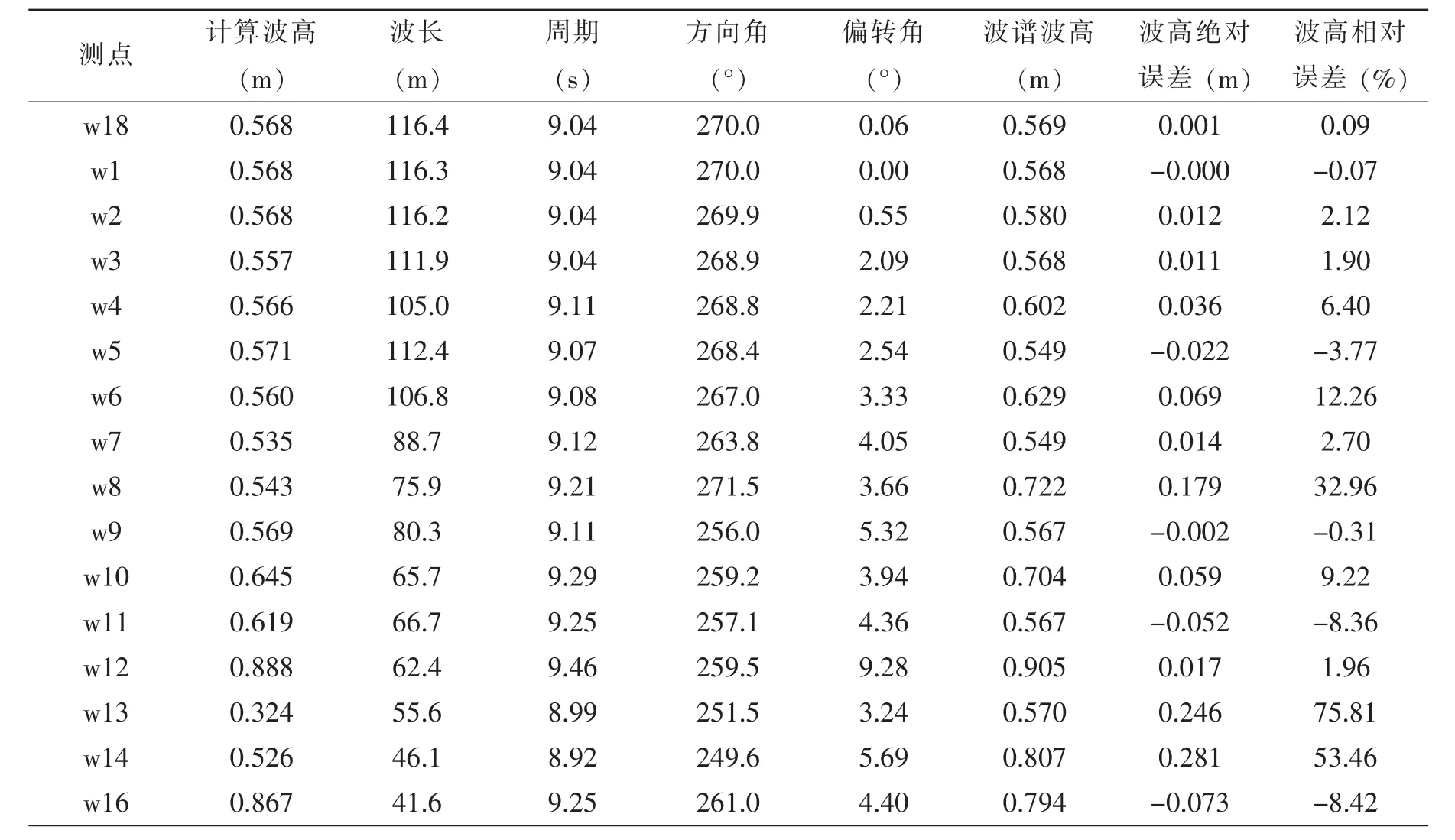
表4 工况EB401检测点的信息以及与试验的比较Tab.4 Information of detection points and compared with the experiment both under work condition EB401

表5 工况EB402检测点的信息以及与试验的比较Tab.5 Information of detection points and compared with the experiment both under work condition EB402

表6 工况EB403检测点的信息以及与试验的比较Tab.6 Information of detection points and compared with the experiment both under work condition EB403

表7 工况EB501检测点的信息以及与试验的比较Tab.7 Information of detection points and compared with the experiment both under work condition EB501

3.2 波谱误差分析

图4-7给出了不规则波的四种工况的一维波谱对比，其中左边为仿真结果，右边为试验结果。

从图4可以看出，仿真与试验在入口w18处的波谱完全一样，在w2处的接近，在w6处的波峰值有一定的差别，w10处的波形也比较接近，但是试验中w14处的波谱除了在0.1 Hz处有一个峰值外，在0.2 Hz处又出现一个较大峰值，导致试验中w14处的波高偏高，为0.807 m，而仿真中的波高要低于入口w18处的波高，为0.526 m，因此导致w14处试验与仿真的波高误差超过了50%。

图4 工况EB401观察点上的一维波谱对比Fig.4 Comparison of simulation and experiment of one-dimensional wave spectrum on observation points under work condition EB401

图5 工况EB402观察点上的一维波谱对比Fig.5 Comparison of simulation and experiment of one-dimensional wave spectrum on observation points under work condition EB402

从图5可以看出，仿真与试验在w18处的波谱完全一样，在w2处的接近，在w6处定性一致，而w10处和w14处的波谱在频率大于0.2 Hz处仍较大。

从图6可以看出，无论是仿真还是试验，w2、w6、w10处的波谱与w18处的波谱接近。类似工况EB401，w10处试验波谱在频率0.17 Hz处出现第二个较大峰值，导致试验与仿真的波高误差超过50%。在w14处试验与仿真的波谱定性一致，但是试验中在频率大于0.1 Hz范围内仍存在一定的能量，尽管试验和仿真在该处的波高接近，但是仿真波谱在0.08 Hz处的峰值要大于实验值。

从上面的分析可以看出，试验波谱与仿真波谱定性一致。但试验中w10和w14处的波谱存在两个明显的波峰，对于频率较大的波峰仿真中未出现。由于第二个峰值的出现，导致了试验与仿真的误差较大。

从图7可以看出，仿真中除了w14位置处的波谱明显小于入口w18处的波谱外，w2、w6处的波谱与w18处很接近，特别是w2处的波谱与w18处几乎重合。然而试验中w2处的波谱要明显高于w18处的波谱，而w6处的波谱明显小于w18处的波谱，因此导致w2处的波高实验与仿真有一定的误差。可能认为w6处的波谱不正确，试验报告中并未给出在该处测量的波高。w10和w14的波高对于试验和仿真是定性一致的，但试验中w10处的波谱在0.17 Hz处存在第二个峰值。

图6 工况EB403观察点上的一维波谱对比Fig.6 Comparison of simulation and experiment of one-dimensional wave spectrum on observation points under work condition EB403

图7 工况EB501观察点上的一维波谱对比Fig.7 Comparison of simulation and experiment of one-dimensional wave spectrum on observation points under work condition EB501

4 结 论

实际海域中的波为不规则波浪，本文对5种不规则波工况结果分析。从计算仿真结果来看，除了EB401的入射波波高较小时在w13和w14两点上试验和仿真的误差较大，其它工况和检测点上的波高相对误差绝大部分在10%左右。此外，当入射波高较大时，检测点上波高的相对误差较小。

在WAVEWATCH-III中，海底深度在以下5个方面对波浪演化存在影响：（1）波长修正；（2）海底壁面摩擦；（3）非线性作用；（4）碎波；（5）限幅值。其中第一项是水波满足的色散关系进行波长修正，第二至第四项通过模型源项来计算，第五项是水波假设理论的限制，在WW3计算过程中，有效波高限制在波长的12%以下，而波长又由色散关系与水深密切相关，这5个方面的影响随波高的增加而增加。而实际情况中，对于海底水深较浅而波高又较大时，波浪往往会漫过浅摊，在浅滩处的水深会有一个明显的抬升，形成壅水，而且此时波浪的传播不一定是按照正弦波的形式传播，水波理论假设不一定成立。因此采用WAVEWATCH-III仿真时，对于海底水深较浅而波高又较大的情况存在一定误差，而在实验与仿真的比较中，就会出现浅滩测点上的波高误差偏大（如w13和w14点）。在WAVEWATCH-III仿真中，如何合理对波长进行修正、如何定义浅滩的壁面摩擦系数、非线性模型和碎波模型、如何考虑浅滩中水深提高而改进限幅值的方法需要进一步的研究。

致谢

本研究由 973 项目 2013CB036101，国家自然科学基金（51379033；51379030；51239002；51221961），中央高校基本科研业务费专项资金（DUT15LK43，DUT15LK32），高科技船舶资助的项目（2016）22资助完成。

[1]Feng H,Vandemark D,Chapron B,et al.Use of a global wave model to correct altimeter sea level estimate[J].Geo Science and Remote Sensing Symposium,2004(4):2738-2741.

[2]Strauss D,Castelle B,Browne M,et al.Empirical estimation of near shore waves from a global deep-water wave model[J].IEEE Geo Science and Remote Sensing Letters,2006,3(4):462-466.

[3]齐义泉,朱伯承,施 平,等.WAVEWATCH-III模式模拟南海海浪场的结果分析[J].海洋学报,2003,25(4):1-9.Qi Y Q,Zhu B C,Shi P,et al.Analysis of significant wave heights from WWATCH and TOPEX/Poseidon Altimetry[J].Acta Oceanologica Sinca,2003,25(4):1-9.

[4]李明悝,侯一筠.利用Quick SCAT/NCEP混合风场及WAVEWATCH-III模拟东中国海风浪场[J].海洋科学,2005,29(6):9-12.Li M L,Hou Y J.Simulating wind-wave field of the East China Seas with QuikSCAT/NCEP blended wind and WAVEWATCH[J].Marine Sciences,2005,29(6):9-12.

[5]Whitman G B,Wiley J.Linear and nonlinear waves[M].New York:John Wiley&Sons,1974.

[6]凌宏杰,王志东.近岛礁生产生活平台及浮式栈桥系统水动力性能模型试验[R].镇江:江苏科技大学,2014.Lin H J,Wang Z D.Model experiment on hydrodynamic responses of floating platform near island and floating pier[R].Zhenjiang:Jiangsu University of Science and Technology,2014.

[7]Tolman H.User manual and system documentation of WAVEWATCH-III version1.18 NOAA/NCEP Tech[R].Note 166,1999:110.

[8]Tolman H,Booij N.Modeling wind waves using wavenumber-direction spectra and a variable wave number grid[J].Global Atmosphere and Ocean System,1998(6):295-309.

[9]Han S L.Evaluation of WAVEWATCH-III performance with wind input and dissipation source terms using wave buoy measurements for October 2006 along the east Korean coast in the East Sea[J].Ocean Engineering,2015(100):67-82.

[10]Tolman H.The numerical model WAVEWATCH:A third generation model for the Hind easting of wind wave son tides in shelf seas[R].Communication on Hydraulic and Geo technical Engineering,Delhi University of Technology,1989(2):89.

[11]Wittmann P A.Implementation of WAVEWATCH III at fleet numerical meteorology and oceanography center[J].OCEANS,MTS/IEEE Conference,2001(3):1474-1479.

[12]Hanson J L,Tracy B A,Tolman H L,Scott R D.Pacific hindcast performance of three numerical wave models[J].Journal of Atmospheric and Ocean Technology,2009(26):1614-1633.

[13]Tolman H,Balasubramaniyan B,Burroughs L D,et al.Development and implementation of wind-generated ocean surface wave models at NCEP[J].Weather and Forecasting,2002,17(4):311-333.

[14]梅强中.水波动力学[M].北京:科学出版社,1983.Mei Q Z.Wave dynamics[M].Beijing:Science Press,1983.

[15]文圣常,余宙文.海浪理论与计算原理[M].北京:海洋出版社,1984.Wen S C,Yu Z W.Wave theory and calculation principles[M].Beijing:China Ocean Press,1984.

[16]高加云.波浪谱数学模型初步应用研究[D].南京:河海大学,2006.Gao J Y.Rudiment research in application of spectral models for wind-waves[D].Nanjing:HoHai University,2006.

[17]Miles J W.On the generation of surface waves by shear flows[J].Fluid Mech,1957(3):185-204.

[18]林建国,邱大洪,邹志利.新型Buossinesq方程的进一步改善[J].海洋学报,1998,20(2):113-119.Lin J G,Qiu D H,Zou Z L.Further improvement of new Boussinesq-type equations[J].Acta Oceanologica Sinca,1998,20(2):113-119.

[19]郭衍游,侯一筠,杨永增,等.利用WAVEWATCH-III建立东中国海区域海浪同化系统[J].高技术通讯,2006,16(10):1092-106.Guo Y Y,Hou Y J,Yang Y Z,et al.To build a regional ocean wave data assimilation system of eastern China seas with WaveWatch III[J].Chinese High Technology Letters,2006,16(10):1092-1096.