一种考虑尾空泡影响的航行体流体动力数值仿真计算模型
高 勇,裴金亮,鲍文春
(1.海军驻航天科技集团公司第一研究院军事代表室,北京100076;2.北京宇航系统工程研究所,北京100076)
0 引 言
潜射导弹、鱼雷、水雷等水下垂直发射航行体在水下运动过程中所受的流体力是弹道或控制系统的主要输入参数,关系到航行体弹道稳定性、操控性或航程等总体参数,是各类型航行体设计的关键参数。航行体所受流体动力主要取决于流场性质、航行体流体动力外形以及相对流体的运动。目前,利用水下运动平台垂直发射航行体大多采用冷发射,即利用高压燃气将航行体弹射出筒,然后航行体依靠惯性穿越自由水面,发射过程可分为三个阶段:出筒段、水中航行段和出水段。这种发射方式下,在航行体尾出筒后,发射筒内高压燃气会在航行体尾部形成附着尾空泡[1-2]。由高压燃气组成的尾空泡不仅改变航行体受力,还影响了局部流场特征,见图1所示。尾空泡的形成演化过程对航行体水动力特别是轴向受力存在较大影响。
在水下航行体设计过程中,通常将流体动力分为位置力、阻尼力和惯性力三个部分。迄今为止,还难以用理论计算或缩比模型试验的方法直接获得包含上述所有因素的总流体动力,只能在各种假设和简化下,把流体动力分解成若干部分,分别由计算或试验的手段获得[3],然后综合成总流体动力,供航行体载荷设计及水弹道设计。航行体水弹道设计的主要目的在于获取航行体水下运动弹道参数变化规律,以确保航行体出水后的姿态控制要求。全湿流状态下,垂直发射航行体运动规律理论计算的关键在于准确获取水动力,包括定常水动力、惯性力、俯仰阻尼力等。
本文提出了一种考虑尾空泡影响的航行体定常水动力特性计算模型,分析了尾空泡对航行体定常位置力及旋转导数等的影响。采用所建立的尾空泡影响模型,对典型外形水下航行体水动力系数进行计算。将计算获得的流体动力代入理论弹道预示模型,获得的航行体水中运动规律与对应工况下缩比模型弹射试验规律一致性较好。

图1 水下航行体垂直发射尾空泡发展演化过程典型物理景象Fig.1 Physical scene of evolution process of tail-bubble during underwater vehicle vertical launching
1 计算模型
1.1 尾空泡模型
依据水下航行体缩比模型弹射过程景象及相关文献资料[4-5],在对航行体水下定常力进行计算求解时,考虑了一定形态的尾空泡影响。本文研究中,将初始航行体尾空泡假设成半椭圆形状的空泡(与出筒后的空泡形状相似),见图2所示。其中椭圆短半轴a=0.5D;椭圆长半轴b=αL,α为某一常数,本文中α取值为0.2。
1.2 位置力计算模型
对航行体定常水动力特性进行设计时,本体坐标系与航行体固连,参考点选在航行体质心位置,ox1轴与航行体纵轴重合指向前方,oy1轴位于航行体纵对称面内与ox1轴垂直指向上方,oz1轴与ox1y1平面垂直并与ox1轴和oy1轴构成右手系。

图2 考虑尾空泡影响航行体定常水动力计算示意图Fig.2 Simulation model when considering the effect of tail-bubble on steady hydrodynamics of underwater vehicle

图3 航行体本体坐标系Fig.3 The sketch of body coordinate system
计算域形式及边界条件定义见图4所示。对于水下低速运动问题,为使全计算域流场充分发展,航行体水动力系数稳定,特征尺寸L1、L2、L3均取为20D(D为航行体圆柱段直径),若计算涉及大攻角工况,需根据实际情况对计算域尺寸进行调整。

图4 计算域、边界及网格Fig.4 The scales of the calculation domain,boundary conditions and structured grids
全计算域采用分区结构化网格,航行体壁面第一层网格高度取0.2 mm,对尾空泡区域网格进行了加密处理,远场网格最大尺寸控制在100 mm以内。
1.3 旋转导数计算模型
基于FLUENT软件平台,采用动坐标系的方法,令航行体以攻角α绕指定圆心做匀速圆周运动,航行体质心与圆周运动圆心距离为R,转动角速度为ωz1,则匀速圆周运动线速度为V=Rωz1,见图5所示。在本体坐标系下Vx1=Vcosα、Vy1=Vsinα,航行体所受到的流体力有如下表达式。

通过开展航行体定速圆周运动下的数值计算,可求得一系列指定攻角α和无量纲旋转角速度下的法向力N和俯仰力矩M。上式(1)、(2)等号右侧变量均为已知,由此可求得
由于 λ11Vωz1cosα 项和 λ26Vωz1cosα 项内均含有ωz1,因此在弹道计算中通常将含有λ11的λ11Vωz1cosα项记入内, 将含有 λ 的 λVωcosα 项记入2626z1内。和的计算公式即为:
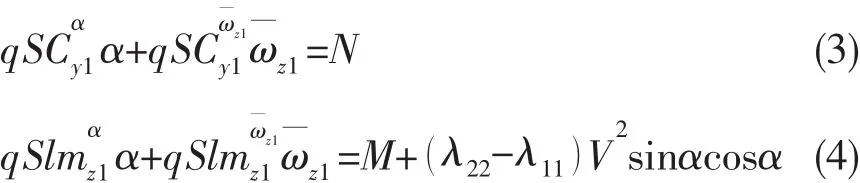

图5 旋转导数计算示意图Fig.5 The sketch in calculation of dynamic derivative
1.4 控制方程及求解器设置
对航行体水动力特性进行仿真计算时采用基于压力的隐式求解器,计算域内的流体选为水。采用SST四方程湍流模型[6],压力速度耦合方法选用SIMPLEC格式,压力项求解格式选用Body Force Weighted格式,流场控制方程选用二阶精度。
计算采用的来流速度条件V0及压力条件P0需保证除尾空泡区域的流场外不发生空化等多相流现象。提取航行体水动力系数时选用的参考值为:参考长度为航行体轴向长度;参考面积为航行体柱段横截面积;参考速度与速度入口值相同;力矩参考点选为航行体质心。
2 计算结果分析
2.1 尾空泡对位置力的影响
有、无尾空泡模型仿真获得的航行体轴向力系数对比情况见图6所示。有、无尾空泡影响对航行体头部及柱段部分的轴向力差异不大,都有随着来流攻角增加而减小的趋势;尾空泡的存在引起的尾部附加轴向力与航行体头部区域及柱段区域合力相当,由于尾空泡的存在引起的附加轴向力有随着来流攻角增加而增大的趋势。
考虑尾空泡影响后,航行体总的轴向力系数较不考虑尾空泡影响下明显减小,总的轴向力系数约为0.14,且在不同攻角状态下差异不大,不同攻角下的航行体总的平均轴向力系数与缩比模型弹射试验辨识结果(总的轴向力系数)基本相当,见图7所示。
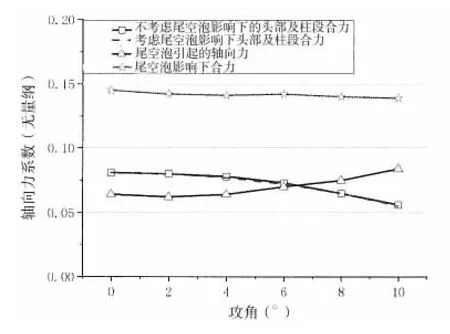
图6 有、无尾空泡模型对轴向力系数的影响对比Fig.6 The effect of tail-bubble model on the axial force coefficient
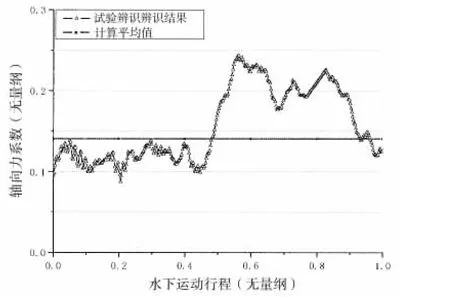
图7 试验辨识轴向力系数与计算结果比较Fig.7 The contrast of change law of the axial force coefficient identified by experiments and numerical calculation
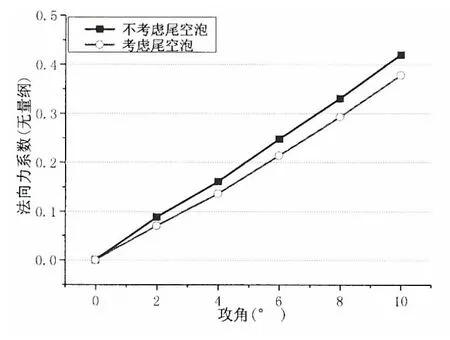
图8 有、无尾空泡模型对法向力系数的影响对比Fig.8 The effect of tail-bubble model on the normal force coefficient

图9 有、无尾空泡模型对俯仰力系数的影响对比Fig.9 The effect of tail-bubble model on the pitch moment coefficient
有、无尾空泡影响下的航行体法向力系数和俯仰力矩系数对比情况分别见图8、图9所示。结果表明,有、无尾空泡影响下,航行体法向力系数和俯仰力矩系数随来流攻角变化规律基本一致,均随来流攻角线性增加。在本文建立的尾空泡模型影响下,航行体法向力系数较不考虑尾空泡的模型减小10%~20%,俯仰力矩系增大约10%,对航行体水下俯仰姿态不利。随着来流攻角的增大,尾空泡模型对法向力系数和俯仰力矩系数的影响逐渐减弱,见图10、图11所示。

图10 尾空泡引起的法向力系数随攻角减小规律Fig.10 The rule of the normal force coefficient induced by tail-bubble
2.2 尾空泡对旋转导数的影响
有、无尾空泡影响下的航行体附加力系数和俯仰阻尼力矩系数对比情况见图12、图13所示,考虑尾空泡影响后,附加力系数对来流攻角的敏感程度减弱,航行体的附加力系数减小,最大减小量约为20%。俯仰阻尼力矩系数及变化规律与无尾空泡计算模型差异不大。

图12 有、无尾空泡模型对附加力系数的影响对比Fig.12 The effect of tail-bubble model on the additional force coefficient
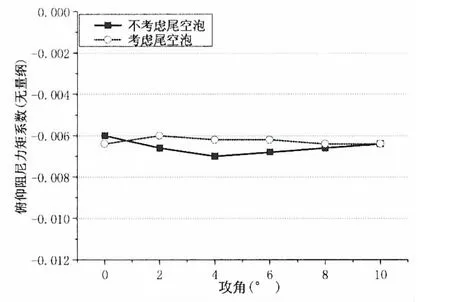
图13 有、无尾空泡对俯仰阻尼力矩系数的影响对比Fig.13 The effect of tail-bubble on the pitch damping moment coefficient
2.3 尾空泡对流场及参数的影响
航行体在不同攻角及圆周运动状态下,尾空泡的形态明显不对称。相比全湿流状态,尾空泡的存在明显改变了航行体尾部流场结构,航行体尾部附近的流体质点不再产生流动分离而形成涡结构,而是沿着尾空泡壁面向下游运动。尾空泡相当于航行体柱段物面向下游延伸形成可变形的均压收缩段后体,见图14所示。

图14 航行体尾部流场压力云图(攻角=4°)Fig.14 Contour of pressure on vehicle tail flow field
在不可压缩流动条件下,下游流场扰动会影响上游流场参数的变化。尾空泡的存在会改变航行体尾流场结构的同时也会对尾段物面压力分布产生影响,见图15所示。在全湿流条件下,航行体尾部存在流动分离所引起的低压区;在考虑尾空泡的情况下,航行体尾部流场压力相对较高,压力不对称性减弱,尾空泡会削弱尾段压力不对称性,使航行体尾部的分布旋转导数绝对值减小,见图16、图17所示。

图15 航行体迎背流面压力分布(攻角=4°)Fig.15 The distribution of pressure on vehicle’s surface

图16 分布附加力系数(攻角=4°)Fig.16 Pitch damping force coefficient distribution

图17 分布俯仰阻尼力矩系数(攻角=4°)Fig.17 Pitch damping moment coefficient distribution
3 尾空泡影响模型试验验证
利用本文建立的考虑尾空泡影响的定常水动力计算模型,可获得定常水动力参数。将参数代入航行体理论弹道预示模型,可对一定发射条件下航行体运动参数进行预示。将航行体典型运动规律与相同工况的缩比模型弹射试验数据进行对比,可考核本文的考虑尾空泡影响的航行体定常水动力计算模型。

图18 计算结果的水下运动规律与试验结果对比Fig.18 The comparison results of the underwater pitch parameters by numeration and experiment
航行体水下运动规律与试验结果对比情况见图18所示,计算获得的水下垂直发射航行体轴向运动规律、俯仰角速度和俯仰角变化规律与相同工况下模型弹射试验结果一致性较好。试验结果验证了本文建立的考虑尾空泡影响的航行体流体动力计算模型的正确性。
4 结 论
本文针对水下垂直发射航行体,建立了一种考虑尾空泡影响的定常水动力数值仿真计算模型,分析了尾空泡对轴向力、法向力、附加力及俯仰阻尼力矩的影响。应用本文建立的考虑尾空泡影响的模型及相应的流体动力求解方法,计算获取的流体力系数预示的航行体运动参数变化规律与模型弹射试验结果一致性较好,验证了计算模型的正确性,本文建立的考虑尾空泡影响的航行体流体动力计算模型具有一定的工程应用价值。
[1]刘志勇,颜 开,等.潜射导弹尾空泡从生成到拉断过程的数值模拟[J].船舶力学,2005,9(1):43-50.Liu Zhiyong,Yan Kai,et al.Numerical simulation of the development process of a trailing cavity from generation to separation[J].Journal of Ship Mechanics,2005,9(1):43-50.
[2]李 杰,鲁传敬,等.附着空泡对潜射导弹弹道影响分析[J].导弹学报,2014,9(3):54-58.Li Jie,Lu Chuanjing,et al.Analysis on influence of attached cavity on trajectory of submarine launched missile[J].Journal of Ballistics,2014,26(3):54-58.
[3]荣建德.水下运载器性能的分析与设计[M].北京:国防工业出版社,2008:25-36.
[4]崔 可,陈 浮.航行体出筒以及水下运动的水动力研究[D].哈尔滨:哈尔滨工业大学,2012:35-45.
[5]权晓波,燕国军,等.水下航行体垂直发射尾空泡生成演化过程三维数值研究[J].船舶力学,2014,18(7):739-745.Quan Xiaobo,Yan Guojun,et al.Three-dimensional numerical study on the evolution process of tail bubble of underwater vehicle vertical launching[J].Journal of Ship Mechanics,2014,18(7):739-745.
[6]侯宝新,支希哲,等.基于SST湍流模型的圆盘空化器超空泡特性仿真分析[J].西北工业大学学报,2015,33(2):260-264.Hou Baoxin,Zhi Xizhi,et al.Numerical simulation on supercavity characteristics of disc cavitator based on SST turbulence mode[J].Journal of Northwestern Polytechnical University,2015,33(2):259-264.

