代理模型在水下航行体空泡压力预示的应用研究

张晓东，权晓波，王占莹

（1.海军装备部，北京 100841；2.北京宇航系统工程研究所，北京 100076）

0 引 言

水下垂直发射航行体在水下运动过程中表面会形成含气空泡，使得航行体流体动力呈现强非线性非定常特征[1]，并对航行体载荷和姿态造成重要影响。航行体表面空泡压力是航行体载荷和运动参数设计的基础，其特性的预示研究具有十分重要的意义。CFD方法是目前水下空泡绕流特征预示的主要研究手段之一，但该方法所需计算周期长、成本高，同时多相流数学模型局限性也对计算精度和可用性产生一定的影响。近年来，代理模型技术作为一种高效建模方法，为流体动力设计提供了可行的工程技术手段，是试验设计、统计方法、优化等多项技术的综合应用成果。权晓波等[2]采用代理模型方法对水下航行体头型优化设计进行了研究，有效提高了航行体头型多目标优化设计方法的效率；王惠等[3]基于代理模型开展了水下航行体空泡非定常发展预示方法研究，为空泡非定常发展设计提供了一种重要手段；马洋等[4]也开展了运载器头罩外形的代理模型方法优化设计研究，温庆国等[5]基于代理模型进行了鱼雷外形阻力的单目标优化，获得较为满意的鱼雷外形。

代理模型是指在不降低精度的情况下利用已知的有限样本点数据构造一个计算量小、计算周期短但计算结果与数值分析或是物理实验相近的数学模型。代理模型建立起输入参数到输出参数的快速响应系统，可减小计算周期、降低实验计算成本。代理模型方法种类较多，具有不同的特点且各有优劣，Fang和Wang等[6]介绍了插值型代理模型的模型精度评估方法，并将拟合型代理模型的误差评价函数应用于插值型代理模型中；Romero等[7]分析研究了响应面代理模型的模型精度评价方法，这些方法对拟合型代理模型都具有可借鉴之处。

空泡压力峰值和空间分布特征与众多物理因素相关，并且具有较强的非线性规律和特征。本文基于对空泡压力特征影响因素研究[8]，采用目前在工程应用上较为广泛的径向基神经网络、Kriging代理模型技术，分别建立了空泡压力特征代理模型，并通过对不同代理模型预示分析及与试验数据的比对，综合两种代理模型的理论优缺点，进行了基于空泡压力特征预示的代理模型的评估，为空泡绕流作用下航行体表面压力预示提供了有效的手段。

1 代理模型技术

1.1 径向基代理模型

径向基函数（Radial Basis Function，RBF）[9]模型是一种利用离散多元数据来拟合未知函数的方法。其基本原理是以典型的径向函数为基函数，以已知样本点与未知待测点之间的欧氏距离作为径向基函数的自变量，通过线性叠加径向函数构造出来的模型。

径向基函数模型方法就是，找寻函数f（x），x∈Rn来近似n维变量实值函数F（x），函数f（x）用φ（r）作为基函数，φ（r）是由x与每一个数据点xi的径向距离r决定的。该函数的基本思想是，首先确定一组样本点 x=（x1，x2，xi，…，xm）， （i=1，2，…，m ），然后以这些样本点为中心，以径向函数为基函数，通过这些基函数的线性叠加来计算待测点x处的响应值。通过欧氏距离，径向基函数可以很容易地把一个多维问题转化成以欧氏距离为自变量的一维问题。径向基函数的基本形式如下，对于自变量x，其响应值y可表示为：

式中：

径向基函数模拟一般可表达如下：

用上式作为预测模型时，它要满足如下的插值条件：

而后可以得到方程组：

式中：

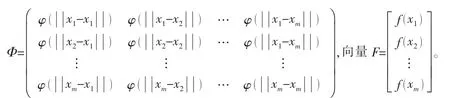
（4）式Φβ=F在样本点不重合，且函数φ（）r为正定函数时存在唯一解，即：

一个典型的RBF网络结构，它由一个输入层、一个隐含层和一个输出层组成，如图1所示。它反映了系统的多输入x∈Rn和多输出y∈Rn之间的函数关系：f:x→。输入节点只是传递信号到隐含层，输出节点通常是简单的线性函数。

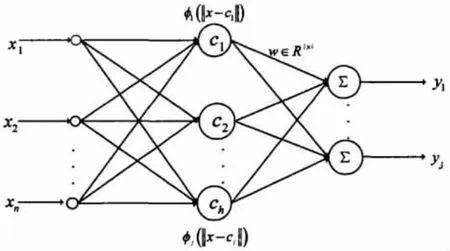
图1 径向基神经网络结构图Fig.1 Structure of RBF neural network

隐含层节点是由一种是通过局部分布的、对中心点径向对称衰减的非负非线性函数构成，常用的基函数有：高斯（径向基）函数、多二次函数、逆多二次函数、反射Sigmoid函数等。

本文应用的基函数是高斯（径向基）函数，其形式为：

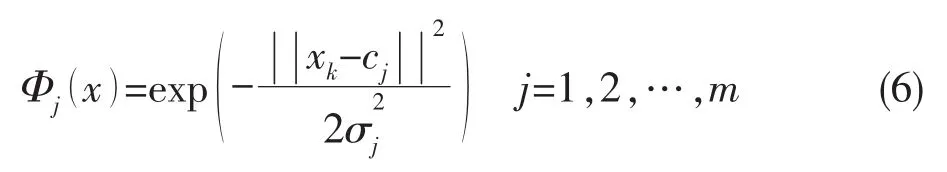
式中：cj为第j个隐藏层神经元的中心；σ2为高斯函数的标准差为xk与cj之间的欧几里得范数。

RBF神经网络的第j个输出可表示为：

式中：X为输入向量；为第j个隐藏层神经元到第i个输出层神经元的权值。整个RBF的性能取决于径向基函数的中心和权值的选择。

1.2 Kriging代理模型

Kriging代理模型是一种估计方差最小的无偏估计模型[3，10]。模型包含两部分：多项式和随机分布。

式中：β是回归系数，f（x）T是变量x的n阶多项式，随机分布的误差为z，其均值为0，方差为，具有如下统计特性：

式中：xi，xj为样本中的任意两点；R（ θ， x i，xj）是以θ为参数的相关模型，表示样本的空间相关性。 本文选取的高斯相关函数表达式为：

式中：xik，xjk是样本点xi，xj第 k 维元素。

对于m维初始样本点，其响应为Y，可得多项式F和相关矩阵R。对于一个待测点x的，可得多项表达式f和相关阵r，其响应值利用样本点xi的响应值Y线性加权叠加计算，即

在无偏性要求下，公式（11）预测模型产生的预测方差为：

C（x）与待测点和已知点间的相关性矩阵有关。由最小二乘估计可得：

拉格朗日方程求解上述方程取最小值时可得：

1.3 模型误差分析

代理模型需要另取样本点来验证模型的精度，以保证模型的有效性，本文模型误差评估主要采用如下方法：

（1）均方根差检验

模型预测点的均方根差为：

方差的估计值为σ2：

（2）平均绝对值相对误差检验

模型预测点的平均绝对值相对误差为：

（3）平均相对误差

模型预测点的平均相对误差为：

1.4 典型算例比较

Kriging模型是一种对空间数据求线性最优、无偏内插估计的一种插值方法，具备局部估计的特征，适应解决非线性程度较高问题。同时由于输入矢量各方向的核函数参数可以取不同值，所以Kriging既可以解决各项同性问题也可以解决各向异性问题。

径向基神经网络是以径向基函数为基函数，通过欧氏距离，径向基函数可以很容易地把一个多维问题转化成以欧氏距离为自变量的一维问题。并通过线性叠加构造径向基函数到输出的代理模型，其网络简单、映射能力强，相比于响应面和Kriging，是介于两者之间的一种方法。

响应面代理模型在给定输入输出的基础上，以数学多项式作为基函数通过最小二乘回归法来得到设计变量和响应间的映像关系，具有很好的可导性和良好的连续性，易寻优并且可以使用常规的优化方法求得极值，但是由于多项式本身对非线性问题的描述能力不足，在遇到非线性程度较高的问题时，模型的拟合预测效果往往不太理想，在多项式阶数较高时，还易出现过拟合的现象。

为了对比各种代理模型的实际拟合效果，将它应用到一个二维非线性测试函数中：

该函数具有连续起伏的性质，如图2所示。

图2 测试函数的原始曲面Fig.2 Original surface of test function

表1 基本代理模型的比较Tab.1 Comparison of different surrogate modles

对要建立的Kriging近似模型，选择二元二次多项式作为Kriging模型确定部分的函数类型，选择高斯函数作为变异函数；考虑各向异性的作用。本文通过拉丁超立方抽样方法分别选取40、100和200子样数三组实验，对于不同子样数量的实验设计，进行Kriging近似模型拟合。图3、图4分别给出了40和200子样数下Kriging模型模拟的非线性函数曲面，从图中可以看出基于40子样数的拟合结果与原函数结果差距十分明显，而200子样数下拟合结果则较好地还原了函数，各点的相对误差基本为零。

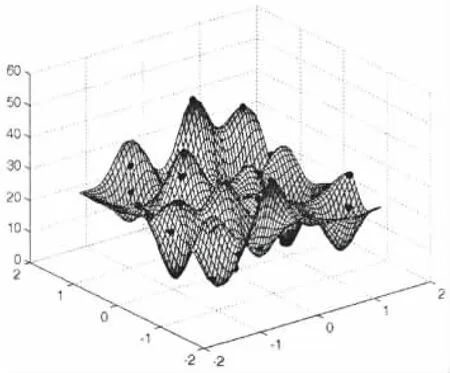
图3 40子样数Kriging模型的近似曲面 Fig.3 Approximately surface of Kriging surrogate method with forty samples

图4 200子样数Kriging模型的近似曲面Fig.4 The approximately surface of Kriging surrogate method with two hundreds samples

表2 不同子样数实验设计Kriging模型结果比较Tab.2 Comparison of the prediction of Kriging surrogate method with different samples

对于不同水平的实验设计，进行Kriging近似模型拟合。为了与原函数结果进行比较，误差取样点m取为31×31，其结果列于表2。由表2可见，用Kriging近似模型拟合的曲面完全满足精度要求，并且样本数量越多预示精度越高。

同样为了验证RBF的实际预示效果，同样利用（19）式测试函数进行检验。

图5 40子样数RBF模型的近似曲面Fig.5 Approximately surface of RBF surrogate method with forty samples

图6 200子样数RBF模型的近似曲面Fig.6 Approximately surface of RBF surrogate method with two hundreds samples

对要建立RBF近似模型，均方根选取默认值为0，神经元个数选择自适应，本文分别选取40、100和200子样数三组实验，进行RBF近似模型拟合。图5、图6分别给出了40子样数和200子样数RBF模型模拟的非线性函数曲面，从图中可以看出基于40子样数的拟合结果与原函数结果差距十分明显，尤其是在其边界处，拟合结果波动较为剧烈，从相对绝对误差以及均方根误差的结果可以发现，当样本点较少时，Krging的相对误差较小，且拟合结果波动较小。200子样数的拟合结果RBF和Kriging两种代理模型均较好地还原了函数，各点的相对误差基本为0。

表3 不同子样数实验设计RBF模型结果比较Tab.3 Comparison of the prediction of RBF surrogate method with different samples

表4 不同子样数实验设计响应面模型结果比较Tab.4 Comparison of the prediction of Response surface surrogate method with different samples

为了与原函数结果进行比较，误差取样点m取为31×31，其结果列于表3。由表3可见，用RBF近似模型拟合的曲面完全满足精度要求，并且子样数越多曲面精度越高。

同时采用5阶多项式响应面模型进行测试，拟合效果误差精度见表4。从误差分析可以看出，响应面模型无法复现（19）式的非线性函数。

基于以上三种模型对于测试函数的验证可以发现，当测试样本较少时，Kriging模型预示结果均方根差最小，响应面模型误差最大，随着样本数量的增加，RBF和Kriging均可以精确实现对函数的预测，误差基本为0，而响应面模型基本不能实现对测试函数的复现。

综上所述，从代理模型的对二阶非线性函数预测精度来看，随着样本数量的增加，RBF和Kriging代理模型均可以得到较为精确的结果。响应面模型对非线性程度较高的函数，基本不能获得理想的结果。当测试样本较少时，RBF拟合效果波动十分剧烈尤其是边界附近，因此平均相对误差和均方误差相对于Kriging代理模型均较大；Kriging整体的波动不是十分剧烈，整体误差较低。

2 空泡压力代理模型建模研究

航行体水下运动过程中，在来流作用下沿航行体轴向不断发展，空泡末端闭合区扫过航行体表面，不同时刻空泡闭合区压力沿航行体轴向空间分布，如图7所示。可以看出，空泡区内部为稳定泡内压力，压力保持常值，空泡区末端回射流作用区域，航行体表面压力急剧上升至最大压力而后缓慢降低至环境压力，这是由于空泡闭合时回射流的速度效应和压力效应引起的压力升高[11]。

图 7 不同时刻（T0、T1和 T2）空泡闭合区压力沿航行体轴向空间分布特征Fig.7 Axial pressure distribution of underwater vehiclein at different moment

2.1 空泡回射压力模型

目前非定常空泡回射流闭合区域压力的理论研究极少见，更没有可直接应用于工程的闭合区域压力的计算公式，空泡截面独立膨胀原理[12]只能近似解决空泡形态的计算，而不能预报空泡尾部闭合区域中作用于物体的流体动力。已有的研究应用势流理论分析了重力场中非定常轴对称垂直空泡回射压力峰值，证明了非定常空泡闭合区域的最大压力点位置就是压力坐标系中的驻点[13]，推导了非定常空泡闭合区域最大压力的公式。从最近关于空泡闭合压力影响因素的研究[8]表明，空泡闭合区回射最大压力的主要影响因素有四项，分别为导弹运动动压、当地静压、泡内压力以及尾空泡干扰压力，可以根据这四项主要影响因素建立最大压力代理模型。

分别采用RBF和Kriging代理模型技术建立影响因素和空泡回射最大压力之间的关系，以航行体表面密集分布的水动外压作为研究对象，通过获取在水下发射过程中航行体表面测量的空泡闭合区回射压力最大值以及相应状态下的影响因素，建立空泡闭合区最大压力代理模型。考虑到实际工况条件的取值范围，选取样本工况和预测工况如表5所示，样本工况在发射条件取值范围内分布较均匀，预测工况选取不同于样本工况的点。

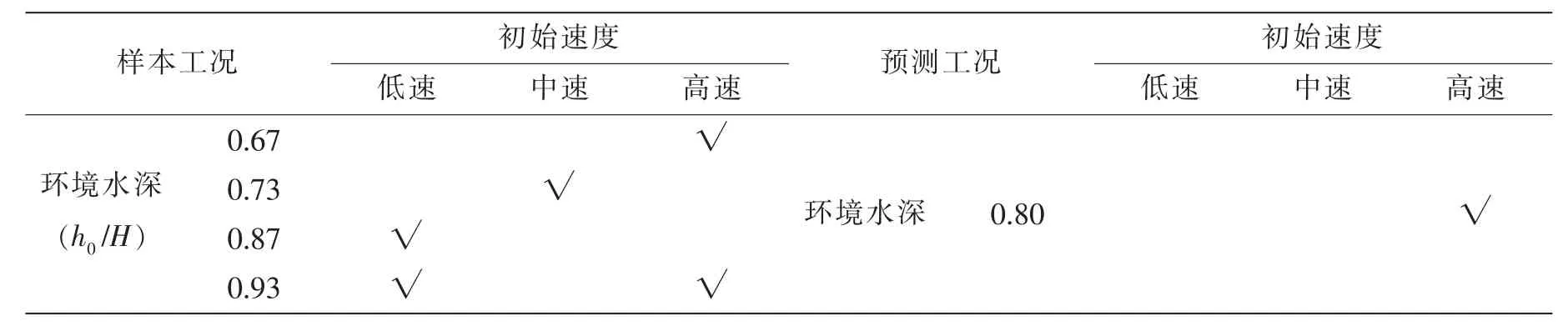
表5 空泡闭合区最大压力代理模型样本工况和预测工况Tab.5 Sample points and predicted points of surrogate modle

RBF和Kriging代理模型计算获得空泡闭合最大压力与试验结果对比见图8和图9，由图中可以看出，两种代理模型都可以预示空泡闭合回射压力最大值的变化趋势，从误差量值分析来看，Kriging代理模型相对于RBF代理模型预示精度更高。

图8 Kriging代理模型计算回射压力峰值与试验结果对比Fig.8 Comparison between prediction of Kriging surrogate model and test of the pressure of cavity closure area in space

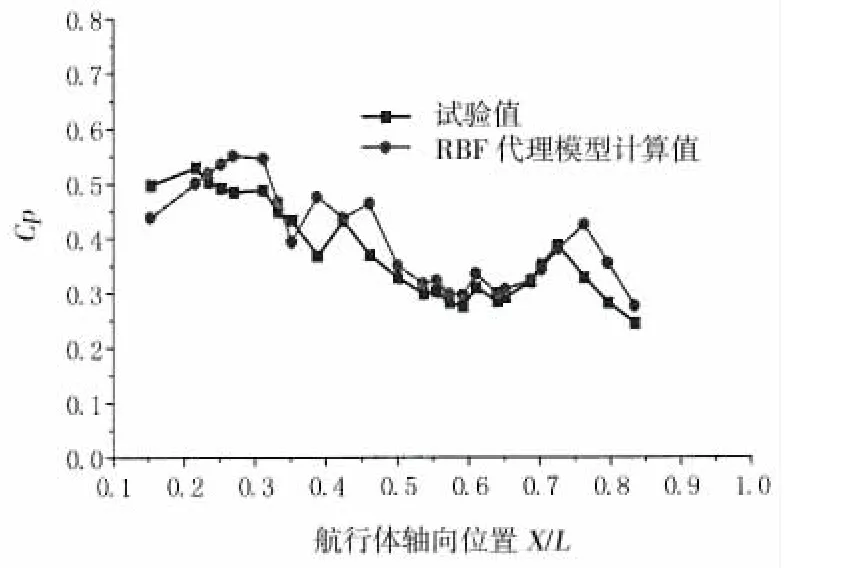
图9 RBF代理模型计算回射压力 峰值与试验结果对比Fig.9 Comparison between prediction of RBF surrogate model and test of the pressure of cavity closure area in space

表6 最大压力代理模型预测误差Tab.6 Comparison between prediction error of different surrogate models of the pressure peak of cavity closure area

2.2 空泡压力波形描述方法

根据空泡闭合区压力空间分布特征，见图10，将高斯脉冲函数参数赋予物理意义，构造沿航行体轴向空间分布的波形函数，实现空泡闭合区压力分布特征的模型化。其中a和b共同决定脉冲峰值的大小。δ表征脉宽值，δ越大脉宽越大；系数n表征曲线丰满程度上升和下降速率，n越大曲线上升、下降变化越急剧。通过确定高斯脉冲函数参数的物理意义，调整函数相关系数改变曲线形式，达到与空泡闭合区压力波形一致的分布特征。

基于试验结果由于波形上升沿和下降沿的值不同且均不为零，需要将空泡压力波形函数分段进行描述，在空泡闭合区压力最大值点处进行分段，上升段表达式为下降段表达式为系数b1、b2分别表征空泡内压力和当地环境压力；系数a1、a2与b1、b2共同决定空泡闭合区压力最大值；丰满度系数n1、n2的大小通过与试验结果比对确定，上升段、下降段取值分别为2 和 0.8；系数 δ1、δ2与脉宽 Dx1、Dx2，丰满度系数 n1、n2之间的关系为为常数。

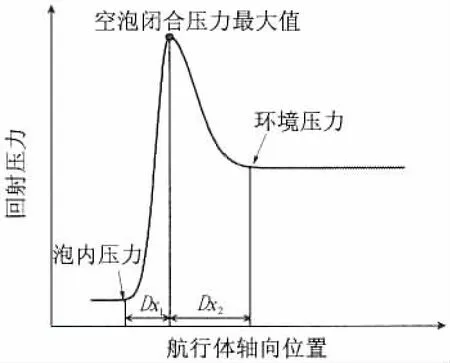
图10 空泡闭合区压力波形相关参数物理意义Fig.10 The physical significance of pulse function parameters of pressure of cavity closure area

从图11可以看出，应用上述高斯函数表达式构造空泡闭合区域压力在航行体轴向空间分布波形，空泡压力波形计算值与试验数据吻合较好，表明此方法可以用于预示空泡闭合压力波形的分布。

2.3 基于代理模型的空泡压力预示

空泡压力波形代理模型主要是针对表征脉宽的物理量δ进行建模，采用与回射闭合区压力最大值相同的影响因素，建立回射压力空间分布脉宽代理模型进行预示，其过程与空泡闭合区最大压力预示方法一致。

基于代理模型预示的回射压力峰值和回射压力空间分布波形脉宽结果，从试验数据中提取空泡末端位置、泡内压力、环境压力等状态参数；利用高斯函数复现空泡回射压力沿着弹体表面的分布，从图12中可以看出，预示结果可以较好地预示空泡闭合区域压力的空间分布特征和非定常变化趋势。

图11 空泡闭合区压力波形描述方法与试验对比 Fig.11 Comparison between calculation result and test of pressure wave form

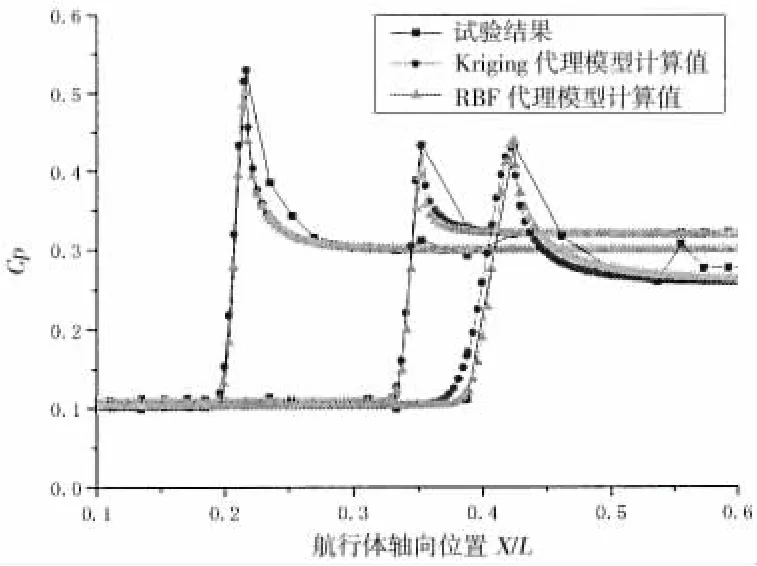
图12 空泡闭合区压力分布计算值与试验对比Fig.12 Comparison between prediction and test of the pressure of cavity closure area in space

3 结 论

本文应用RBF代理模型和Kriging代理模型分别建立了影响因素与空泡压力空间分布之间的代理模型，并开展给定工况下空泡压力的预示研究，通过与试验数据比对验证了预示方法的正确性，并针对两种代理模型的预示误差进行了代理模型预示精度评估。

（1）通过对二阶非线性典型测试函数的预示结果表明，RBF和Kriging代理模型在样本数量较多时，均可以得到较为精确的预示结果，响应面模型则难以预示非线性程度较高的函数；样本数量较少时，RBF拟合效果波动十分剧烈，尤其在函数边界位置，预示误差相对于Kriging代理模型较大；

（2）基于RBF代理模型和Kriging代理模型建立的空泡闭合压力最大值与影响因素的关系，可以较准确预示空泡闭合回射压力最大值变化趋势，Kriging代理模型预示精度更高；

（3）空泡压力空间分布波形可通过高斯函数表达式来近似，并且通过两种代理模型建模研究，可以实现空泡闭合压力空间分布的预示。

[1]Knapp R T,Daily J W,Hammitt F G.Cavitation[M].Mcgraw-Hill Book Company,1970:63－139.

[2]权晓波,王 惠,魏海鹏,等.基于代理模型的水下航行体头型优化设计方法研究[J].船舶力学,2016(10):1262-1268.Quan Xiaobo,Wang Hui,Wei Haipeng,et al.Configuration optimization design of underwater vehicle based on surrogate model[J].Journal of Ship Mechanics,2016(10):1262-1268.

[3]王 惠,权晓波,魏海鹏.水下航行体空泡非定常发展预示方法研究[J].导弹与航天运载技术,2017(2):1-6.Wang Hui,Quan Xiaobo,Wei Haipeng.Prediction method on unsteady cavity development of underwater vehicle[J].Missiles and Space Vehicles,2017(2):1-6.

[4]马 洋,王丹丹,杨 涛,等.基于代理模型的运载器头罩外形优化设计[J].航空动力学报,2014,29(1):192-198.Ma Yang,Wang Dandan,Yang Tao,et al.Optimization design of shroud configuration of trans-porter based on surrogate model[J].Journal of Aerospace Power,2014,29(1):192-198.

[5]温庆国,宋保维,王 鹏,等.改进的Kriging近似方法及其在鱼雷外形优化中的应用[J].上海交通大学学报,2013,47(4):613-618.Wen Qingguo,Song Baowei,Wang Peng,et al.An improved kriging approximation and its application to shape design optimization of torpedo[J].Journal of Shanghai Jiao Tong University,2013,47(4):613-618.

[6]Fang H,Wang Q,Horstemeyer M F.Model accuracy evaluation of compactly supported RBFs[C]//AIAA.Newport,Rhode Island,2006.

[7]Romero V J,Slepoy R,Swiler L P,et al.Error estimation approaches for progressive response surfaces[C]//AIAA.Austin,Texas,2005.

[8]王 惠.基于代理模型的潜射导弹空泡绕流水弹道预示方法研究[D].北京:北京宇航系统工程研究所,2017.Wang Hui.Research on the design method of under-water trajectory of submarine-launched missile with cavity based on surrogate model[D].Beijing:Beijing Institute of Astronautical System Engineering,2017.

[9]李 坚.代理模型近似技术研究及其在结构可靠度分析中的应用[D].上海:上海交通大学,2013.Li Jian.Study of surrogate model approximation and surrogate-enhanced structurel reliability analysis[D].Shanghai:Shanghai Jiao Tong University,2013.

[10]Gano S E,Kim H,Brown D E.II.Comparison of three surrogate modeling techniques:datascape,Kriging,and Second order regression[C].11th AIAA/ISSMO Multidisciplinary Analysis Conference,6-8 Sep,2006.AIAA-2006-7048.

[11]魏海鹏,郭凤美,权晓波.潜射导弹表面空化特性研究[J].宇航学报,2007,28(6):1506-1509.Wei Haipeng,Guo Fengmei,Quan Xiaobo.Research on cavitation of submarine launched missile’s surface[J].Journal of Astronautics,2007,28(6):1506－1509.

[12]张学伟,张 亮,王 聪,等.基于Logvinovich独立膨胀原理的超空泡形态计算方法[J].兵工学报,2009,30(3):361-365.Zhang Xuewei,Zhang Liang,Wang Cong,et al.A calculation method for supercavity shape based on the Logvinovich independence principle of the cavity section expansion[J].Acta Armamentarii,2009,30(3):361－365.

[13]陈玮琪,王宝寿,易淑群,等.非定常空泡闭合区域最大压力的理论研究[J].力学学报,2012,44(4):701-708.Chen Weiqi,Wang Baoshou,Yi Shuqun,et al.A theoretical investigation on the maximum pressure of the unsteady cavity closure position[J].Chinese Journal of Theoretical and Applied Mechani,2012,44(4):701-708.