SBD技术在“探索一号”科考船线型设计中的应用

倪其军，李胜忠，阮文权 ，侯小军，杨 磊

（1.江南大学 环境与土木工程学院，江苏 无锡 214122；2.中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

随着全球海洋开发事业的发展，海洋资源勘探、考察等工作对科考船的功能要求和技术要求越来越高。据有关数据统计全球有40多个国家或地区拥有自己的海洋科学考察船，数量超过500艘，而且一些发达国家的海洋考察船及海洋勘探技术非常先进。科考船也在向综合性、现代化和大型化方向发展。为了迅速提升我国深海科考能力，并为4 500 m载人潜水器提供搭载平台，在原工程作业船“海洋石油299”的基础上，开展“探索一号”科考船重大改造设计，提高船舶技术性能和安全可靠性，使其具备支持4 500 m载人潜水器、深海科学考察、深海装备试验的能力。本文主要介绍“探索一号”科考船的船型设计过程及其所采用的当前先进的基于仿真设计（Simulation Based Design，SBD）的船型设计技术。

SBD技术是随着CFD技术、CAD技术以及最优化技术的发展，而出现的一种新的以目标驱动设计的构型设计模式。它将CFD技术系统地融入优化过程，并结合最优化理论与几何重构/变形技术，实现对优化目标的直接寻优。其基本原理与优化设计流程如图1和图2所示。

图1 SBD船型设计原理Fig.1 SBD-based hullform design optimization environment

图2 典型自动设计流程Fig.2 Typical automated design process

国外在以减阻为目标的SBD船型优化设计方面开展了大量的研究工作，特别是对船体几何重构技术、多目标全局优化技术、近似技术、综合集成技术（并行计算）等关键技术进行了较为系统的研究，也取得了诸多成果。INSEAN水池的Campana和Peri等[1]以DTMB5415船模作为优化对象，对多目标全局优化算法和近似技术（变逼真度模型）以及船体几何重构方法（分别采用Bezier Patch和基于CAD的几何重构方法）进行了较为详细的研究。对优化设计方案的模型试验验证结果表明：优化设计方案的总阻力比初始设计方案减小5.23%。为了推进SBD技术能够面向实际的工程应用，Peri和Campana等[2]以解决高精度CFD数值计算带来的响应时长和计算费用问题为目标，对简约策略—近似技术进行了详细的总结和研究。Yang等[3]基于NURBS船体几何变形方法开展了船舶球艏水动力优化设计。

国内近几年在该领域的研究也取得很大的进步，许多关键技术问题也已取得突破。中国船舶科学研究中心开展了众多以减阻为目标的船型优化设计研究工作：针对6 600DWT、44 600DWT等多型散货船开展了线型优化设计，减阻效果及推进效率提升十分显著[4-6]；以某舰船作为设计对象，开展了经济速度与设计航速下的多目标优化设计，结果表明最优方案与原方案在两个设计点的模型总阻力分别减小了5.5%和5.1%，且减阻效果得到了模型试验验证[7-9]。

本文首先介绍了探索一号科考船改型设计，采用基于RANS的数值评估方法对改型前后船舶阻力进行计算分析。之后，简要地阐述了SBD船型设计方法，并以改型方案为对象，采用SBD技术对其艏部线型进行了优化设计，并对设计结果进行了详细的对比分析。

1 艏部改型设计与阻力预报分析

1.1 艏部改型方案

“探索一号”科考船是在原多功能工程作业船“海洋石油299”的基础上改建而成，依据总体设计要求，仅保留原船尾半段船体，艏部线型重新设计。艏部改型设计方案与原船相比，长度增加了13.8 m，设计吃水由6.35 m变为5.50 m，排水体积增加了245.5 m3。改型前后船舶主尺度参数见表1。船体外形示意图如图3所示。

图3 原船与改型设计方案示意图Fig.3 The side view of original and redesign case

表1 船舶主尺度Tab.1 Principal dimensions of ship

1.2 改型设计前后阻力数值计算与分析

本文采用高精度的RANS方法对原型和设计方案的船舶模型阻力进行数值预报。湍流模型选用SST k-ω，自由面采用level-set方法处理。采用重叠网格技术，船体贴体网格与背景网格重叠，网格单元数量约为60万（一半计算域），其中第一层网格间距根据y+确定（y+平均约为50）。计算域及船体表面网格如图4和图5所示。

图4 计算域Fig.4 Computation region

图5 原船与改型设计方案表面网格Fig.5 The hull surface mesh of original and redesign case

表2 原船与改型设计方案阻力计算结果及比较Tab.2 Comparison of resistance components between the original and the redesign case

计算模型的缩比为1：15，分别计算了对应实船航速8 kns、10 kns、12 kns、14 kns和16 kns时的模型阻力。结果见表2，自由面兴波见图6～8。从表中可以看出：改型设计方案在对应实船航速Vs=8～16 kns时，模型阻力减小了2%～5%左右，实船总阻力分别减小了1%～5%左右，其中12 kns时，实船总阻力减小了2.9%，改型设计方案的排水量较原船增加4.1%。从兴波云图可以看出，改型方案的兴波波形与原船不同（船长的变化引起的），波幅明显小于原船。

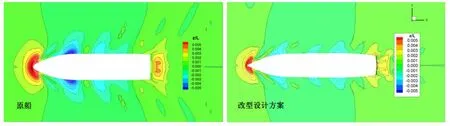
图6 原船与改型设计方案Vs=10.0 kns时的自由面波形云图Fig.6 Comparison of wave contours between the original and the redesign case(Vs=10.0 kns)

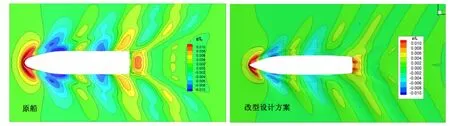
图8 原船与改型设计方案Vs=14.0 kns时的自由面波形云图Fig.8 Comparison of wave contours between the original and the redesign case(Vs=14.0 kns)

2 基于SBD技术的艏部线型优化设计

在改型设计方案的基础上，采用SBD船型设计方法以阻力最优为目标开展线型优化设计。首先对SBD船型设计方法进行简要的介绍，之后详细地描述了艏部线型优化设计过程及其结果分析。

2.1 船型SBD设计方法简介

SBD船型设计方法是以先进的CFD技术为依托，以超级计算机集群的高速计算能力为基础，结合船体几何重构与变形技术，并将其融入基于现代优化分析理论的设计流程，建立的一种崭新的源于严谨数理控制、基于知识化的船舶水动力构型设计模式。它是以船舶一项或多项水动力性能最优作为设计目标，在给定的约束条件和构型设计空间内，通过CFD数值评估技术和现代最优化技术实现船舶水动力构型的优化求解（逆问题求解），最终获得给定条件下的水动力性能最优的船型。

该设计方法具有如下特点：设计过程是目标驱动设计；设计依据是最优化理论；设计手段是先进CFD技术；设计质量是满足约束条件的最优设计。主要关键技术包括以下三个方面。

2.1.1 最优化技术

最优化技术是区别于经验设计、体现知识化船型设计的重要特征，是求解船型优化设计问题的科学方法和必要手段。最优化技术在整个优化设计流程中充当“指路器”：即为优化设计问题的求解提供科学方法，科学地指导最优解的搜索方向。其作用是快速、准确地搜索到构型设计空间中的全局最优解。

2.1.2 船体几何重构技术

船体几何重构技术是联系优化算法（设计变量）与船舶性能分析评估（目标函数）之间的桥梁和纽带，同时也是船型优化设计过程中的关键环节。在船舶优化设计过程中，必需首先对船体几何进行参数化表达，利用尽可能少的参数实现船体几何的重构，并且要建立船体表达参数与优化过程中设计变量之间的联系。船体几何重构技术在整个优化设计流程中充当“链接器”：其作用是自动生成尽可能多的设计方案；直接决定船型优化问题的设计空间“大小”。

2.1.3 船舶水动力性能预报评估技术

船舶水动力性能预报评估技术是建立船型优化问题数学模型的基础，是连接船体几何外形和优化平台的纽带。水动力性能的预报精度直接影响着优化设计结果的质量。用于船型优化设计的船舶水动力性能评估方法应该具备以下条件：预报精度尽可能高且稳定；预报结果对船体几何变化比较敏感，即具有较好的“分辨率”；计算响应快捷、高效。然而，精度高、“分辨率”好与计算响应快捷高效往往相互矛盾，这给水动力性能评估方法带来了非常苛刻的要求。本文采用基于RANS的CFD数值评估技术，已在多个船型设计中进行了应用[4，6，8-9]，能够满足上述要求。

2.2 艏部线型优化设计

2.2.1 目标函数及其评估方法

应用SBD船型设计方法对设计方案艏部线型进行优化设计，以船模（缩比λ=1：15）在Fn=0.203（即实船航速Vs=12 kns）时的总阻力最小作为优化目标，即：

优化设计过程中的阻力评估采用上节介绍的数值计算方法。

2.2.2 设计变量及约束条件

船体几何重构采用FFD方法，将船舯前部分装入控制体中，共选择十二组顶点，每组为一个设计变量共十二个设计变量，实现船体的自动变形与重构。排水量约束，船体湿表面积约束，船长、宽、吃水等主尺度参数保持不变。

2.2.3 优化算法

优化算法的选择对优化问题的求解至关重要，合适的优化算法不仅可以提高搜索效率，而且可以避免搜索陷入局部最优解，提高获得全局最优解的可靠性。本文采用基于随机搜索的粒子群优化算法（Particle Swarm Optimization,PSO）对船体线型优化设计问题进行求解。该算法在船舶水动力性能优化设计中已得到广泛的应用，其基本原理及优化过程见参考文献[7]。

2.2.4 优化设计结果及其分析

以船模（缩比1:15）在Fn=0.203时的总阻力最小作为优化目标对其线型进行优化设计。PSO算法的种群粒子数为36个，共迭代10次。船模阻力数值计算在并行计算机上进行（共使用八个节点），完成整个优化设计共用时约180个小时。优化方案与设计方案模型阻力结果比较如表3和图9所示，船体外形与线型比较如图10所示。

从表3可知，优化方案在航速12 kns时的模型总阻力减小了7.7%，剩余阻力系数减小了26.6%；排水量和湿表面面积略有减小，分别为0.37%和0.19%。表中还给出了其他航速时的阻力结果对比，可以看出在12 kns和14 kns附近总阻力的收益十分显著。

图9 最优方案与改型设计方案模型总阻力比较Fig.9 Comparison of the total resistance between the optimized and the redesign case at different speeds

图10 最优方案与改型设计方案线型比较Fig.10 Comparison of bodyplan between the optimized and the redesign hullform

图11 优化方案与改型设计方案自由面兴波波幅比较Fig.11 Comparison of wave contours between the optimized and the redesign case

表3 优化方案和改型设计方案模型阻力数值计算结果比较（模型缩比1：15）Tab.3 Comparison of resistance components between the optimized and the redesign case(λ=1:15)

图11给出了优化方案和设计方案自由面兴波波幅云图比较，从图中可以看出优化方案的自由面兴波波幅较设计方案明显减小。

3 结 论

本文介绍了“探索一号”科考船船体改型设计，采用CFD数值方法对其阻力性能进行了计算分析；之后，基于SBD数值仿真设计方法，以航速12 kns时的总阻力作为优化目标，采用PSO优化算法对其线型进行了优化设计。结果表明：在满足工程约束条件下，最优方案总阻力收益十分显著，航速12kns时模型总阻力减小了7.7%，换算到实船总阻力减小了11.6%。SBD船型设计方法的应用为“探索一号”科考船快速性能提升提供了有力的技术支撑。

[1]Campana E F,Peri D,Tahara Y,Kandasamy M,Stern F.Numerical optimization methods for ship hydrodynamic design[C].SNAME Annual Meeting,2009.

[2]Campana,E F,Liuzzi G,Lucidi S,Peri D,Piccialli V,Pinto A.New global optimization methods for ship design problems[J].Optimization Engineering,2009,10:533-555.

[3]Hyunyul Kim,Chi Yang,Heejung Kim,Ho Hwan Chun.A combined local and global hull form modification approach for hydrodynamic optimization[C]//28th Symposium on Naval Hydrodynamics.Pasadena,California,2010:12-17.

[4]赵 峰,李胜忠,杨 磊,刘 卉.基于CFD的船型优化设计研究进展综述[J].船舶力学,2010,14(7):812-821.Zhao Feng,Li Shengzhong,Yang Lei,Liu Hui.An overview on the design optimization of ship hull based on CFD techniques[J].Journal of Ship Mechanics,2010,14(7):812-821.

[5]李胜忠,倪其军,赵 峰,刘 卉.大方形系数低速船艉部线型多目标优化设计[J].中国造船,2013,54(3):1-10.Li Shengzhong,Ni Qijun,Zhao Feng,Liu Hui.Multi-objective design optimization of stern lines for full-formed ship[J].Shipbuilding of China,2013,54(3):1-10.

[6]Li Shengzhong,Zhao Feng,Ni Qijun.Bow and stern shape integrated optimization for a full ship by sbd technique[J].Journal of Ship Research,2014,58(2):83-96.

[7]李胜忠.基于SBD技术的船舶水动力构型优化设计研究[D].无锡:中国船舶科学研究中心,2012.Li Shengzhong.Hydrodynamic optimization for ship hull form design based on SBD techniques[D].Wuxi:China Ship Scientific Research Center,2012.

[8]Li Shengzhong,Zhao Feng,Ni Qijun.Multi-objective optimization for ship hull form design using sbd technique[J].Computer Modeling in Engineering&Sciences,2013,92(2):123-149.

[9]李胜忠,蒋昌师,倪其军,赵 峰.基于FFD重构方法的船型优化设计及其模型试验验证[C].第二十六届全国水动力学研讨会暨第十二届全国水动力学学术会议,2014.Li Shengzhong,Jiang Changshi,Ni Qijun,Zhao Feng.Hull-form design optimization based on Free-form Deformation and experimental verification[C].Proceedings of the 26th National Conference on Hydrodynamics&13th National Congress on Hydrodynamics,2014.

[10]赵 峰,李胜忠,杨 磊.全局流场优化驱动的船舶水动力构型设计新方法[J].水动力学研究与进展A辑,2017,32(4):395-407.Zhao Feng,Li Shengzhong,Yang Lei.The ship hydrodynamic configurations design driven by a global flow optimization[J].Journal of Hydrodynamics,2017,32(4):395-407.