复杂地形下平台水弹性响应研究

倪歆韵，田 超，程小明，杨 鹏，吴 波

（中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

传统上计算浮体的运动响应多采用有限均匀水深或无限水深方法，这对深海区域或地形变化不大的海域，计算结果已经能满足工程应用的需求。但随着岛礁建设开发的需求，需要在近岛礁区域布置大型浮体，沿浮体水平尺度范围内地形是变化的，已经不能用均匀水深来表示，地形的变化影响波浪的传播，从而影响浮体在波浪下的响应。因此，在研究近岛礁浮体的水动力响应时需要考虑地形变化对水动力性能的影响。但是，现有研究成果显示，针对这方面的研究较少，在大尺度范围内考虑地形变化还比较困难。宋皓[1]为研究由于海底变化所造成的非均匀环境，在上海交通大学海洋工程国家重点实验室进行了试验，通过在底部分别放置两个不同弦长的圆柱形沙丘和一个三维的椭圆形沙丘来模拟不平坦的底部，研究表明底部不平坦引起的非均匀环境确实对超大型浮体的水弹性响应有一定的影响，同时在论文中还分别给出了多重尺度法和三维实体模型处理这一问题的理论方法。Buchner[2]使用1:20的人工斜坡底来模拟海底，进行了试验和计算研究，水深从35 m变到8 m，斜坡水平长度550 m。相比均匀水深，带斜坡情况下船体运动具有根本的不同。Ferreira[3]基于Buchner的研究工作，比较了不同斜坡形状的绕射效应。斜坡侧面和后部的突变会产生折射和反射效应。研究结果显示，当斜坡水平尺度够长，侧面截面没有突变时，船体的水动力系数和运动响应随频率波动较小，与等水深结果较接近，但在低频区会有些振荡。

本文为研究岛礁附近区域地形变化对浮体性能的影响，基于三维水弹性和有限水深格林函数，开展浮体在复杂地形下的水弹性响应。先从简单浮体与地形组合入手，验证计算方法和程序的准确性，再以某一实际浮体为计算对象，分析该浮体在实际复杂地形下的响应，并与等水深结果进行比较，得到地形对浮体响应影响的一些规律和趋势。

1 三维水弹性理论

1.1 速度势分解

三维线性水弹性力学理论[4]与三维非线性水弹性力学理论[5-6]可用于分析超大型浮式结构物在非均匀海底与波浪环境中的结构动响应，浮体结构的总变形可以分解为若干主模态的线性叠加，结构弹性变形诱导的辐射势可以表示为 φr（x，y，z，）t，下标r对应于结构的某一变形主模态，总的速度势可以表示为：

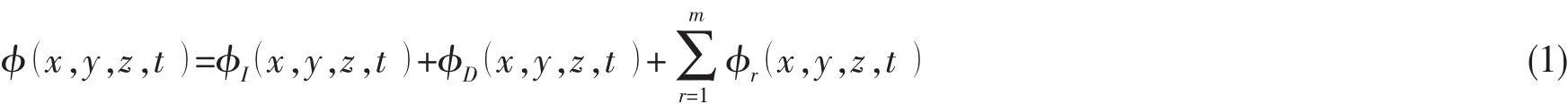
其中：φI（x，y，z，t ）为波浪入射势，φD（x，y，z， t）为波浪绕射势，m为自由浮体的主模态数，其中前六阶为刚体运动。

在微幅入射波和微幅运动假设前提下，各速度势可以使用分离变量法将位置坐标和时间分离开，可以表示为：

所有模态线性叠加后，浮体任一点的位置矢量可以表示为：

其中：pr（t）为r阶模态的主坐标响应｝为各阶广义位移；v0，w0，α0，β0，γ0｝为广义刚体位移；r=1…6 表示前 6 个自由度的刚体运动，分别对应纵荡、横荡、垂荡、横摇、纵摇和艏摇。

1.2 线性水弹性力学运动方程

假定浮体结构周围为理想、不可压缩流体，波浪幅值为小量，可得到浮体的线性水弹性力学运动方程为[4]：

2 复杂海底环境影响

本文采用有限水深格林函数求解辐射势和绕射势。有限水深脉动源格林函数的积分形式可以表示为[4]：

其级数形式[4]：

当海底为复杂海底形状，水深不均匀时，在平均湿表面和海底分布有限水深脉动格林函数源强，此时除了要满足物面边界条件外，还要满足海底不可穿透条件，即：

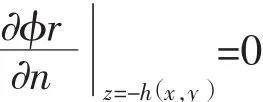
流域内各点速度势为[7]：

其中：S0为物面，SB为海底，σ（）Q为物面和海底上的源强。

3 计算方法准确性测试

3.1 计算对象

图1 多体耦合模型Fig.1 Coupling model of two bodies

将长方形浮箱与梯形结构物进行组合计算。长方体浮箱长20 m，宽5 m，吃水2 m，梯形结构物为等腰梯形，梯形上表面长10 m，下表面长30 m，高2 m，宽度20 m，模型整体前后左右均对称[8]。此模型的建立用梯形物体模拟海底地形，浮箱模拟自由液面或水中的结构物，目的是测试在海底地形影响下，浮式结构物的水动力响应计算结果的准确性。梯形底部开口，底部距自由液面为10 m，计算水深设为10.2 m，力、力矩参考点设在自由液面浮箱的中心位置。

3.2 结果比较

图2给出了浮箱的水动力系数、波浪激励力与商业软件AQWA的比较结果，两者吻合一致，从而证明了本文计算方法的准确性。（注：THATFS为中国船舶科学研究中心开发的三维水弹性软件）。

图2 浮箱水动力系数及波浪激励力计算结果比较Fig.2 Hydrodynamic coefficients and exciting forces of buoyancy tank

4 复杂地形下某浮式平台的水弹性计算

本文选定某浮式平台开展带地形计算，平台外形类似于一个方盒子，长为100 m，宽25 m，高6 m，吃水2.5 m，主尺度参数见表1。

图3 平台结构有限元模型和水动力网格Fig.3 Finite elements model and hydrodynamic meshes of a platform

表1 平台主要参数Tab.1 Main parameters of platform

4.1 平台带地形整体计算模型

图4为浮式平台带地形三维视图，本文中先假设地形左右对称，前后不对称。定义地形深水区域为前部区域，靠岸边区域为后部区域。视线从前部区域向后部区域观看，视线的左手边定义为左侧，右手边定义为右侧。图中用箭头指明了平台和地形各自所对应的网格部分。

地形范围为长250 m，宽180 m。平台中心距地形前后两端的水平距离均为125 m，距左右两侧的水平距离为90 m，布放在地形区域的正中心位置。地形以外的部分采用均匀水深，取26.2 m。

图4 浮式平台带地形三维视图Fig.4 3D views of a platform with landform

4.2 模态分析结果

本文给出了此平台有限元模型前4阶弹性模态的分析结果，每阶模态对应的固有频率见表2，表2同时给出了平台与波浪在这4阶弹性模态的共振频率。弹性模态变形如图5所示（比例因子为2 000）。

表2 平台弹性模态结果Tab.2 Results of modal analysis for a platform

图5前四阶弹性模态分析结果Fig.5 Results of modal analysis for first four modes

4.3 水弹性响应计算结果

图6 ～8给出了0°、45°和90°浪向下浮体在复杂地形下的水弹性响应结果。因为复杂地形的平均水深大约为10 m，所以同时计算了等水深10 m的浮体水弹性响应结果，并将带地形结果与等水深结果进行了比较。图中实线是带地形结果，虚线是等水深结果。

图6 主坐标响应计算结果（0°浪向）Fig.6 Responses of principle coordinates(0°wave direction)

4.4 波浪载荷

通过第7、9阶弹性模态响应可以计算得到浮体横剖面的载荷，图9给出了复杂地形下平台中剖面的垂向弯矩传递函数。

5 结果分析

由浮体水弹性计算结果可以看出：

图9 垂向弯矩传递函数Fig.9 Transfer functions of vertical moment

（1）因为该浮式平台布放处平均水深约在10 m，所以本文将带地形计算结果与有限水深10 m的计算结果进行了比较。计算给出了浮体9个模态（包括6个刚体模态，3个弹性模态）的主坐标响应，45°和90°浪向时仅给到第7阶模态，因为从0°结果可以看出，相比第7阶模态，第8、9阶模态对浮体弹性变形的贡献很小。通过带地形和有限水深在浪向角0°、45°和90°下的水弹性响应结果的比较发现，两者在数值量级和总体变化趋势基本一致，弹性模态在波浪频率共振点也基本一致，从而有效地说明了带地形计算结果的合理性。

（2）虽然带地形计算结果和有限水深计算结果趋势一致，但是在低频区，带地形情况下平台的主坐标响应波动较大，相比而言，有限水深在此频率区域主坐标响应较光滑。

（3）由于地形从深水到浅水是有水深变化的，前后不是对称的，所以在0°浪向时，第2、4、6、8模态即反对称模态的主坐标响应不为0，地形的变化对反对称模态响应产生了影响，有限水深情况下，由于地形是对称的，所以此时反对称模态的响应为0。在90°浪向时，由于地形左右的对称性，所以地形对平台的纵荡、纵摇、艏摇与有限水深的计算结果完全一致，在这3个模态的主坐标响应为0。

（4）第7阶模态在每个浪向角时都出现了和波浪频率共振的峰值，而第8、9阶模态未能在对应的预估共振点处出现峰值，这主要是因为此平台长度较小，弹性变形不是太明显，第7阶模态为弹性变形的主要贡献量。0°浪向时，第7阶模态对第9阶模态产生了一定的耦合影响，如图6所示，P9在5.3 rad/s左右时产生了一个较微小的峰值，与第7阶模态的波浪共振点相对应。

（5）图6-8的结果显示，地形对弹性模态高频共振点处的响应具有一定的抑制作用，而在低频区，地形的存在会增大平台的运动响应。

6 结 语

本文采用有限水深格林函数程序近似模拟水质点的运动，将地形考虑成一个物体，在地形网格节点上布源，从而加入地形对平台的影响，简化地形对入射波浪场的影响，采用有限水深均匀入射波条件，在此条件下计算地形对平台波浪绕射的影响。平台所布放处的水深约在10 m左右，所以将带地形结果与有限水深10 m结果进行了比较，两者在整体趋势上基本一致，在低频区带地形情况下平台的主坐标响应波动较大。由于平台长仅100 m，仅第7阶弹性模态主坐标响应占据了主要作用，更高阶弹性模态的对平台响应的贡献相对较小。

[1]宋 皓.超大型浮体在非均匀海洋环境下的水弹性响应研究[D].上海:上海交通大学,2004.Song Hao.Hydroelastic response analyses of very large floating structures under inhomogeneous sea environment[D].Ph.D thesis.Shanghai:Shanghai Jiao Tong University,2004.

[2]Ferreira M D,Newman J N.Diffraction effects and ship motions on an artificial seabed C]//24th IWWWFB.Zelenogorsk.Russia,2009.

[3]Buchner,Bas.The motions of a ship on a sloped seabed[C].Pro.25th OMAE,2006(OMAE2006-92321).

[4]Wu Yousheng.Hydroelasticity of floating bodies[D].Ph.D thesis.Brunel:Brunel University,1984.

[5]Wu Yousheng,Hisaaki Maeda,Takeshi Kinoshita.The second order hydrodynamic actions on a flexiblebody[J].Seisan-Kenkyu of Institute of Industrial Science of Univ.of Tokyo,1997,49(4):8-13,14-19.

[6]Tian Chao,Wu Yousheng.The non-linear hydroelastic responses of a ship traveling in waves,hydroelasticity in marine technology,Wu and Cui(eds)[M].Beijing:National Defense Industry Press,2006:14-24.

[7]刘应中,缪国平.船舶在波浪上的运动理论[M].上海:上海交通大学出版社,1987.Liu Yingzhong,Miao Guoping.Motion theory of ship in waves[M].Shanghai:Shanghai Jiao Tong University,1987.

[8]倪歆韵,田 超.有限水深地形模拟测试报告[R].无锡:中国船舶科学研究中心科技报告,2014.Ni Xinyun,Tian Chao.The test report for the hydrodynamics of structure with the effect of seabed in finite water depth[R].Wuxi:China Ship Scientific Research Center,2014.