空化模型在低温流体空化流动三维计算中的应用与评价

孙铁志，魏英杰，王 聪，路中磊

（1.大连理工大学 船舶工程学院，辽宁 大连 116024；2.哈尔滨工业大学 航天学院，哈尔滨 150001）

0 引 言

当流场中液体的压强降到当地温度下的饱和蒸汽压强以下时，将会发生空化现象[1]。空化多存在于涡轮泵、螺旋桨等流体机械中，空化的发生会导致机械振动、噪声以及机械性能下降等影响，所以空化问题引起了国内外学者开展相关研究。低温流体例如液氢、液氧等介质的空化常存在于液体火箭发动机推进系统中，由于低温流体空化过程中热力学效应的影响以及低温环境条件等因素的限制，增加了开展相关研究的难度，但国内外学者一直致力于这方面问题的研究。

Stahl和Stepanoff[2]最早提出了B因子理论，分析了热力学效应对泵的扬程的影响；后来Sarosdy和Acosta[3]开展了水和氟利昂空化的对比试验，发现了氟利昂液体空化时空泡呈泡雾状；二十世纪七十年代Hord[4-5]在NASA的资助下，系统地开展了液氮的低温空化试验，从而加深了对低温流体空化特性的直观认识。随着计算机技术的发展，近些年通过数值计算也开展了低温流体空化特性的研究，Hosangadi等人[6]采用Merkle空化模型对液氢和液氮流体空化流动进行了计算，指出了热力学效应对空化特性具有显著影响；Tseng等人[7]对质量传输模型的参数进行了敏感性分析。国内的马相孚、张小斌和黄彪等人[8-10]对低温流体空化流动问题开展了二维数值模拟研究，初步建立了二维数值计算方法。

本文在计算过程中通过CFX Expression Language语言将不同空化模型嵌入到CFX软件中，并将液氮、液氢的密度、比热容、热传导系数以及饱和蒸汽压强等随温度变化的物性参数引入到求解代码中，各个参数随着温度的改变实时更新；同时考虑空化过程汽化潜热的影响，并将其以源相的形式添加到能量方程中，从而形成了一套计算低温流体空化的三维数值方法。

通过将数值计算结果与试验数据进行对比和分析，评价不同空化模型的有效性，为今后深入准确全面地预测低温流体空化特性奠定基础。

1 数值计算方法

1.1 基本控制方程

对于考虑热力学效应的低温液体空化流动问题计算的控制方程，除了连续性方程和动量方程外，还包括包含能量源项的能量方程，依次如下：

其中：ρm=αlρl+αvρv为混合相的密度；下标v和l分别代表汽相和液相；下标i和j代表坐标方向；u为速度；μ为流体的动力粘度，μt是湍流粘度；Keff为热传导系数，L为汽化潜热。

1.2 湍流模型

选取的SST（Shear Stress Transport）湍流模型通过在BSL（Baseline k-ω）湍流模型添加涡粘度限制方程后可有效预测流动分离问题，其中BSL模型方程如下：

其中：μ为流体的动力粘度；μt为湍流粘度；Pkb表示浮力引起的湍动能的产生项；Pk表示由于粘性力引起的湍动能的产生项；常数 β′=0.09、α1=5/9；F1和F2为混合函数；S为应变率的不变测度。

1.3 空化模型

在物理上空化过程是由热力学和动力学约束的相变过程，通过建立液—汽两相之间质量传输的蒸发源相（）和凝结源相（）的方程来表示两相之间的转换过程，通过求解传输方程以获得体积分数（αl）或质量分数（fv）的分布，两种形式方程如下：

SST模型中添加的涡粘度限制方程形式为：

目前空化模型的建立主要是基于Rayleigh-Plesset汽（气）泡动力学方程（9）的推导，得到描述汽（气）泡生长和溃灭的基本方程。

式中：pv为泡内压强，p为气泡周围压强，R为汽泡半径，ρl为液体密度，T为液体表面张力。

本文计算采用的空化模型是近些年提出并在常温流体空化计算中具有广泛应用的模型，如表1所示。其中Kubota模型可有效解释涡流和空化气泡之间粘性效应的相互作用，并重点考虑了空化发生时初生和生长过程空泡体积变化的影响，对于非定常空化流动具有较强适用性；Merkle模型的推导建立过程是用大气泡群代替单个气泡，蒸发源相和凝结源相表达式直接与压力差相关，这区别于Kubota模型压力差的平方根；Kunz模型在蒸发和凝结过程中起主导因素的分别是压力差和体积分数。而Kunz模型中的质量传递建立是基于两种不同策略，从液相到汽相的转换主要取决于空化区域压力低于饱和蒸汽压力的差值，而从汽相到液相转换时，质量传输是体积分数的三阶多项式，所以体积分数的改变对Kunz模型中影响显著[11-13]。

表1 不同空化模型方程蒸发源相与凝结源相表达式Tab.1 Evaporation and condensation source term expression of different cavitation models

其中：Cdest和Cprod为蒸发系数和凝结系数的经验常数；αug为非凝结气体的体积分数；U∞为无穷远处流场速度；t∞为特征时间。

2 计算结果与分析

Hord在二十世纪七十年代系统地开展了低温条件下液氢和液氮空化流动的试验研究，其获得的试验数据被国内外学者广泛地用于数值计算结果的验证。本文基于Hord试验，开展了液氮绕水翼空化流动和尖顶拱在液氢中空化流动的三维计算研究，通过与试验数据对比，综合了评价Kubota，Kunz以及Merkle三种空化模型在不同低温介质、不同几何模型条件下空化流动计算中的适用性。

2.1 液氮绕水翼空化流动计算结果与分析

2.1.1 计算模型和网格划分

液氮绕水翼空化计算模型与Hord试验一致，试件结构及尺寸如图1所示，根据试验条件，计算域入口采用速度入口，出口为压力开口，流域边界及水翼设置为绝热不可滑移壁面，并在翼型表面分别设置五个温度监测点和五个压力监测点，以便将数值计算结果与试验数据进行对比。图2给出了计算模型网格划分，计算域内采用H-型和C-型网格，同时在水翼附近网格进行加密处理，以提高计算效率，有效捕捉翼型周围流场参数，且在计算过程中对网格无关性进行了验证。

图1 计算模型结构Fig.1 Structure of computational model

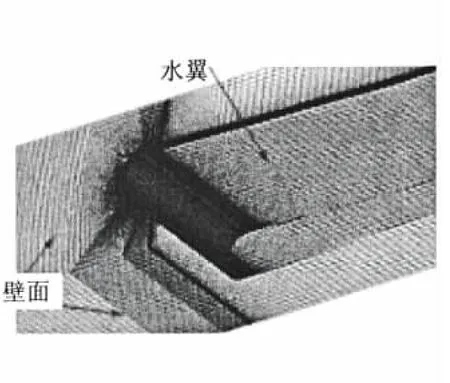
图2 计算域模型网格划分Fig.2 Grids of computational model

为有效评价不同空化模型的适用性，根据试验数据随机选取三种不同工况，如表2所示。计算过程中保持计算网格、湍流模型、边界条件以及试验参数等条件一致。通过对比不同空化模型下空化区域两相分布特性、翼型周围压力和温度数据等综合因素，对三种不同空化模型的适用性进行评价。

表2 计算工况（液氮）Tab.2 Computational cases(Liqiud nitrogen)

2.1.2 空化区域相分布特性

为分析不同空化模型下液氮绕水翼空化流场两相分布特性，首先给出290C工况三种模型的空化特性对比，如图1所示。从图1（a）中三维空泡形态的对比可以看出，空化发生起于翼型头部，并沿翼型向下游发展，发展过程中空泡厚度增加，且在空泡闭合位置出现回射流。从图中也可以看出不同空化模型下空化特性的差异：Kubota空化模型计算得到的空泡厚度最大，并且最大厚度位置接近空泡尾部；Merkle模型计算的空泡形态类似于椭球形，整体汽—液交界面轮廓过渡圆滑；而Kunz模型计算的空泡在尾部闭合区域表现尖锐，回射现象更加明显，并且空泡厚度最小。同时Kubota模型计算得到的空泡长度为23.0 mm，Merkle模型为23.6 mm，Kunz模型为27.4 mm，试验值为22.96 mm。虽然三种模型计算的结果都与试验值接近，但Kubota模型计算的空泡长度与试验结果吻合最好。

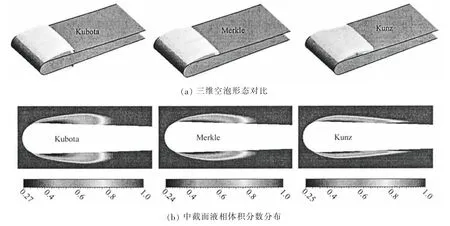
图3 290C工况空化区域相分布特性对比Fig.3 Phase distribution of 290C case at the cavitation region

2.1.3 温度场和压力场分布对比

为进一步对比三种空化模型计算结果的差异和验证数值计算结果的准确性，图4给出了三种空化模型在不同工况下数值计算结果与Hord试验数据的对比，计算结果与试验数据具有较好的一致性，从而验证了计算方法的有效性。对比不同空化模型的计算结果可以看出，不同工况下同一空化模型计算的压力和温度整体变化趋势一致，在空化区域压力和温度值降低，且压力和温度值并不保持恒定，这主要是由于液氮等低温液体空化时由于热力学效应会引起空化区域温度降低，而液氮饱和蒸汽压强是温度的函数，且随温度变化敏感，从而导致空化区域压强值呈梯度变化，这一特性与常温水有明显区别。三种空化模型计算的空化区域的最大压降、最大温降有差异，且在空化区域压力和温度曲线变化的梯度不同。压力方面：在空化区域Kubota模型计算得到的最大压降（①位置）最大，在空化区域压力值相对稳定，恢复到无穷远处值压力曲线起点（②位置）滞后，且变化梯度最大，Kubota模型计算的空泡闭合区域（③位置）会有压力峰值；Kunz模型计算的压力曲线梯度总体最小，Merkle模型计算的压力梯度值介于两者之间；温度方面：总体而言Kubota空化模型计算得到的温度曲线变化梯度最大，空化区域最大温降值较大，Kunz模型得到的温度曲线变化最缓慢，且最大温降最小。综合对比可以看出Kubota模型对液氮绕水翼空化流动预测较好，Merkle模型可较好地反映出空化区域温度场分布。

图4 三种空化模型下压力和温度计算结果与试验对比Fig.4 Comparison of the numerical results with experimental data by three cavitation models

2.2 液氢空化流动计算结果与分析

液氢空化计算模型与Hord[5]试验一致，如图5所示。计算几何模型为尖顶拱形回转体，且在尾部扩张，计算域上游为圆柱形回转体，并在尖顶拱肩部位置开始扩张，如图5（a）所示。计算模型具体尺寸如图5（b）所示，其中尖形拱直径为9.1 mm，肩部倒角半径为2.3 mm。计算模型网格划分方法与2.1节中水翼模型一致，在尖形拱头部空化区域网格精细划分以有效捕获空化流动特性。

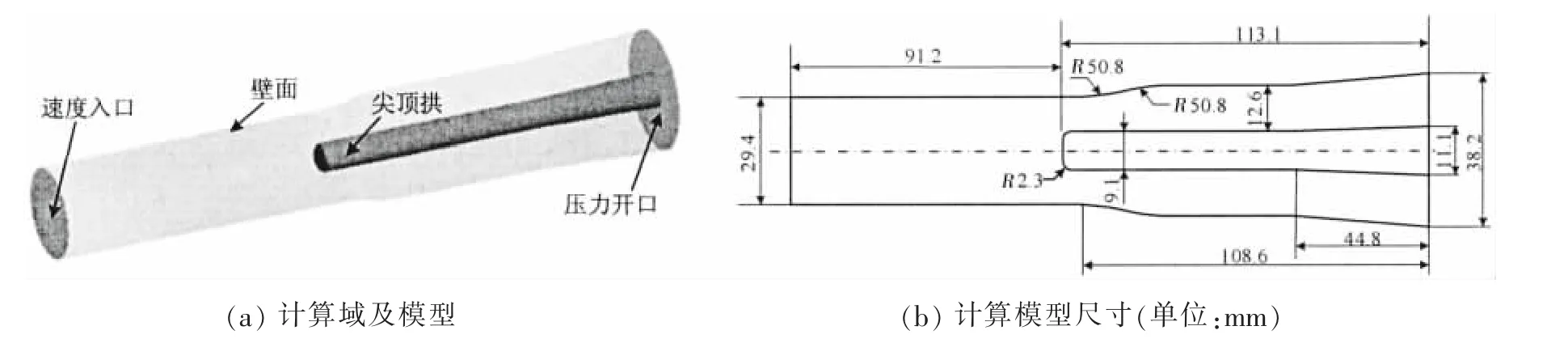
图5 液氢空化计算模型Fig.5 Computational model of cavitating flow in liquid hydrogen

同样，根据Hord试验随机选取三种试验工况作为计算对比验证，如表3所示。计算边界条件与

2.1 节中液氮绕水翼空化设置一致，尖形拱和水洞边界都设置为绝热壁面。

图6给出了三种空化模型下尖顶拱在液氢中空化流动数值计算结果，沿尖顶拱周围沿轴向方向分布的压力和温度变化趋势与2.1节中液氮绕水翼空化结果整体变化趋势一致，数值计算结果与试验数据吻合较好。从图6（a）中可以看出，三种空化模型计算的347B和366B工况压力结果差异不明显，在513B工况中Kubota模型计算的压力结果与试验数据最接近，其次是Merkle模型。从图6（b）给出的三种空化模型计算得到的温度变化与试验对比可以看出，Kubota空化模型计算得到的最大温降值最高，Kubota和Merkle两种空化模型对温度场的预测要优于Kunz空化模型。综合对比可以看出Kubota和Merkle模型对尖顶拱在液氢中空化流动的温度变化预测较准确，Kubota模型可较好地计算出尖顶拱周围压力场分布。

表3 计算工况（液氢）Tab.3 Computational cases(Liqiud hyrogen)

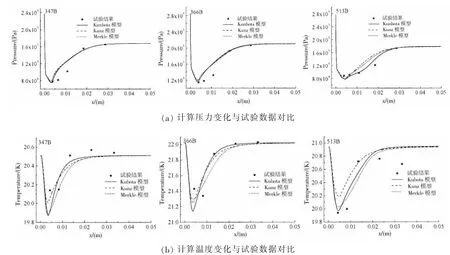
图6 液氢中三种空化模型计算的压力和温度结果与试验数据对比Fig.6 Computed pressure and temperature profiles in liquid hydrogen compared with experimental data

2.3 不同空化模型机理分析与评价

为说明不同空化模型得到的空化特性、压力分布和温度降低的差别，以290C（液氮）和366B（液氢）工况为例，从两种流体介质不同空化模型下空化区域蒸发源相和凝结源相分布特性进行分析，如图7所示。从图中蒸发源相分布对比可以看出，两种介质中分布趋势一致，其中Kubota模型的值最小，Merkle模型和Kunz模型计算的结果整体接近；从表1中不同空化模型源相公式可知，蒸发源相值主要取决于液相体积分数αl和pv-p的大小，Kubota空化模型中蒸发源相是pv-p的二分之一次方，所以Kubota模型需要较大的压降以驱动相同的空化强度。

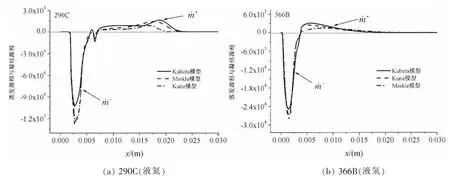
图7 三种空化模型下蒸发源相和凝结源相对比Fig.7 Comparison of the evaporation and condensation source term by three cavitation models

3 结 论

为评价Kubota、Merkle和Kunz三种空化模型对低温流体空化过程流场特性预测的适用性，通过对CFX软件的二次开发，将空化模型、能量源相和液氮、液氢物性参数嵌入到CFX求解代码中，建立了考虑热力学效应下液氮绕水翼空化流动和尖顶拱在液氢中空化流动三维数值的计算方法，通过将计算结果与试验数据对比分析，得到主要结论如下：

（1）不同空化模型计算得到的空化区域空化特性差异明显，Kubota模型计算的空泡厚度最大、液相体积分数沿径向变化缓慢，Merkle模型次之；Kunz模型计算的空泡长度最大，空化闭合区域回射流现象明显。

（2）空化模型质量传输机制显著影响着空化区域流场特性，空化区域压差、液/汽相体积分数值以及流体介质密度是决定着空化模型方程中蒸发源相和凝结源相质量传输大小的主要因素，进而影响着空化流场特性，从而导致Kubota模型计算的空化区域压降较大，空泡闭合位置压力变化梯度最大，温度变化迅速；而Kunz模型在空化区域从低压恢复到无穷远处压强缓慢。

（3）三种空化模型对低温流体空化流动流场结果预测存在差异，Kubota空化模型可有效计算流场压力分布，Merkle模型可较好地反映热力学效应下空化区域温度降，而Kunz模型计算的压力、温度结果与试验数据偏差最大，总体上Kubota模型和Merkle模型适用性较强。

[1]Joseph D D.Cavitation in a flowing liquid[J].Physical Review E,1995,51(3):R1649.

[2]Stahl H A,Stepanoff A J.Thermodynamic aspects of cavitation in centrifugal pumps[J].Trans.ASME,1956,78(8):1691-1693.

[3]Sarosdy L R,Acosta A J.Note on observations of cavitation in different fluids[J].Journal of Basic Engineering,1961,83:399-400.

[4]Hord J.Cavitation in liquid cryogens II-Hydrofoil,1973[R].NASA CR-2156.

[5]Hord J.Cavitation in liquid cryogens III-Ogives,1973[R].NASA CR-2242.

[6]Hosangadi A,Ahuja V.Numerical study of cavitation in cryogenic fluids[J].Journal of Fluids Engineering,2005,127(2):267-281.

[7]Tseng C C,Shyy W.Modeling for isothermal and cryogenic cavitation[J].International Journal of Heat and Mass Transfer,2010,53(1):513-525.

[8]Ma Xiangfu,Wei Yingjie,Wang Cong,et al.Simulation of liquid nitrogen around hydrofoil cavitation flow[J].Journal of Ship Mechanics,2012(12):1345-1352.

[9]Zhang X B,Wu Z,Xiang S J,et al.Modeling cavitation flow of cryogenic fluids with thermodynamic phase-change theory[J].Chinese Science Bulletin,2013,58(4-5):567-574.

[10]Huang B,Wu Q,Wang G.Numerical investigation of cavitating flow in liquid hydrogen[J].International Journal of Hydrogen Energy,2014,39(4):1698-1709.

[11]Kubota A,Kato H,Yamaguchi H,et al.Unsteady structure measurement of cloud cavitation on a foil section using conditional sampling technique[J].Journal of Fluids Engineering,1989,111(2):204-210.

[12]Merkle C L,Feng J,Buelow P E O.Computational modeling of dynamics of sheet cavitation[C]//Proceedings of the 3rd International Symposium on Cavitation.Grenoble,France,1998.

[13]Kunz R F,Boger D A,Stinebring D R,et al.A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction[J].Computers&Fluids,2000,29(8):849-875.