基于ABAQUS的栅格翼展开试验动力学分析

冉振华，曾杜娟，黎汉华，邵业涛



基于ABAQUS的栅格翼展开试验动力学分析

冉振华，曾杜娟，黎汉华，邵业涛

（北京宇航系统工程研究所，北京，100076）

通过对栅格翼地面展开试验运动过程进行理论分析，并结合有限元分析方法分析了栅格翼展开过程中结构强度和增大铰链力矩对展开时间及结构强度的影响。结果表明，栅格翼展开至限位时，栅格翼与壳段接触点和栅格翼根部栅格位置应力远大于静强度分析结果，增大栅格翼铰链力矩对栅格翼展开时间影响较小，但可明显降低栅格翼展开时刻角速度，减小限位后的冲击能量。

栅格翼；有限元；动力学分析

0 引 言

栅格翼作为一种新型气动控制舵面，可折叠安装在飞行器上，不增大其外形尺寸，飞行中在气动力作用下自动打开，有利于箭体的存放、运输和发射，具有弦向压心变化小，失速舵偏角大，可以在较宽马赫数数范围内调整升力线斜率等诸多优点[1~6]，在国外导弹武器及运载火箭中均有应用，中国CZ-2F运载火箭逃逸系统选用栅格翼提供气动控制力。

栅格翼由外部框架和内部众多的薄格壁布置成框架形式或蜂窝形式，对加工工艺要求高，其结构强度、稳定性分析、飞行中响应时间对姿控影响、打开过程对结构的冲击等问题需要进一步研究。

本文通过对栅格翼地面展开试验运动过程理论分析，并结合有限元分析方法分析了栅格翼展开过程中结构强度和增大铰链力矩对展开时间及栅格翼强度的影响。

1 试验方案

栅格翼展开试验系统见图1，包括箭体模拟件、栅格翼、铰链、分离弹簧、配重等。试验中，分离弹簧和重物同时解锁，栅格翼在分离弹簧作用下展开，随着重力力矩逐渐增大，栅格翼与弹体贴合状态（0°）转换为打开状态（90°）并限位。展开过程中，当栅格翼旋转角度达到15°时，铰链开始产生阻尼力矩，随着展开角度的增大，阻尼力距也越来越大，90°时达到最大。

图1 栅格翼展开试验示意

栅格翼、壳段材料为ZL205A，铰链及转轴材料为45钢，配重模拟气动力矩，根据风洞吹风结果，按350 ~540 kg逐级加载，承力点距旋转铰链650 mm。

2 栅格翼展开过程动力学分析

分别对重物和栅格翼进行受力分析[7]，试验过程栅格翼打开过程动力学方程组如下：

整理为关于打开角度的二阶非线性微分方程：

对式（2）进行求解，可求得栅格翼打开角度及角速度随时间的变化情况分别如图2~ 4所示，挂载不同重物时打开时间与栅格翼展开时刻角速度见表1。

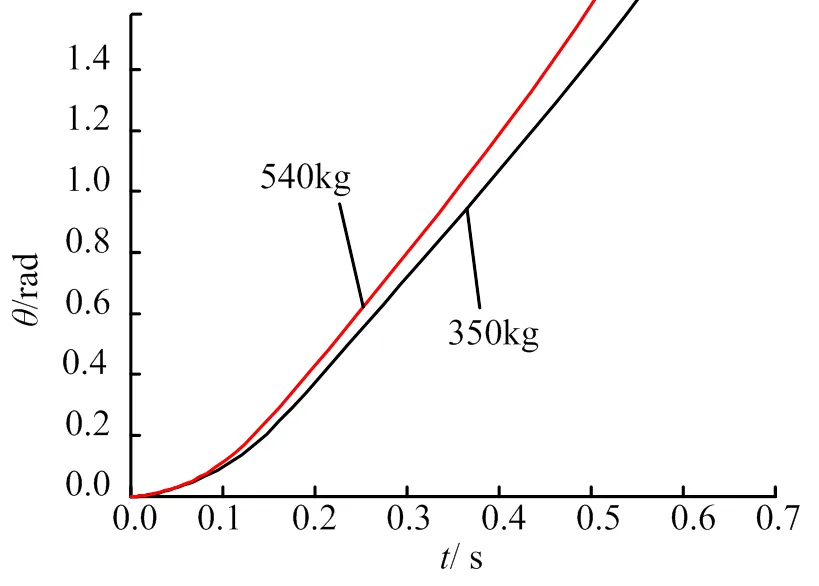
图2 栅格翼角度随时间变化情况

图3 栅格翼角速度随时间变化情况

图4 栅格翼角速度随角度变化情况

表1 栅格翼打开时间与展开时刻角速度

3 试验过程有限元分析

3.1 有限元分析模型

本文采用ABAQUS6.11，考虑材料的非线性及几何非线性，对试验工况进行隐式结构动力学分析[8]，分析中采用N-mm-s单位制，对壳段及栅格翼结构进行整体建模，模型中各部分结构均采用六面体实体单元模拟，单元类型C3D8I，网格数量80万，对铰链及接触位置网格适当加密。采用面面接触算法来模拟连接螺栓与基座及栅格翼与基座的连接关系。有限元模型见图5、图6。

图5 整体有限元模型

图6 栅格翼与壳段的连接

根据试验工况，在重物加载工装上施加集中力载荷=3 500 N，对栅格翼施加初始角速度，分离弹簧与铰链阻尼采用Hinge进行模拟，并考虑弹簧和铰链的非线性。对模型整体施加重力场，模型中壳段与工装四处连接位置设置固定边界条件。

3.2 有限元分析结果

图7为栅格翼打开情况示意，第1次打开至90°过程中，随展开角度增大，角速度逐渐增大，继续打开至与壳段发生碰撞后栅格翼小幅反弹，如此反复多次后停止。

图7 栅格翼打开情况示意

栅格翼第1次达到90°后0.095 s时栅格翼动能最小，该时刻栅格翼与壳段发生碰撞时两者的应力应变达到最大值，对应栅格翼、壳段应力分别如图8、图9所示，结果表明，栅格翼最大塑性应变出现于与壳段接触位置，除此之外栅格翼根部靠近转轴2个栅格上塑性应变最大，为贯穿性屈服，应变值已达到材料ZL205A发生断裂时塑性应变，远大于静强度分析中最大应力265 MPa的分析结果；壳段最大塑性应变出现于栅格翼与壳段接触位置，塑性应变值为5%。

图8 栅格翼Mises应力

图9 壳段Mises应力

4 铰链阻尼力矩对栅格翼打开过程影响分析

为解决试验中栅格翼和铰链破坏问题，在不改变栅格翼和壳段基础上，尽量通过调整铰链阻尼来实现栅格翼的安全打开，同时尽量减小对栅格翼打开时间的影响。

4.1 铰链阻尼力矩对运动情况影响

假定铰链阻尼初始作用点15°位置不变，增大铰链阻尼力矩（15°~90°区间内阻力力矩，随角度线性变化）对栅格翼打开时间及展开时刻角速度的影响，分别如图10、图11所示，增大铰链力矩各工况栅格翼打开时间及展开时刻角速度见表2。

分析结果表明，增大铰链力矩对栅格翼展开时间影响较小，但可明显降低栅格翼展开时刻角速度，铰链增大至力矩2 400 N·m展开试验中测得展开时间为0.6 s，角速度为3.02 rad/s，与本文计算结果基本吻合。

表2 栅格翼打开时间与展开时刻角速度

图10 栅格翼角度随时间变化情况

图11 栅格翼角速度随角度变化情况

4.2 阻尼力矩增大至2 400 N·m有限元仿真结果

栅格翼动能最小时栅格翼、壳段应力分别如图12、图13所示，结果表明，栅格翼最大塑性应变值为3%，壳段最大塑性应变值为1.3%，小于材料ZL205A发生断裂时塑性应变，主要结构最大塑性应变较原方案减小约25%~40%，可以满足试验要求。

图12 栅格翼Mises应力

图13 壳段Mises应力

5 结 论

本文通过建立栅格翼打开动力学方程，并结合有限元方法对栅格翼展开试验中展开过程及零件结构强度进行了隐式动力学仿真分析，分析结果表明：

a）栅格翼展开至限位时，栅格翼与壳段接触点和栅格翼根部栅格位置应力远大于静强度分析结果，参数选择不合理将导致结构在该位置发生塑性断裂，栅格翼试验中需要重点关注该位置的应力应变；

b）不改变主要结构的情况下，增大铰链阻尼力矩对栅格翼展开时间影响较小，但可以显著减小栅格翼撞击限位时的角速度；

c）有限元分析结果表明，适当增大铰链阻尼力矩可显著减小栅格翼展开限位后的冲击能量，减小栅格翼和壳段应力。

[1] Fournier E Y. Wind tunnel investigation of grid fin and conventional planar control surfaces[R]. AIAA2001-0256, 2001.

[2] Washington W D, Miller M S. Grid fins-a new concept for missile stability and control[R]. AIAA-93-0035, 1993.

[3] James D, Milton E, Vaugh Jr. Subsonic flow CFD investigation of canard-controlled missile with planar and grid fins[R]. AIAA2003-27, 2003.

[4] 黎汉华, 石玉红. 栅格翼国内外研究现状及发展趋势[J]. 导弹与航天运载技术, 2008(6): 27-30.

[5] 雷娟棉, 吴小胜, 吴甲生. 格栅尾翼(舵)外形参数对气动特性的影响[J].北京理工大学学报, 2007, 27(8): 675-679.

[6] 陈少松, 徐琴, 王福华. 格栅翼组合体的超音速气动特性研究[J]. 弹道学报, 2000, 12(2): 50-54.

[7] 程靳. 理论力学[M]. 北京: 高等教育出版社, 2009.

[8] 王虎; 顾克秋. 牵引火炮非线性有限元隐式动力学分析[J]. 南京理工大学学报, 2006, 30(4): 462-466.

Dynamic Analysis of Grid Wing Expansion Test Based on ABAQUS

Ran Zhen-hua, Zeng Du-juan, Li Han-hua, Shao Ye-tao

(Beijing Institute of Astronautical Systems Engineering, Beijing, 100076)

The influence of structural strength and hinge moment on the opening time and structural strength of lattice wing is analyzed by theoretical analysis and finite element analysis. The results show that the stress of the grid wing and shell is much greater than that of the static strength analysis. The increase of the hinge moment has little effect on the lattice wing opening time, but it can reduce the angular velocity of the grid and reduce the impact energy.

Grid wing; Finite element; Dynamic analysis

1004-7182(2017)06-0098-04

10.7654/j.issn.1004-7182.20170621

V421.6

A

2016-10-23；

2017-05-23

冉振华（1987-），男，工程师，主要研究方向为运载火箭动力系统总体设计