弹射动力装置结构强度可靠性研究

刘宝龙，潘 硕，申 鹏，吴新跃



弹射动力装置结构强度可靠性研究

刘宝龙，潘 硕，申 鹏，吴新跃

（北京航天发射技术研究所，北京，100076）

通过对大量试验数据的统计分析，建立了弹射动力装置燃气压力峰值和结构材料强度性能的概率分布模型，并分析了热-机械载荷的耦合性，基于应力-强度干涉理论建立了动力装置壳体结构强度的可靠性模型，开展了动力装置结构强度可靠性评估与优化分析。研究表明，弹射过程中动力装置弹射内压峰值与燃气热载荷不存在耦合关系，且内压峰值服从正态分布，置信度99%；原动力装置壳体存在“过安全”设计，基于结构强度可靠度指标优化后，可实现减重30%。

弹射动力装置；结构可靠性；概率分布

0 引 言

弹射动力装置（以下简称动力装置）是导弹武器冷发射技术中发射平台的关键设备之一，一般由点火系统、主装药、燃烧室等组成，其主要功能是：在接到弹射指令后点火，主装药在燃烧室内迅速燃烧，瞬间产生大量高温高压燃气，经喷管进入发射筒内，在发射筒内建立一定压力；导弹在燃气压力的作用下加速运动，并按预定速度弹射出筒[1~3]。在上述过程中，燃烧室壳体作为弹射动力装置的主承载结构，承受高温高压燃气作用，其结构强度的可靠性直接决定了动力装置整体的承载可靠性。

在传统的动力装置设计体系下，往往采用“过安全”设计来确保结构强度可靠性，而缺乏结构可靠性的量化评估，从而导致动力装置结构重量大、成本高，无法满足新形势下发射平台整体轻质化、降成本的需求。基于“应力-强度干涉理论”的结构可靠性设计把影响零件工作状态的设计变量都处理成随机变量,应用概率论与数理统计理论及强度理论,可以定量地回答产品在工作中的失效概率或可靠度，更为真实地反映产品的工作状态,因而日益成为机械强度设计的重要方法[4]。尤其对结构强度安全性和结构重量同时具有较高要求的领域，如航空航天装备，结构可靠性设计方法得到越来越广泛的应用[5~8]。

针对上述问题，本文基于动力装置结构强度失效模式，以动力装置结构强度可靠性分析为中心，通过对载荷环境、材料强度的概率分布研究，结合“应力-强度干涉理论”建立动力装置结构强度可靠性计算模型，开展动力装置结构强度可靠性评估与优化。

1 热、机械载荷耦合性分析

图1为动力装置燃烧室结构示意。动力装置弹射点火瞬间，主装药迅速燃烧产生大量高温高压燃气，燃烧室壳体处于热、机械载荷环境下。燃烧室内燃气瞬时温度约1 500 ℃，但是考虑到燃气作用时间极短（小于1 s）且燃烧室内壁面喷涂有隔热涂层，高温燃气对动力装置壳体的加热效果需要进一步分析。

图1 动力装置结构示意

图2为某次动力装置点火试验中实测燃烧室壁温曲线，传感器预埋于隔热涂层下。

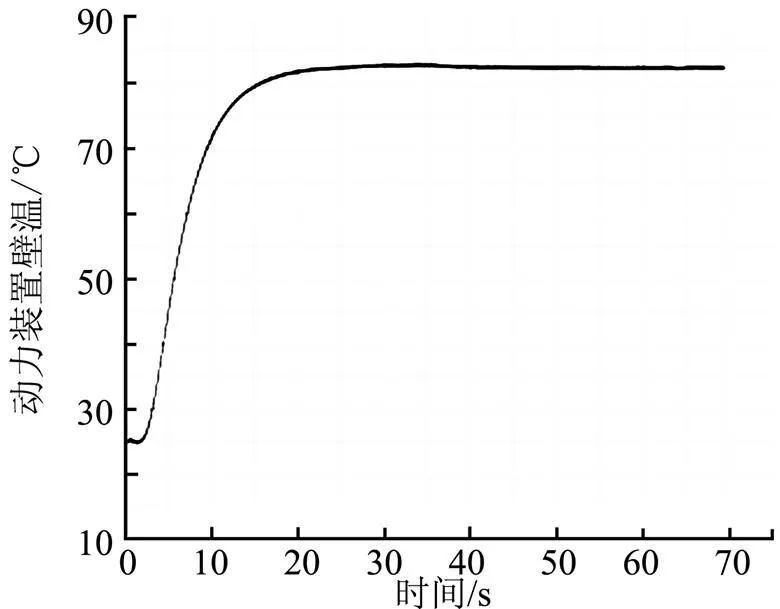
a）70s全程数据

b）3s内数据

图2 燃烧室壁温（环境温度25℃）

由图2可见：燃烧室壁面温度在3 s内基本处于常温状态，之后在残留于燃烧室内的燃气的余温作用下，温度逐步上升，20 s后基本达到热平衡，最高温度约为83 ℃。

考虑到动力装置从点火至装药耗尽、压力卸载全过程不超过1 s，可知：燃气对燃烧室壳体的温度影响远远滞后于建压过程，燃烧室壳体受高温燃气热载荷影响较小，与机械载荷不存在耦合关系，即动力装置壳体的结构强度评估只需要考虑燃气压力影响。

2 动力装置载荷、材料性能的概率分析

结构强度评估的本质是讨论结构应力和材料强度极限的相互关系，在现有动力装置设计体系下，其强度和重量的主要约束条件为：a）载荷边界：当前设计的载荷边界基于动力装置所有影响因素最恶劣工况的同步叠加，这一“同步叠加”缺乏实际的概率分析，对结构强度可靠性的影响尚无深入研究；b）材料性能边界：当前设计的材料强度边界基于材料性能的下限数据，与结构可靠性关联的材料强度性能的概率分布尚无深入研究。本节对上述两个方面开展分析。

2.1 工作内压的概率分析

动力装置燃烧室工作载荷上限为工作压力峰值，决定压力峰值的主要因素有装药初始温度、喷喉直径、装药量等。各因素影响规律如下：

a）装药的燃速性能受温度变化的影响程度由温度敏感系数表征。在一定条件下，药柱初始温度越高，药柱的燃速越高，燃烧室内压力峰值越高。

b）根据空气动力学理论，燃烧室喷喉直径越小，燃气总压越高，即燃烧室内压力峰值越高。

c）在初始温度和喷喉直径相同的条件下，装药量越大，压力峰值越高。

为了获得一致采样条件下的样本数据，本文采集了具有相同装药初始温度、喷喉直径、装药量条件下的共73发数据作为子样。为了包络最恶劣工况，本文装药初始温度选择偏保守的45 ℃极限高温条件。

根据概率统计的相关知识建立如下弹射内压正态分布模型：

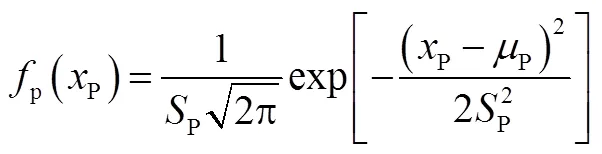
下面根据GB/T4882-2001《数据的统计处理和解释正态性检验》对弹射内压概率模型进行正态性检验，鉴于样本数>50，依据上述标准使用“检验方法”，置信度确定为99%，即显著性水平=0.01。检验过程各统计量计算结果如下：

式中为取样样本的压力值；为1~的常数。

2.2 材料强度的概率分析

3 动力装置结构强度可靠性建模

3.1 应力-强度干涉理论

动力装置结构强度可靠性建模的理论基础是“应力-强度干涉理论”，其内涵如下：

结构失效与否决定于结构强度与应力的关系：强度大于应力时结构安全，强度小于应力时结构失效。实际工程中，应力和强度都是具有某一分布状态的随机变量，把应力和强度的分布在同一坐标系中表示，如图2所示。当强度的均值大于应力的均值时，图2中的阴影部分表示的应力和强度“干涉区”内就可能发生强度小于应力——即失效的情况。这种根据应力和强度干涉情况，计算干涉区内强度小于应力的概率（失效概率）的模型，称为应力-强度干涉模型。

图2 应力-强度干涉模型

基于应力-强度干涉理论，结构可靠度定义为强度大于应力的概率，即：

当强度与应力均服从正态分布时，即：

根据正态分布函数性质，可知安全余量也服从正态分布：

将其转化为标准正态分布函数后可得结构强度可靠度为

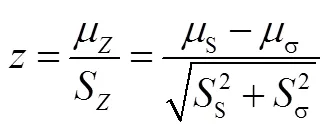
3.2 动力装置结构强度可靠性模型

由于动力装置壳体为精加工而成，壳体直径、高度、厚度等结构尺寸的最大偏差相比于其名义值为小量，变异系数一般不大于0.005（例如动力装置直径变异系数为0.000 1，厚度变异系数为0.001 7），远小于载荷、材料性能的变异系数，对结构强度影响较小，为了简化结构强度可靠性模型，将结构几何参数仍视为确定值。

由正态分布函数性质可得圆筒段应力服从正态分布，即：

其中，

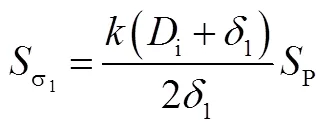
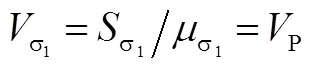
由正态分布函数性质可得椭球封头最大应力也服从正态分布，即：

式中

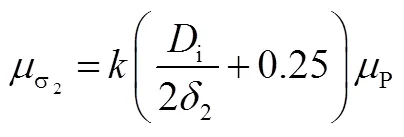
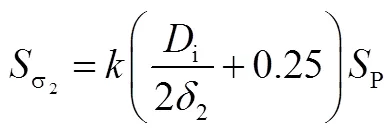
圆筒、封头应力-强度联结系数分别为

式（8）~（17）共同组成了动力装置结构强度的可靠性模型，其中包含了与动力装置结构强度可靠度有关的关键结构参数、载荷参数、材料参数和可靠性指标，可用于动力装置强度可靠性的正向设计或逆向评估。

4 动力装置结构强度可靠性评估与优化

现有动力装置壳体结构强度可靠度指标为不小于0.999，本节基于该设计指标开展动力装置结构强度可靠度的评估和优化。由于壳体内径由装药量决定，因此优化分析中仅以壳体壁厚为变量。基本计算参数如表1所示。

表1 动力装置计算参数

续表1

序号参数数值 4工作压力均值/MPa15.6 5工作压力标准差/MPa2.26 6工作压力变异系数0.145 7壳体内径/mm438 8计算压力系数k1.25

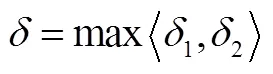
表2 可靠度R与联结系数z

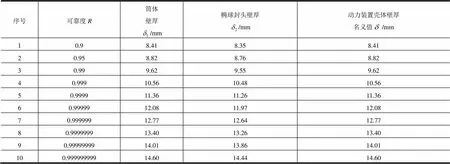
表3 不同强度可靠度下动力装置壳体计算壁厚

根据表3计算结果可得如图4所示的动力装置结构强度可靠度-壁厚关系曲线。从图4中可以看出，当可靠度<0.999时，增加壁厚对于提高强度可靠度作用明显；当可靠度≥0.999时，继续增加壁厚，强度可靠度并不会随之继续显著提高，反而带来不必要的结构重量和成本劣势。现有动力装置壳体结构强度可靠度指标为不小于0.999，设计壁厚为15 mm，实际可靠度远大于设计指标。由表3计算结果可知，动力装置壳体壁厚优化至10.6 mm，可实现减重约30%。

图4 动力装置强度可靠度-壁厚关系

5 结 论

本文通过对动力装置载荷、材料参数的概率分布，结合“应力-强度干涉理论”开展结构强度的可靠性建模分析、评估和优化，得到如下结论：

a）在弹射过程中，高温燃气对动力装置壳体加热效应显著滞后于建压过程，因此动力装置壳体的结构强度设计仅考虑弹射内压载荷即可，材料性能数据可以选用常温数据，无需考虑材料强度在高温下的衰退；

b）在装药初始温度、喷喉直径、装药量一致条件下，弹射内压峰值服从正态分布规律，其置信度高达99%，变异系数约为0.145；

c）基于本文建立的动力装置壳体结构强度模型分析结果，现有动力装置壳体“死重”较大，存在明显的“过安全”设计。基于结构强度可靠度不小于0.999的设计指标，可将动力装置壳体壁厚优化为10.6 mm，实现减重约30%。

[1] 方世武. 筒射型导弹弹射动力装置火药有用能利用系数研究[J]. 导弹与航天运载技术, 2004(3): 18-24.

[2] Sutton G P, Biblarz O.火箭发动机基础[M]. 洪鑫, 等, 译. 北京: 科学出版社, 2003.

[3] 蒋瑞岗. 导弹的弹射与燃气发射器设计[J]. 现代防御技术, 1998, 26(3): 9-16.

[4] 芮强, 王红岩. 结构可靠性设计[M]. 北京: 国防工业出版社, 2014.

[5] 胡昌寿. 航天可靠性设计手册[M]. 北京: 机械工业出版社, 1999.

[6] 刘朋, 张平. 周源泉. 某燃气发生器壳体的结构可靠性分析与评估[J]. 推进技术, 2001, 22(5): 411-414.

[7] Gauthier J, Leduc X, Rauzy A. Assessment of large automaticallygenerated fault trees by means of binary decision diagrams[J]. Journal of Risk and Reliability, 2007(221): 95-105.

[8] Mo Y C. New insights into the BDD-based reliability analysis of phased mission systems[J]. IEEE Transactions on Reliability, 2009(58): 667-678.

Investigation on Structural Reliability of Ejection Launcher

Liu Bao-long, Pan Shuo, Shen Peng, Wu Xin-yue

(Beijing Institute of Space Launch Technology, Beijing, 100076)

In this paper, based on the statistical analysis of experiment data, the probability model of gas pressure peak and material strength was established. The coupling between the thermal and mechanical loads was researched, and the structural reliability model of the ejection launcher was established, and the structural reliability assessment was conducted according to the stress-intensity interference theory. The gas pressure peak was proved to be decoupled from the thermal load, and has a normal distribution while the confidence reached 99%. Contrasted to the structural reliability required, the former ejection launcher casing was "over-safe" designed and can be optimized to have 30% weight reduced.

Ejection launcher; Structural reliability; Probability distribution

1004-7182(2017)06-0072-05

10.7654/j.issn.1004-7182.20170616

V233

A

2017-08-08；

2017-11-07

刘宝龙（1982-），男，博士，工程师，主要研究方向为结构强度与振动控制