数形结合思想方法的发展历程研究
尚影

【摘要】中学数学的发展基本上就是围绕着“数”和“形”这两大基本概念进行的。纵观数学发展史,“数”与“形”最初是一体的,随着社会的进步,人们逐渐把“数”与“形”分离开来,后来人们又发现,数形结合有利于问题的解决,人们又有意识地把“数”与“形”结合起来。
【关键词】数形结合;思想方法;历史演进
【基金项目】阜阳幼儿师范高等专科学校教学研究校级重点项目“在中学数学教学中有效运用数形结合思想方法的教学研究与实践”(编号:ZLGC2017JY011)。
一、数形结合思想方法概述
(一)数学思想方法
1.数学思想。人们对“数形结合思想”的论述不尽相同。
丁石孙认为,数学思想主要指数学研究方法的特点、数学与生产实践的关系,以及数学发展的规律等。
蔡上鹤认为,数学思想是人们通过对生活中数量关系和空间形式的分析而总结出的数学理论的本质。
邵光华认为,数学思想是人们对数学内容的抽象和概括,是数学的本质。
综上,数学思想是人们总结出的数学的本质。数学思想包括很多方面,其中有数形结合的思想。
2.数学方法。数学方法的表述主要有:数学方法是指解决具体数学问题的策略;数学方法是利用数学知识解决问题;数学方法是人们在实践中发现的运用数学思想解决问题的手段。
数学思想与数学方法紧密相连,数学思想强调指导思想,而数学方法强调操作过程。
(二)数形结合思想方法
学术界对“数形结合”的解释各有不同,下面是几种常见的说法。
张同君在《中学数学解题研究》中认为,数形结合是在问题解决过程中,将数量关系和空间形式进行结合,揭示问题的深层结构,从而达到顺利解题的目的。
任樟辉在《数学思维理论》中认为,数形结合是数与形之间整体或局部的迁移。
徐斌艳在《数学课程与教学论》中认为,数形结合是通过抽象思维和形象思维的相互作用,以实现数量关系与图形性质之间的相互转化,将数量关系和图形结合起来研究问题。
数形结合是通过把抽象的数量关系和形象的图形相互转化,从而使抽象问题具体化,以利于问题的解决。
数形结合包含两方面:一是由数及形,利用“形”把问题中的数量关系形象地表示出来,化抽象为直观,用几何方法研究代数问题;一是由形及数,利用代数方法研究几何问题。
二、数形结合思想方法的发展历程
(一)数学萌芽时期的数形结合
在原始社会,数和形是一体的,不分家的。正如周述岐所说:“天上一个太阳,人的一只手有五个指头等等。”此时的数形结合是无意识的,这个时期人们还无法对数与形进行区分。
在数学的萌芽时期,人类在生活中经常进行采集、狩猎活动,后来他们逐渐发现一只鸟、一个果子、一棵树等之间存在共通性,从而抛开事物的物质本身抽象出了数。这就使数的概念从客观事物中分离出来,“数”与“形”出现人类文明发展史上的第一次分离。随着生产活动的进一步发展,社会生活出现了频繁交易,记数变成了必要。记数经历了手指、石头、结绳、刻痕等,后来出现了相应的记数系统。记数又一次将数与形结合起来。这时的数形结合是人类有意识的行为。
(二)古希腊时期的数形结合
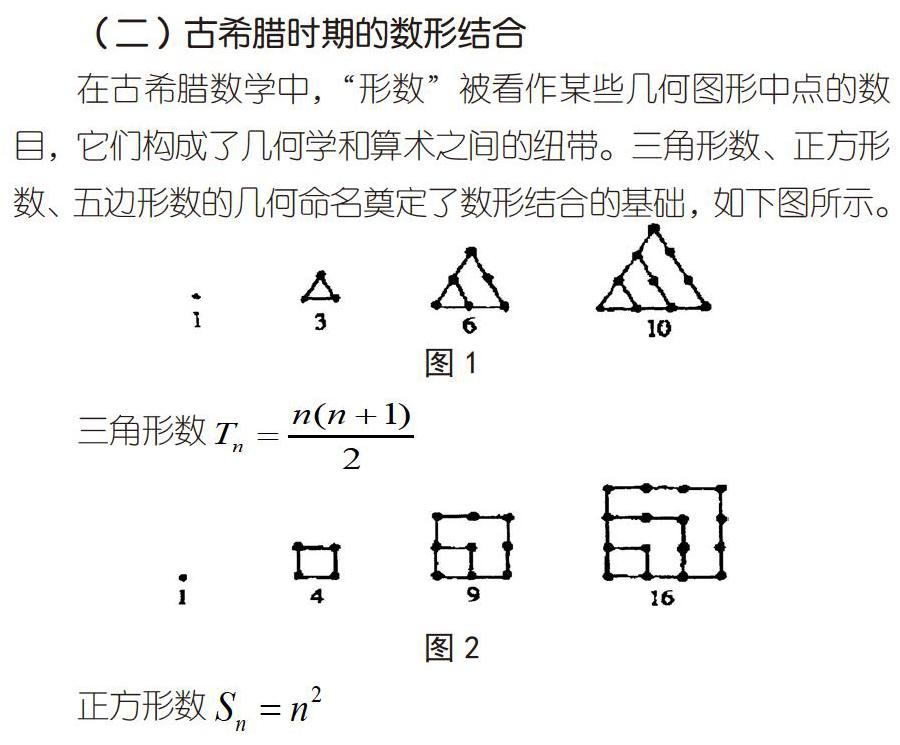
在古希腊数学中,“形数”被看作某些几何图形中点的数目,它们构成了几何学和算术之间的纽带。三角形数、正方形数、五边形数的几何命名奠定了数形结合的基础,如下图所示。
结论1:正方形数是两个相继的三角形数之和,如图4所示。
结论2:第个五边形数等于第个三角形数的三倍加上,如图5所示。
数学以几何学为主要特征的代表作是《几何原本》,这时人们通常从几何的角度去研究等价的代数问题,数形结合的思想促进了代数的发展。如,完全平方数的证明,大正方形的边长为,两个小正方形的边长分别为和,由图可知,大正方形的面积与四部分的面积之和相等,如图6所示。
再如,二项方程的几何解法:已知长度分别为,,的三条线段,由平行线分线段成比例,解得方程,如图7所示;在圆中直径所对的圆周角为直角,根据相似三角形对应边成比例,得方程,如图8所示。
总之,这一时期通常用“形”来研究“数”的关系,毕达哥拉斯学派不接受无理数概念,他们认为有些几何量不能用“数”来度量。
(三)我国古代数学中的数形结合思想
我国古代数学也体现了数形结合的思想,如三国时代吴国的数学家赵爽对勾股定理的证明就采用了数形结合的思想。
赵爽在《周髀算经》注中对勾股定理的证明:“按弦图,又可以勾、股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实。加差实,亦成弦实。”
设勾股形的三边分别为,,,由图和术可得:,将展开,即得勾股定理,如图9所示。
该证明体现了以形证数、数形结合的思想,为中国古代“数形结合”树立了一个典范。著名数学家吴文俊认为,在传统数学中,数量关系与空间形式是并肩发展的。17世纪笛卡尔发明的解析几何正是这种现象的体现。
(四)笛卡尔时代的数形结合
1637年,法国著名数学家笛卡尔创立了解析几何,被认为是近世纪代数发展史上的一个里程碑。数轴的建立使代数与几何联系到一起,数轴上每个点都代表一个实数,且每个实数都能找到一個点和它对应,即点和实数一一对应。后来,笛卡尔又建立了平面直角坐标系和空间直角坐标系,这样一来,就可以在坐标系中解决所有的几何图形问题,在此基础上,他创立了“解析几何学”。解析几何的创立把代数和几何统一起来,数学有了数形结合的新思想,自此,“数”与“形”便真的结合起来了。笛卡尔的坐标系曾被恩格斯称为是“数学的转折”。
(五)现代数形结合
现代数学研究中,人们常用“形”的术语来描述数量关系,指明其几何意义。如非线性规划的各种算法,如果不用几何意义来描写,就无法进一步研究。尤其是一些算法的设计,我们通常先设想一个几何形象,从几何角度进行研究后,再用解析法加以描述,这完全是“数形”结合的研究过程。可见,数形结合是数学发展的必然,它贯穿于数学发展的全过程。
华罗庚先生在《谈谈与蜂房结构有关数学问题》中写道:“数无形时少直觉,形少数时难入微。数形结合百般好,隔离分家万事非。”至此,“数形结合”一词开始得到大家的普遍认可。
三、小结
数形结合给我们提供了一个解决问题的方法,能将复杂问题简单化。数形结合思想方法经历了一个漫长的发展历程,它是随着社会的不断进步而发展起来的,它的每一次发展都代表着人们数学思维方式的改变,是人类文明发展的必然结果。
【参考文献】
[1]藏雷.试析数学思想的含义及基本特征[J].中学数学教学参考,1998(5):2-3.
[2]罗增儒.数学思想方法的教学[J].中学教研:数学版,2004(07):28-33.

