斜直井眼中钻柱横向动态运动非线性模型研究

刘永升， 高德利， 王镇全， 刘 奎

(1. 中国石油大学(北京) 石油工程教育部重点实验室，北京 102249； 2.中国石油大学(北京) 油气资源与探测国家重点实验室，北京 102249)

钻柱作为旋转钻井的关键部件之一，承担着传递地面动力至井底的任务，同时为钻井液循环提供流通通道，它是由一根根特定规格的钻杆通过接头连接而成，钻杆的公称直径小于井眼的直径，所以钻柱在钻压、扭矩的作用下会发生受井眼约束的弯曲、扭转变形，这些变形和位移导致钻柱运动的复杂性，会出现自转、公转、回转等多重耦合非线性运动，运动的不确定性增加，管柱的运动轨迹更加难以预测，同时也增加了控制难度，这直接影响如何改善钻柱的受力状态和磨损方式[1-2]。在斜井或水平井中，由于重力因素的影响，导致钻柱与井壁的接触更加复杂，从而更难以刻画钻柱的运动状态、运动轨迹，也就无法实施行之有效的控制措施避免钻柱的磨穿和键槽卡钻事故[3]。

钻柱的研究通常分为两部分，即静力学分析和动力学分析，前者主要解决钻柱的受力和形变问题，后者主要研究钻柱的动态运动[4]。运动行为主要关注钻柱与井壁的接触行为，也就是钻柱的振动问题，许多研究者在这方面开展了工作。Jansen[5]根据现场实际工况和实钻数据发现：钻柱的旋转会造成井下管柱的剧烈横向振动，基于这个现象，他将钻柱简化为两端轴承约束的偏心转子动力学问题，并考虑流体的影响，研究指出钻柱存在前涡动和后涡动。并且当耦合振动的频率与钻柱的自然频率相近的时候，振幅最大，损害越大。Leine等[6]研究了钻柱系统的不连续性产生的非线性不稳定，并且运用分叉理论解释涡动的出现有助于黏滑振动的减弱。Melakhessou等[7]根据Jansen提出的非平衡质量假设，建立了4自由度模型(径向位移ρ，旋转角θ，切向弯曲角φ，相对扭转角β)，该模型可以表征接头与井壁，钻柱与井壁的弹性碰撞效应，但是无法模拟滑动与滚动现象。Liao等[8]借助Melakhessou等研究成果，兼顾了动子与静子倾斜因素，将模型拓展为5自由度的非线性动态运动方程，同时改进了接触模型，它可以综合反映黏滑、滑动和滚动等接触行为。Khulief等[9]将钻柱离散化为有限的杆单元，每个单元具有12个自由度，并综合考虑陀螺回转效应、扭转和弯曲耦合变形以及重力因素，借助拉格朗日方法和有限元方法建立系统的运动控制方程，该方程证实可以基本表征垂直井中钻柱的运动状态。毋庸置疑，钻柱的运动必然受钻头与地层相互作用的影响，Liu等[10-12]研究考虑钻头-地层互作用规律对钻柱黏滑振动的影响，不同的是这些研究采用了不同的摩擦接触模型，诸如速度平方模型，摩尔库伦摩擦模型以及速度弱化摩擦模型，研究得出，钻头-地层的非线性接触规律是钻柱做不规则运动的根源。国内也有学者进行特定条件下的相关实验和理论研究，韩春杰等[13]采用线性分析法，得出了大位移井钻柱横向振动和扭转振动的频谱方程；管志川等[14]开展了水平井中钻柱非规则运动状态的实验研究，指出钻柱近似“8”字形翻滚摆动；李子丰等[15-16]一直专注管柱静、动力学的研究，侧重通过有限元的方法表征钻柱的动力学行为。值得一提的是上述研究对于垂直井眼中钻柱的运动较为完善，然而由于重力、井眼轨道复杂化等因素，使得斜井或水平段中钻柱运动行为研究更加困难，随着页岩气、非常规油气资源开发比重增加，大位移井、水平井等逐渐成为主要的开发井型，钻柱在井眼中的受力及运动状态颇为复杂，传统垂直井眼钻柱静、动力学应用局限性更加突出，自然而然，非直井中管柱的动力学问题也上升为主要研究难题。

本文基于拉格朗日方程建立了4自由度的非线性动态模型，探究钻柱在非直井眼(斜井段或水平井段)中的动态运动规律，综合考虑了钻柱的扭转、弯曲变形因素以及钻井液流体作用力的影响，并且完善了钻柱与井壁的接触模型，更为真实的模拟黏滑、滑动及纯滚动等接触行为。文中开展了不同井斜角条件下，钻柱运动规律的研究，细致分析了钻柱运动状态及变化规律。该研究渴望为深刻认识斜井中钻柱井下工况提供有益帮助，同时为实施有效措施避免钻柱磨穿和键槽卡给予理论指导。

1 模型建立

1.1 模型简化

图1为井眼中任意两个扶正器之间的一段钻柱，由于重力作用，远离扶正器的钻柱将会贴着井壁躺在低边，如此会导致钻柱与井壁的接触复杂化，在驱动扭矩的作用下，钻柱可能的运动过程由图1显示。为了确定钻柱的真实运动状态，将该模型简化为两个空间独立但是物理上不独立的转子，如图2所示，α为井斜角，图中定子代表扶正器处的钻柱，由于扶正器与井壁间隙较小，为了研究的方便，假设定子满眼，即定子不发生横向位移；动子代表跨中位置处的钻柱，由于钻柱自身质量的非均匀性加之流通泥浆的不稳定性和附着随钻测量仪器，导致钻柱质量偏心，本文参考Jansen的研究，将该处的钻柱考虑为带偏心质量的动子。静子与动子之间通过物理关系表征钻柱的扭转、弯曲等变化。简化模型中，静子受外部驱动扭矩的作用，静子和动子受井壁约束，即横向位移不超过各自与井壁的间隙，同时忽略钻柱的轴向位移。

图1 水平段钻柱形态Fig.1 The morphology of drill-string in horizontal section

图2 钻柱简化模型Fig.2 The simplified model of drill-string

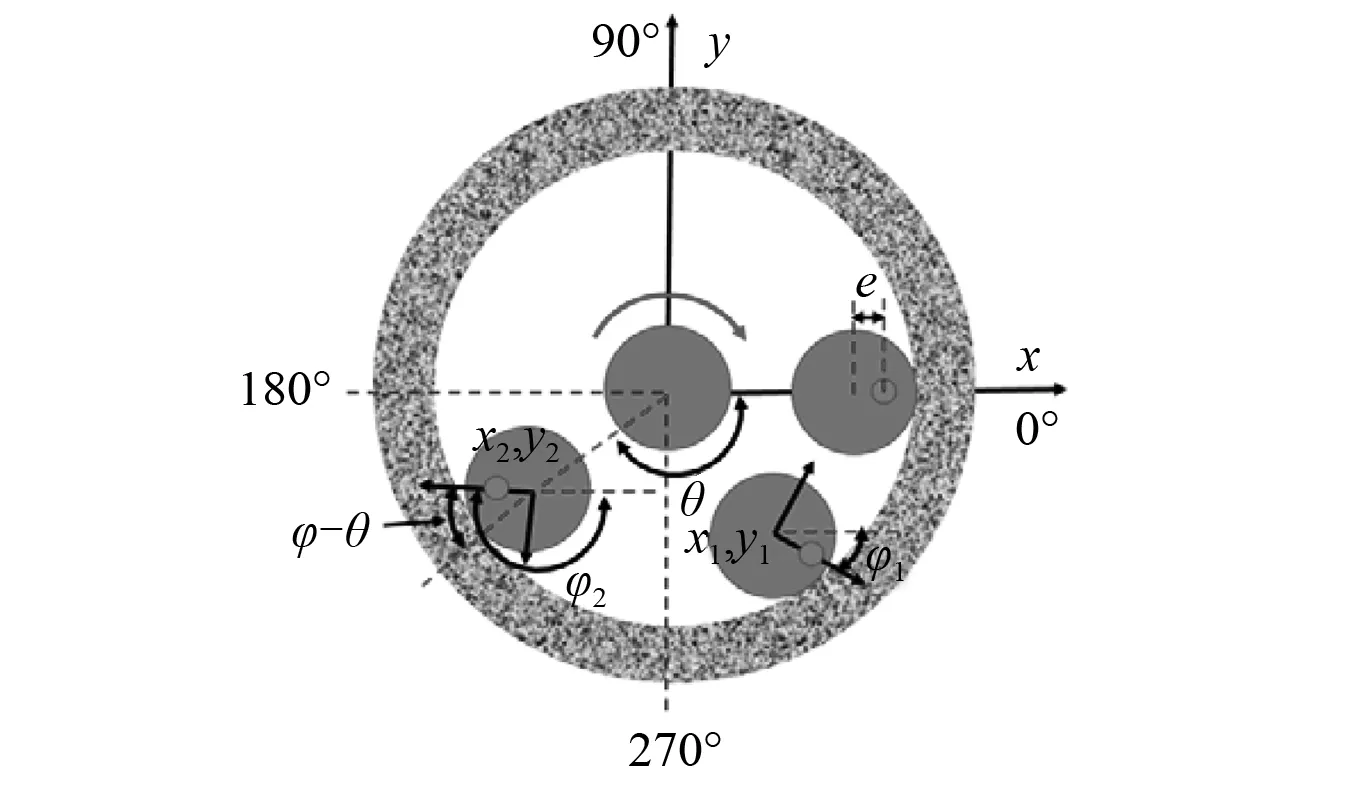
图3 钻柱运动平面简化示意图Fig.3 The schematic diagram of drill-string movement

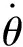
1.2 运动控制方程建立

由上述简化模型，应用Language方程建立系统的运动控制方程，对于非保守系统而言，Language方程表达式为

(1)

式中，L=T-V为Language函数，T和V为系统的动能和势能，对于本文而言

(2)

(3)

(4)

式中：λ为接触判断参数；Ft为切向接触力；Ffx，Ffy为流

体作用于动子的阻力；Mext为驱动扭矩。

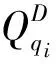
(5)

式中，ct为旋转阻力系数。

将式(2)～式(5)代入式(1)得系统的运动控制方程组

(6)

(7)

(8)

(9)

上述二阶非线性微分方程可以用矩阵表达成一般的振动方程的形式

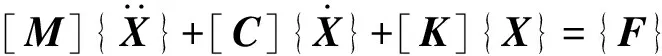
(10)

式中：[M]，[C]和[K]分别为质量、阻尼和刚度矩阵；{F}为外部激励向量。

2 接触模型

钻柱的动态行为是受井眼约束的，其运动范围局限在钻柱与井壁的间隙(δ)之间，也就是说钻柱的径向位移ρ不能超过δ。引入接触判断参数λ识别钻柱与井壁是否发生接触行为，当ρ<δ时，表明二者没有发生接触，所以令λ=0；当ρ≥δ时，表明二者存在接触行为，接触点的相对速度Vrelative可以用来判别接触类型。当Vrelative=0时，表明钻柱与井壁没有相对滑移，而表现为钻柱沿井壁的纯滚动，此时接触的切向力可以通过力和力矩平衡导出式(17)；当Vrelative≠0时，钻柱与井壁接触存在相对滑移，接触切向力用库伦摩擦定律表征，如图4所示，具体计算公式为

δ=0.5(Db-d)

(11)

(12)

(13)

(14)

Ft max=-sgn (Vrelative)·μ·Fnorml

(15)

(16)

(17)

(18)

图4 钻柱与井壁接触行为Fig.4 Contact behavior between drill-string and borehole

3 流体作用力

钻柱内外充满了钻井液，并且伴随强烈的湍流特性，所以在一定程度上影响钻柱的受力和运动。文中钻柱受钻井液作用力参考Fritz[17]基于转动的细长杆在窄间隙流体中的受力模型，表示为

(19)

(20)

式中：mf流体附加质量力；Df为流体的摩擦因数。

4 数值计算与结果

利用本文建立的非线性动态模型开展数值计算研究，应用4阶龙格-库塔数值计算方法求解方程，基本计算参数参考Liu等，具体见表1。本文开展了五种不同井斜角(90°，75°，45°，15°,0°)下钻柱运动规律分析研究，结果分析如下。

4.1 钻柱运动轨迹

图5展示了不同井斜角下动子的运动轨迹图。 从图中对比看出，井斜角对钻柱的运动有着重要影响，随着井斜角的减小，钻柱的重力分量也随之减小，对钻柱的运动影响减弱，直至最终充分发展成为垂直井眼中满眼的回旋运动。图5(a)为水平段(α=90°)钻柱的运动轨迹图，水平井眼中钻柱由于重力完全作用，时刻有倾向井眼低边的趋势，造成了钻柱与井壁接触面积增加，使得二者的接触行为不仅表现为单纯的弹性碰撞，而且夹杂了复杂的摩阻特征，在扭矩的驱使下，钻柱运动稳定后体现为沿旋转方向的30°(240°～270°)扇形区域活动，钻柱随摩擦扭矩的集聚-释放，体现为局部的黏滑、翻滚运动。不难发现，这种局部的摩擦翻滚运动是引起钻柱磨损和发生键槽卡钻的主要原因。随着井斜角的减小，钻柱与井壁局部的黏滑减弱，滑动摩擦距离增长，翻滚幅度拓宽，直至发展成为垂直井眼中均匀随机接触碰撞，如图5(b)～图5(e)所示。

表1 系统参数值

4.2 运动相图对比分析

相图可以真实反应钻柱的运动状态，本文选取了两种不同井斜角下钻柱运动的相图进行分析。图6(a)和图6(b)代表井斜角α=90°，α=15°时钻柱X方向的运动相图，从图中发现，前者出现了明显的“台阶”，表明钻柱与井壁发生了随机的弹性碰撞；后者曲线过渡平滑并且伴随随机“跳跃”，表明钻柱在此发生了由沿井壁摩擦滑动的运动到翻滚的过渡，这与Liao等在垂直井中研究的结果相似。图6(c)(α=90°,Y-方向)表明钻柱在井眼底边做无规则的小幅黏滑翻滚运动，图中δy与钻柱与井壁的间隙δ基本相等，足以证明钻柱运动稳定后倾向井眼低边。图6(c)(α=15°,Y-方向)说明重力因素影响甚微，钻柱的整个运动趋于满眼的回旋运动。

4.3 旋转响应

为了刻画钻柱在驱动扭矩下不同部位的旋转响应，文中提取了不同井斜角条件下扶正器位置(静子)和跨中位置(动子)处的旋转角速度进行对比分析，如图7所示。从图中可以得出，不同井斜角下静子旋转较平稳，主要得益于扶正器的作用，使得钻柱与井壁的间隙变小，导致碰撞、摩擦减少，即使发生接触，幅度变化也甚小。相反，动子的旋转速度受井壁影响颇大。当在水平段中时，由于摩擦扭矩的集聚-释放，动子旋转速度波动幅度较大，而对于近垂直井眼中动子旋转速度表现为低幅高频变化的特性，这和传统垂直井眼中随钻测量数据一致。

图5 不同井斜角下钻柱的运动轨迹Fig.5 The trajectory of drill-string in different inclinations

图7 不同位置钻柱旋转速度变化曲线Fig.7 Rotation speed of drill-string at different positon

5 结 论

本文针对现场实际面临的问题并结合垂直井中钻柱运动的研究成果，应用动力学普遍原理，建立了水平段或斜井段中钻柱运动的4自由度非线性动态模型，基于该模型开展了不同井斜角下钻柱运动特性的分析研究，研究结论如下：

(1)当井斜角为90°时，由于摩阻扭矩较大，钻柱将会沿着自身旋转方向的约30°扇形域的井壁蠕动，并伴随随机的黏滑和翻滚。随着井斜角的减小，局部的摩擦翻滚幅度增加并逐渐扩展成为整个井眼内的带有随机碰撞的旋转运动。

(2)井斜角越大，局部的摩擦翻滚运动越显著，容易引起钻柱磨损和钻杆磨穿，所以在井眼轨道设计时，如果设计允许，应尽量不要增大井斜角。

(3)斜井段和水平段钻柱运动较垂直井段更为复杂，不单是考虑重力因素，更重的是由重力产生的复杂接触行为，比如摩擦蠕动，摩擦翻滚而不仅仅是单纯的弹性碰撞接触。

[ 1 ] HAKIMI H, MORADI S. Drillstring vibration analysis using differential quadrature method[J]. Journal of Petroleum Science and Engineering, 2010, 70(3/4): 235-242.

[ 2 ] MORADI S, RANJBAR K. Experimental and computational failure analysis of drillstrings[J]. Engineering Failure Analysis, 2009, 16(3): 923-933.

[ 3 ] JOSHUA H. Pipe sticking prediction using LWD real-time measurements[C]∥ IADC/SPE Drilling Conference and Exhibition.Fort Worth:Society of Petroleum Engineers, 2016.

[ 4 ] 高德利. 油气井管柱力学与工程[M].东营：中国石油大学出版社，2006.

[ 5 ] JANSEN J. Non-linear rotor dynamics as applied to oilwell drillstring vibrations[J]. Journal of Sound & Vibration, 1991, 147(1): 115-135.

[ 6 ] LEINE R I, CAMPEN D H V. Stick-slip whirl interaction in drillstring dynamics[J].Journal of Vibration & Acoustics, 2002, 124(2): 220.

[ 7 ] MELAKHESSOU H, BERLIOZ A, FERRARIS G. A nonlinear well-drillstring interaction model[J]. Journal of Vibration & Acoustics, 2003, 125(1): 46-52.

[ 8 ] LIAO C M, BALACHANDRAN B, KARKOUB M, et al. Drill-string dynamics: reduced-order models and experimental studies[J]. Journal of Vibration & Acoustics, 2011, 133(4): 3443-3445.

[ 9 ] KHULIEF Y A, AL-NASER H. Finite element dynamic analysis of drillstrings[J]. Finite Elements in Analysis and Design, 2005, 41(13): 1270-1288.

[10] LIU X, VLAJIC N, LONG X, et al. Nonlinear motions of a flexible rotor with a drill bit: stick-slip and delay effects[J]. Nonlinear Dynamics, 2013, 72(1/2): 61-77.

[11] GERMAY C, WOUW N V D, NIJMEIJER H, et al. Nonlinear drillstring dynamics analysis[J]. Siam Journal on Applied Dynamical Systems, 2009, 8(2): 527-553.

[12] RICHARD T, GERMAY C, DETOURNAY E. A simplified model to explore the root cause of stick-slip vibrations in drilling systems with drag bits[J]. Journal of Sound and Vibration, 2007, 305(3): 432-456.

[13] 韩春杰，阎铁. 大位移井钻柱振动规律研究与应用[J]. 天然气工业, 2006, 26(5): 72-74.

HAN Chunjie , YAN Tie. Study on drill string vibrations in extended reach wells and its application[J]. Natural Gas Industry, 2006, 26(5): 72-74.

[14] 管志川，邵冬冬，温欣，等. 水平井眼中旋转钻柱运动特性的实验研究[J]. 工程力学, 2013, 30(5): 340-345.

GUAN Zhichuan, SHAO Dongdong, WEN Xin, et al. Experimental research on motion states of bottom drilling string in horizontal well[J]. Engineering Mechanics, 2013, 30(5): 340-345.

[15] 李子丰. 钻柱涡动理论研究的必由之路—钻井液动力润滑学与钻柱动力学相结合[J]. 石油学报, 2013, 34(3): 607-610.

LI Zifeng. An inevitable way in drill-string whirling research: combination of drilling fluid power lubrication with drill string dynamics[J]. Acta Petrolei Sinica, 2013, 34(3): 607-610.

[16] 李子丰. 油气井杆管柱力学研究进展与争论[J]. 石油学报, 2016, 37(4): 531-556.

LI Zifeng. Research advances and debates on tubular mechanics in oil and gas wells[J]. Acta Petrolei Sinica, 2016, 37(4): 531-556.

[17] FRITZ R J. The effects of an annular fluid on the vibrations of a long rotor, Part 1—theory[J]. Journal of Fluids Engineering, 1970, 92(4): 923-929.