大斜度井眼中钻柱运动特性模拟试验

温 欣, 管志川, 邵冬冬, 周英操

(1.中国石油钻井工程技术研究院,北京 102206; 2.中国石油勘探开发研究院,北京 100083;3.中国石油大学石油工程学院,山东青岛 266580; 4.中国石化华东石油工程有限公司,江苏扬州 225261)

在钻井工程实践中,由于钻柱被严格限制在狭小的井眼内,实际钻进时钻柱的受力状态十分复杂。为了避免钻柱的疲劳破坏,减少井下事故的发生,理清不同工况下钻柱的运动特性就显得尤其必要。为此,国内外专家学者从数值模拟[1-6]、现场实测[7-8]和室内试验[9-11]等方面进行了大量的探索,得到了很多重要的研究成果。直井中的钻柱动力学特性研究开展得相对较早,但随着钻井技术的发展,大斜度井、水平井技术已经广泛地应用于油气田开发,在提高采收率、增大泄油面积等方面发挥了重要作用。钻柱在旋转过程中的运动特性对钻进参数的优选、钻柱服役状态的分析以及井眼轨迹的控制都有重要影响,但对大斜度井中钻柱运动规律还缺乏系统的研究。笔者通过室内模拟试验,分别从转速、钻压和井斜角等方面入手,对大斜度井中钻柱的运动特性进行研究。

1 试验装置及方案

大斜度井钻柱动力学模拟试验装置如图1和图2所示。该装置根据相似原理[12]按照几何比1∶10建造,可通过起升装置调节钻柱的井斜角α,调节范围为75°～90°。模拟试验选取的钻具组合参数为:Φ152.4 mm钻头+Φ120 mm弯螺杆钻具+Φ148 mm稳定器+Φ101.6 mm无磁承压钻杆×1根+LWD+Φ101.6 mm无磁承压钻杆×1根+Φ101.6 mm斜坡钻杆+Φ101.6 mm加重钻杆。试验中钻杆和稳定器采用ABS工程塑料加工制造。

图1 模拟试验装置3D模型和实物Fig.1 3D model and photo of simulation device

钻柱的运动状态由横向位移测量装置进行实时测量,主要由x和y两个方向上的电涡流位移传感器组成,如图3所示。该装置总共4组,分别安装在距离钻头1、3.5、5.5和8 m的位置(图1)。试验过程中通过调节转速n、钻压W以及试验架与地面的夹角θ模拟大斜度井中不同的钻井工况。

图2 模拟试验装置结构示意图Fig.2 Sketch map of structure of simulation device

图3 钻柱横向位移测量装置Fig.3 Measuring device of drillstring lateral displacement

根据文献[13]和[14]中推导的相似准则,钻压、转速和井斜角的关系为

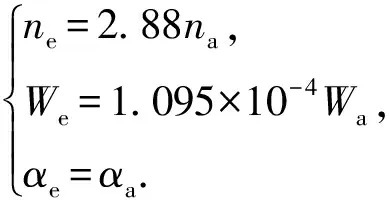
(1)

式中,ne为试验过程中的转速,r/min;na为钻井现场的实际转速,r/min;We为试验过程中采用的名义钻压,kg;Wa为钻井现场的实际钻压,kN;αe为试验过程中井眼的井斜角,(°);αa为钻井现场井眼的井斜角,(°)。

式(1)成立时室内试验结果与工程实际相符,可以将试验中得到的结论用于工程实际。

根据现场实际工况制定了试验方案,参数对应关系如表1所示。若无特殊说明,文中的钻进参数均指试验参数。

表1 试验参数和实际参数对应关系

2 不同转速下钻柱运动特性

井底1 m处的测点离钻头最近,其测量数据对分析底部钻具组合的运动特性和优化钻进参数更具实际指导意义,因此选取该测点进行研究。固定钻压W=1 kg,井斜角α=79°,转速n为50～350 r/min的钻柱振动位移曲线、钻柱运动轨迹和轨迹放大图如图4所示。

从图4可以看出,随着转速的改变,大斜度井眼中钻柱的运动状态具有以下特点:

(1)钻柱横向振动位移曲线在x和y两个方向上始终分离,x方向的位移值为-1～ 3 mm,y方向的位移值为-4～-1 mm。直观地从钻柱运动轨迹图来看,钻柱的运动始终处于井筒的右下部。

(2)随着转速的升高,钻柱的横向振动幅度逐渐增大,摆动越来越剧烈。低转速(50 r/min)时,y方向位移曲线振幅非常微弱,然而在高转速(350 r/min)时,y方向位移曲线振幅显著增加,达到2 mm。从运动轨迹上也可以观察到轨迹的摆动范围随着转速的升高而不断变大。

(3)随着转速的升高,钻柱在井筒中的横向振动频率不断增加。在一段固定的时间(3 s)内,当转速较低时,钻柱完成一次周期性的横向振动耗时较长,相同时间内完成的周期运动次数较少;而随着转速的升高,钻柱完成周期运动的时间明显缩短,位移曲线变得越来越密集,这代表相同时间内完成的周期运动次数不断增加,横向振动频率越来越高。

2.1 转速对钻柱横向振动频率的影响

为了定量研究钻柱的横向振动频率,利用快速傅里叶变换将钻柱振动位移曲线从时域转换为频域,精确地获取钻柱横向振动的频率特征。为了进一步研究钻柱自转频率和钻柱横向振动频率之间的关系,定义无因次频率为

fd=fs/fr.

(2)

式中,fr为钻柱自转频率,Hz;fs为钻柱横向振动频率,Hz;fd为无因次频率。

图4 不同转速下钻柱运动特性曲线Fig.4 Motion curves of drillstring at different rotary speeds

固定钻压W=0.5 kg,不同井斜角情况下钻柱的横向振动频率fs和无因次频率fd随转速升高的趋势如图5和图6所示。

由图5和图6分析得到:

(1)随着转速的增加,钻柱的横向振动频率也逐渐增加。在转速较低(小于250 r/min)的情况下,钻柱的横向振动频率与转速呈现出较好的线性关系;低转速情况下无因次频率约等于1。这表明,钻柱的横向振动频率在低转速时和钻柱的自转频率相等。

(2)随着转速的进一步增加,钻柱横向振动频率发生突变。当转速大于250 r/min时,钻柱的横向振动曲线的斜率变大(图5),同时无因次频率曲线也发生了突变,从fd=1升高到fd=2。这就意味着当转速升高达到某个临界值时,钻柱的横向振动频率突然加倍。该现象在实际的现场钻进过程中意味着振动的加剧,钻柱更加容易受到磨损和破坏。

图5 钻柱横向振动频率随转速的变化Fig.5 Variation of drillstrings vibration frequency with rotary speeds

图6 振动无因次频率随转速的变化Fig.6 Variation of non-dimension vibration frequency with rotary speeds

2.2 转速对钻柱加速度的影响

为了进一步研究钻柱横向振动突然加倍的现象,对钻柱横向运动的加速度进行分析。钻柱横向运动在x方向和y方向的加速度以及实际运动的合加速度分别为

(3)

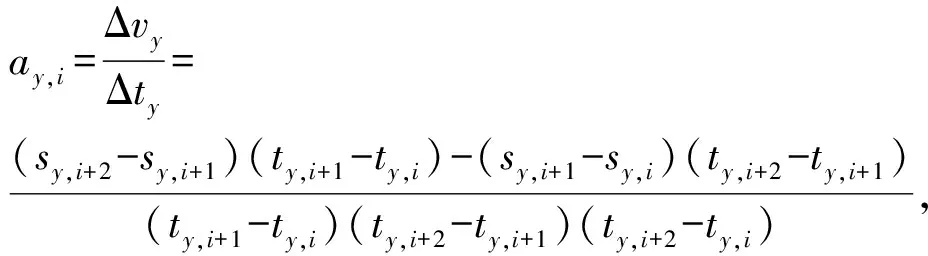
(4)

(5)

式中,ax,i为钻柱i时刻在x方向上的瞬时加速度,m/s2;Δvx为钻柱在x方向上速度分量,m/s;Δtx为钻柱在x方向上时间分量,s;sx,i为钻柱i时刻在x方向上的位移值,m;tx,i为钻柱i时刻x方向上的位移值所对应的时间,s;ay,i为钻柱i时刻在y方向上的瞬时加速度,m/s2;Δvy为钻柱在y方向上速度分量,m/s;Δty为钻柱在y方向上时间分量,s;sy,i为钻柱i时刻在y方向上的位移值,m;ty,i为钻柱i时刻y方向上的位移值所对应的时间,s;am,i为钻柱i时刻实际运动的瞬时加速度,m/s2。

根据式(3)～(5),计算出不同转速下各个时刻钻柱的运动加速度,并计算出测试时间3 s内的平均加速度,结果如图7和图8所示。

图7 钻柱运动加速度随转速的变化Fig.7 Variation of drillstrings acceleration with rotary speeds

图8 平均加速度随转速的变化Fig.8 Variation of average acceleration with rotary speeds

由图7和图8分析可知:

(1)钻柱实际运动的瞬时加速度波动很大,在短时间内发生剧烈变化。以n=50 r/min为例,在t=0.5 s时,钻柱瞬时加速度从12 m/s2迅速降低到约1 m/s2,又迅速升到10 m/s2,表明大斜度井眼中钻柱在旋转的过程中和井壁发生了剧烈的碰撞。

(2)钻柱运动的平均加速度呈现出3个明显的变化阶段。在低转速区域(50～200 r/min),钻柱的平均加速度随着转速的增加缓慢增大,从4.0 m/s2增加到5.7 m/s2,表现出较好的线性规律;从200 r/min开始,加速度进入过渡区域,并在250 r/min时突然增加到8.7 m/s2,远远偏离了低转速时的加速度趋势线;在高转速区域(250～350 r/min),加速随着转速的增加继续增大,且增大的幅度较大。到了350 r/min时,加速度高达11.9 m/s2,约为低转速时的3倍。

通过以上分析可知,随着转速的增加,钻柱的横向振动频率、加速度均增大,并且在高转速(n>200 r/min)时发生突变,此时横向振动变得更加剧烈,钻柱更容易发生破坏。根据表1的对应关系,建议实际钻井过程中现场转速小于69.4 r/min。

3 不同钻压下钻柱运动特性

选定井斜角α=79°、转速n=150 r/min,不同钻压下钻柱的横向振动位移曲线和钻柱实际运动轨迹曲线如图9所示。由图9分析可知:

(1)随着钻压的增大,钻柱的振动幅度无明显变化。首先,从钻柱横向振动位移曲线容易看出,低钻压(0 kg)时钻柱在x方向的横向位移曲线波动幅度约为2 mm,当钻压升高到高钻压(3 kg)时钻柱在x方向的横向位移曲线波动幅度依然维持在2 mm,改变幅度可以忽略;从钻柱的实际运动轨迹看,随着钻压的升高,轨迹的形态、大小均观察不到明显的变化。由于试验条件内所施加的钻压并不足以使钻柱发生较大变形,因此钻压的改变对钻柱的振动幅度无明显影响。

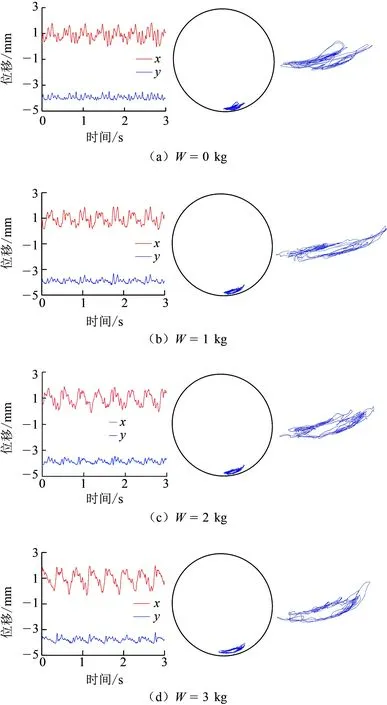
图9 不同钻压下钻柱运动特性曲线Fig.9 Motion curves of drillstring at different WOBs

(2)随着钻压的增大,钻柱的振动频率变化不大。选取x方向的位移曲线进行分析,低钻压(0 kg)时,位移曲线在1 s内出现的波峰数为3个;随着钻压的增加,高钻压(3 kg)时位移曲线在1 s内出现的波峰数同样为3个。这意味着钻柱完成一个周期的振动所需的时间几乎相等。钻压对大斜度井眼中钻柱的横向振动频率无明显影响。

4 不同井斜角下钻柱运动特性

4.1 井斜角对钻柱偏移量的影响

为了探讨井斜角对大斜度井眼中钻柱运动特性的影响,选定转速n=250 r/min、钻压W=0.5 kg,不同井斜角下钻柱的横向振动位移曲线与实际运动轨迹如图10所示。

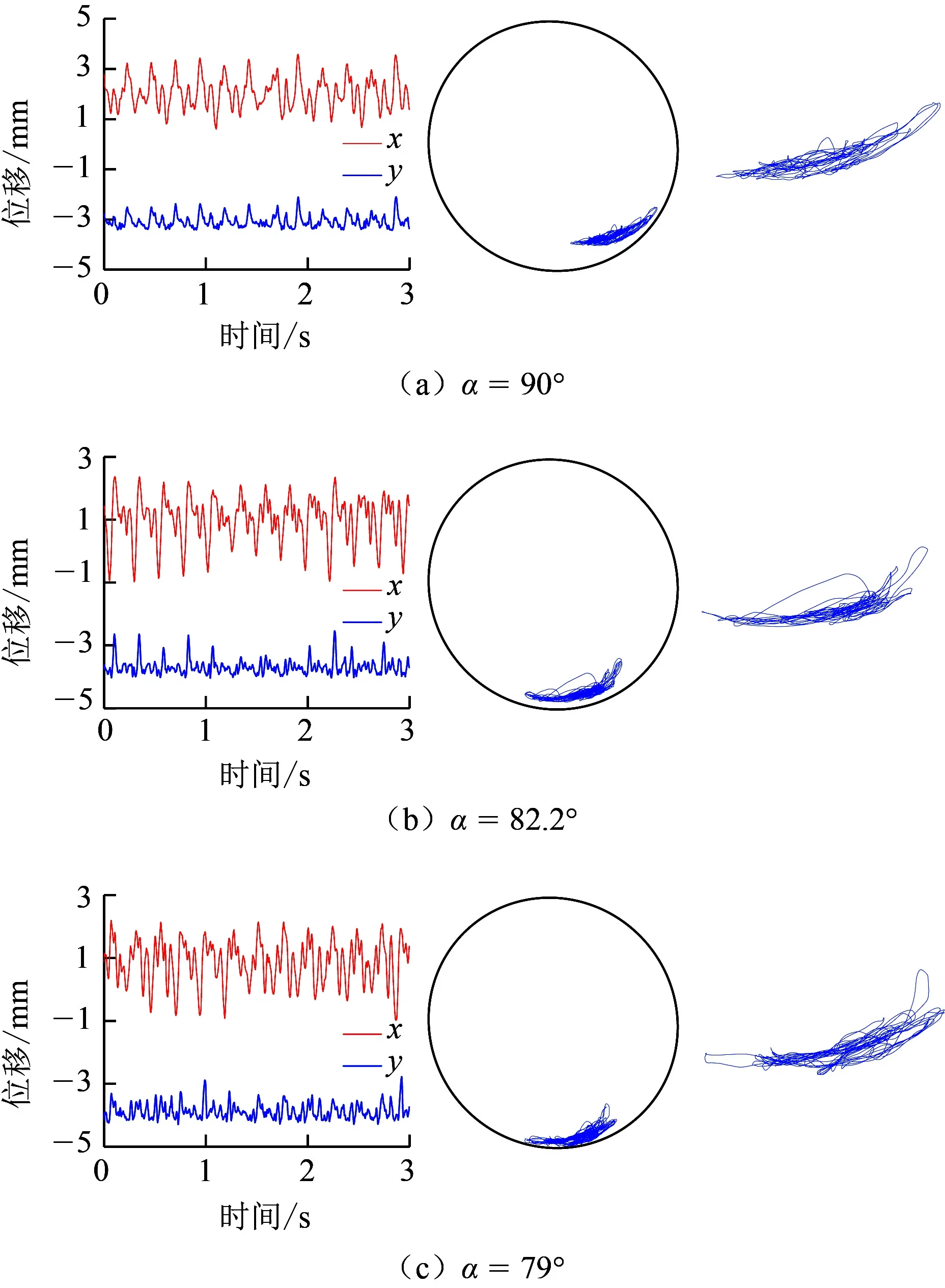
图10 不同井斜角下钻柱运动特性曲线Fig.10 Motion curves of drillstring at different inclination angles

由图10分析可知:

(1)随着井斜角的改变,钻柱横向振动频率无明显变化。无论井斜角如何变化,钻柱位移振动曲线在1 s内出现的波峰数为4个。因此井斜角对于钻柱的横向振动频率没有影响。

(2)随着井斜角的改变,钻柱实际轨迹形态和摆动幅度也无明显改变。3组试验中钻柱实际运动轨迹的形态呈扁平弧形,其轨迹较为相近;x方向上钻柱振动位移均约为3 mm,差别不大。

(3)随着井斜角的增加,钻柱运动轨迹发生了明显的偏移。过模拟井筒的圆心处画一条垂线,观察每一组试验下钻柱的运动轨迹与垂线的横向距离。当井斜角α=90°时,钻柱运动轨迹偏移最为明显,整个轨迹均处于垂线的右侧;而随着井斜角的减小,当α=79°时,钻柱运动轨迹偏移量明显减小,此时运动轨迹有一小部分位于垂线的左侧。

为了能够更加精确地衡量钻柱运动轨迹偏移情况,定义轨迹偏移量,其具体数值等于一段时间内钻柱x方向上的横向振动位移值的算术平均,表示为

(6)

式中,D为轨迹偏移量,mm;N为测试时间内位移测量值的总数。

对每一组试验中的轨迹偏移量进行计算,得到不同钻压和不同转速下偏移量随井斜角的变化曲线如图11所示。

图11 不同钻压和转速下轨迹偏移量随井斜角的变化Fig.11 Variation of trajectory offset at different WOBs and rotary speeds with inclination angels

由图11分析可知:

(1)钻柱的轨迹偏移量与转速和钻压无关。从两幅对比图可以发现,无论转速和钻压如何变化,只要井斜角相同,其对应的轨迹偏移量几乎完全相同。

(2)钻柱的轨迹偏移量随着井斜角的增加而增大,并且增加的趋势越来越快,在水平井时达到最大。当井斜角α=79°和α=82.2°时,虽然轨迹偏移量稍有增加,但是增加的幅度非常微弱,都接近1 mm;当井斜角α=90°时,轨迹偏移量迅速增加到2 mm,增幅明显。

4.2 钻柱偏移机制

假设钻柱没有弯曲,钻柱与井壁为线接触,井斜角为α,井壁和钻柱之间的摩擦系数为μ。大斜度井眼中钻柱始终受到重力G的影响,钻柱在静止状态下位于井壁底部。井壁对钻柱的支撑力为FN,当钻柱以角速度ω在井眼中开始旋转,井壁会给旋转的钻柱施加摩擦力f,如图12所示。则有:

f=μFN=μGsinα.

(7)

旋转钻柱在重力G、支撑力FN和摩擦力f共同作用下沿井壁向上爬升。在爬升的过程中,支撑力FN和摩擦力f逐渐变小,而重力G一直保持不变,那么当钻柱爬升到某一个位置时,又产生向下运动的趋势,最终在井筒的右下部形成动态平衡。

图12 旋转钻柱受力情况示意图Fig.12 Sketch map of force on rotary drill string

井斜角α越大,钻柱所受的支撑力FN也越大,井壁施加在钻柱上的摩擦力f也就越大,钻柱沿着井壁往上爬升的趋势越强。这导致形成的动态平衡的位置也越靠右,最终井眼轨迹的偏移量也越大。当α=90°时,也就是水平井中摩擦力达到最大值,此时的轨迹偏移量最大。

在大斜度井眼中,钻柱的自重G是影响钻柱在大斜度井眼中运动的一个重要因素,这也是大斜度井眼中钻柱运动特性区别于直井的最根本原因。由于钻柱自重G的存在,使大斜度井眼中的钻柱并未产生涡动现象[15],取而代之的是钻柱沿着井壁做有规律的周期性摆动。因此针对大斜度井眼中钻柱运动特性的研究,无论是理论上或是钻井实际中,都不能忽略钻柱自重的影响。

5 结 论

(1)根据相似原理设计并建造了大斜度井眼中钻柱动力学室内模拟试验装置,利用该装置可以模拟大斜度井钻进过程的实际工况,并实现对转速、钻压、钻柱横向位移等参数的实时测量。

(2)转速是影响大斜度井眼中钻柱运动特性的决定性因素,低转速(69.4 r/min)时钻柱的横向振动频率和钻柱的自转频率相等,平均加速度缓慢增加;高转速(86.8 r/min)时钻柱的横向振动频率增加为钻柱自转频率的两倍,平均加速度增加到低转速时的3倍。建议钻井现场转速不超过69.4 r/min。

(3)钻压对钻柱的运动特性影响并不显著,无论施加何种钻压,大斜度井眼中钻柱始终位于井筒的右下部做周期性的摆动,钻柱振动的幅度和频率保持稳定。

(4)井斜角的改变对钻柱的横向振动幅度和频率均无明显影响,钻柱运动轨迹的横向偏移会随着井斜角的增大而增加。在大斜度井中,钻柱的自重对钻柱运动特性的影响不可忽略。

参考文献:

[1] 高宝奎,高德利,谢金稳.钻柱涡动及其应用[J].石油大学学报(自然科学版),1997,21(1):25-27.

GAO Baokui, GAO Deli, XIE Jinwen. Drill string whirling and its application[J]. Journal of the University of Petroleum,China (Edition of Natural Science), 1997,21(1):25-27.

[2] MILLHEIM K K, APOSTAL M C. The effect of bottomhole assembly dynamics on the trajectory of a bit[J]. Journal of Petroleum Technology, 1981,33(12):2323-2338.

[3] LIAN Z, ZHANG Q, LIN T, et al. Experimental and numerical study of drill string dynamics in gas drilling of horizontal wells[J]. Journal of Natural Gas Science and Engineering, 2015,27:1412-1420.

[4] 祝效华,刘清友,童华.三维井眼全井钻柱系统动力学模型研究[J].石油学报,2008,29(2):288-291,295.

ZHU Xiaohua, LIU Qingyou, TONG Hua. Research on dynamics model of full hole drilling-string system with three-dimensional trajectory[J]. Acta Petrolei Sinica, 2008,29(2):288-291,295.

[5] 韩春杰,阎铁,毕雪亮.钻柱横向振动规律及应用[J].大庆石油学院学报,2004,28(1):14-16.

HAN Chunjie, YAN Tie, BI Xueliang. Rules and their application of drilling string lateral vibration[J]. Journal of Daqing Petroleum Institute, 2004,28(1):14-16.

[6] 程载斌,姜伟,任革学.全井钻柱系统多体动力学模型[J].石油学报,2013,34(4):753-758.

CHENG Zaibin, JIANG Wei, REN Gexue. A multibody dynamic1al model of full-hole drillstring system[J]. Acta Petrolei Sinica, 2013,34(4):753-758.

[7] MACPHERSON J D, MASON J S, KINGMAN J E E. Surface measurement and analysis of drillstring vibrations while drilling[R]. SPE/IADC 25777, 1993.

[8] WOLF S F, ZACKSENHOUSE M, ARIAN A. Field measurements of downhole drillstring vibrations[R]. SPE 14330, 1985.

[9] LIAO C M, BALACHANDRAN B, KARKOUB M, et al. Drill-string dynamics: reduced-order models and experimental studies[J]. Journal of Vibration and Acoustics, 2011,133(4):041008.

[10] 管志川,靳彦欣,王以法.直井底部钻柱运动状态的实验研究[J].石油学报,2003,24(6):102-106.

GUAN Zhichuan, JIN Yanxin, WANG Yifa. Experimental research on motion behavior of bottom drill string in straight hole[J]. Acta Petrolei Sinica, 2003,24(6):102-106.

[11] 邵冬冬,管志川,温欣.水平旋转钻柱横向振动特性试验[J].中国石油大学学报(自然科学版),2013,37(4):100-103.

SHAO Dongdong, GUAN Zhichuan, WEN Xin. Experiment on lateral vibration characteristics of horizontalrotary drilling string[J]. Journal of China University of Petroleum (Edition of Natural Science), 2013,37(4):100-103.

[12] 李之光.相似与模化:理论及应用[M].北京:国防工业出版社,1982.

[13] 史玉才,苑燕燕,武春芳.应用相似方法模拟研究底部钻具组合的公转运动规律[J].广西大学学报(自然科学版),2006,31(B06):159-162.

SHI Yucai, YUAN Yanyan, WU Chunfang. Setting up a simulate device on motion behavior of bottom-hole assembly according to similitude principles[J]. Journal of Guangxi University(Natural Science Edition), 2006, 31(B06): 159-162.

[14] 邵冬冬,管志川,温欣,等.水平井段旋转钻进时钻头侧向力及钻进趋势试验研究[J].中国石油大学学报(自然科学版),2014,38(3):61-67.

SHAO Dongdong, GUAN Zhichuan,WEN Xin, et al. Experimental study on bit side force and drilling tendency in a horizontal well using rotary drilling technique[J]. Journal of China University of Petroleum(Edition of Natural Science), 2014,38(3):61-67.

[15] 章扬烈.钻柱运动学与动力学[M].北京:石油工业出版社,2001:30-89.