超临界CO2压裂井筒流动模型及耦合求解
李小江, 李根生, 王海柱, 田守嶒, 宋先知, 陆沛青, 刘庆岭
(1.中国石油大学油气资源与探测国家重点实验室,北京 102249; 2.中国石化石油工程技术研究院,北京 100101)
CO2可以在较低的温度(304.2 K)和压力(7.38 MPa)下达到超临界态,是一种优质的无水压裂液[1-6]。考虑到超临界CO2独特的物理性质[2,7],在其压裂过程中,井筒热源项的组成及其对CO2流体流动和传热特性的影响尤为重要,需要开展深入研究。目前,针对井筒流动和传热问题,主要有解析[8-12]和数值[13-18]两种研究方法。笔者在CO2流体物性模型的基础上,结合流体力学基本方程组,建立考虑不同类型热量源汇的超临界CO2压裂井筒流动解析模型,通过井深和径向方向的迭代计算,实现模型的双重耦合数值求解,并利用该模型研究超临界CO2压裂井筒流动与传热特性。
1 井筒流动数学模型
1.1 基本假设
假设:井筒内为稳态传热,地层为非稳态传热;油管外传热仅考虑径向传热;忽略辐射传热和相变潜热;油管、套管与井眼同心;井眼规则,水泥胶结质量良好,无气窜。
1.2 流体物性模型
超临界CO2流体的物性参数是井筒流动计算的基础参数,为保证井筒温度压力的精确计算,须选用精度较高的流体物性模型,将其与井筒温度场和压力场进行耦合计算。为此,采用适用于CO2精度较高的S-W方程[19]计算CO2的密度和比热容等热力学性质,采用Fenghour和Vessovic等[20-21]模型计算黏度和导热系数等输运性质。
1.3 压降模型
以井筒中流体为研究对象,任意截取一段微元体,针对一维稳态流动,质量守恒方程和动量方程[22]为
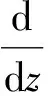
(1)

(2)
式中,z为井深,m;ν为流速,m/s;g为自由落体加速度,m/s2;θ为井斜角,(°);τw为井壁(油管壁)处剪切应力,Pa;d为油管内径,m;Ap为油管内截面积,m2。
将质量守恒方程代入动量方程,并对壁面摩擦力项进行代换,可得CO2流体在井筒中向下流动的压降方程为
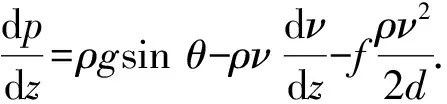
(3)
式中,f为Darcy阻力系数。
阻力系数f的精确求解是压力预测的关键,笔者采用Wang等[23]提出的专门适用于超临界CO2摩阻系数的经验计算公式,据文献报道其在常用雷诺数范围内的计算误差小于3.08%。
1.4 传热模型
针对开放系统,考虑稳态流动的能量守恒方程[22]为
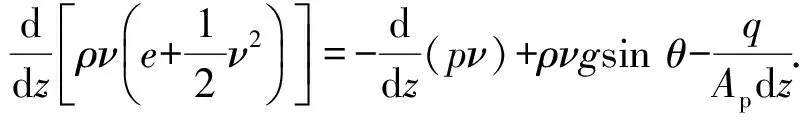
(4)
式中,e为单位质量CO2流体的内能,m2/s2。
井筒与地层之间的热量传递可以用热量传递方程表征[8]为
q=πdU(Tt-Tei)dz.
(5)
式中,q为径向方向上油管内流体与地层之间传递的热量,J/s;U为总传热系数,W/(m2·K);Tt为油管内CO2流体温度,K;Tei为原始地层温度,K。
结合质量守恒方程和热量传递方程,可将能量方程化简为
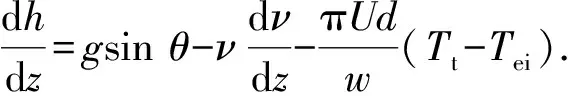
(6)
式中,h为CO2流体的焓,m2/s2;w为质量流量,kg/s。
考虑单一油管+套管的井身结构,总传热系数表达式为
(7)
式中,ht为油管内CO2流体的强迫对流换热系数,W/(m2·K);ks为油/套管导热系数,W/(m·K);dto为油管外径,m;ha为环空流体的自然对流换热系数,W/(m2·K);dci为套管内径,m;kc为水泥环导热系数,W/(m·K);dwb为井眼直径,m;dco为套管外径,m;f(t)为地层非稳态传热的无因次温度函数[10],该函数是由拉普拉斯变换求解傅里叶导热定律得来,表示井壁处温度随时间的变化关系,可用于表征地层非稳态传热过程,而不必对时间域进行离散计算,其具体表达式可参考文献[10];ke为地层导热系数,W/(m·K)。
相比常规流体,CO2对流需要考虑浮升力的影响,因而采用Liao和Zhao[24]提出的温度压力适用范围较广、精度较高的CO2圆管向下流动强迫对流换热系数计算公式。环空自然对流换热系数采用改进的Dropkin和Somerscales[25]关联式。通常情况下,油管和套管壁的热阻可近似忽略不计,而环空自然对流换热和水泥环热阻则相对比较重要,但是CO2对流换热系数的计算需要考虑流体和管壁之间的温度差异,因而模型不能忽略油管和套管壁热阻。
考虑比焓梯度方程为
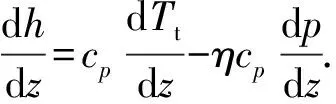
(8)
结合压降方程(3),可得CO2流体在井筒中向下流动的传热方程为

(9)
式中,pfr为CO2流体摩阻损失,Pa;η为焦耳-汤姆逊系数,K/Pa;cp为比定压热容,J/(kg·K)。
2 模型双向耦合求解
超临界CO2的物性参数对温度和压力的变化非常敏感,进行温度或压力某一元素的求解时,必须同时考虑另一元素的变化对物性参数的影响,为提高计算精度,模型首次采用双向耦合求解。即在井深方向上,物性模型、压降模型和传热模型三者进行耦合迭代求解;在径向方向上为了精确求解传热模型的关键参数——总传热系数,需要同时耦合油管-环空-地层,以计算不同管壁的内外温度,并将其同井筒内温度和压力一同迭代求解。
考虑到超临界CO2物性参数沿井深方向存在显著差异,将井筒沿井深方向划分成N个计算单元,计算流程如图1所示。
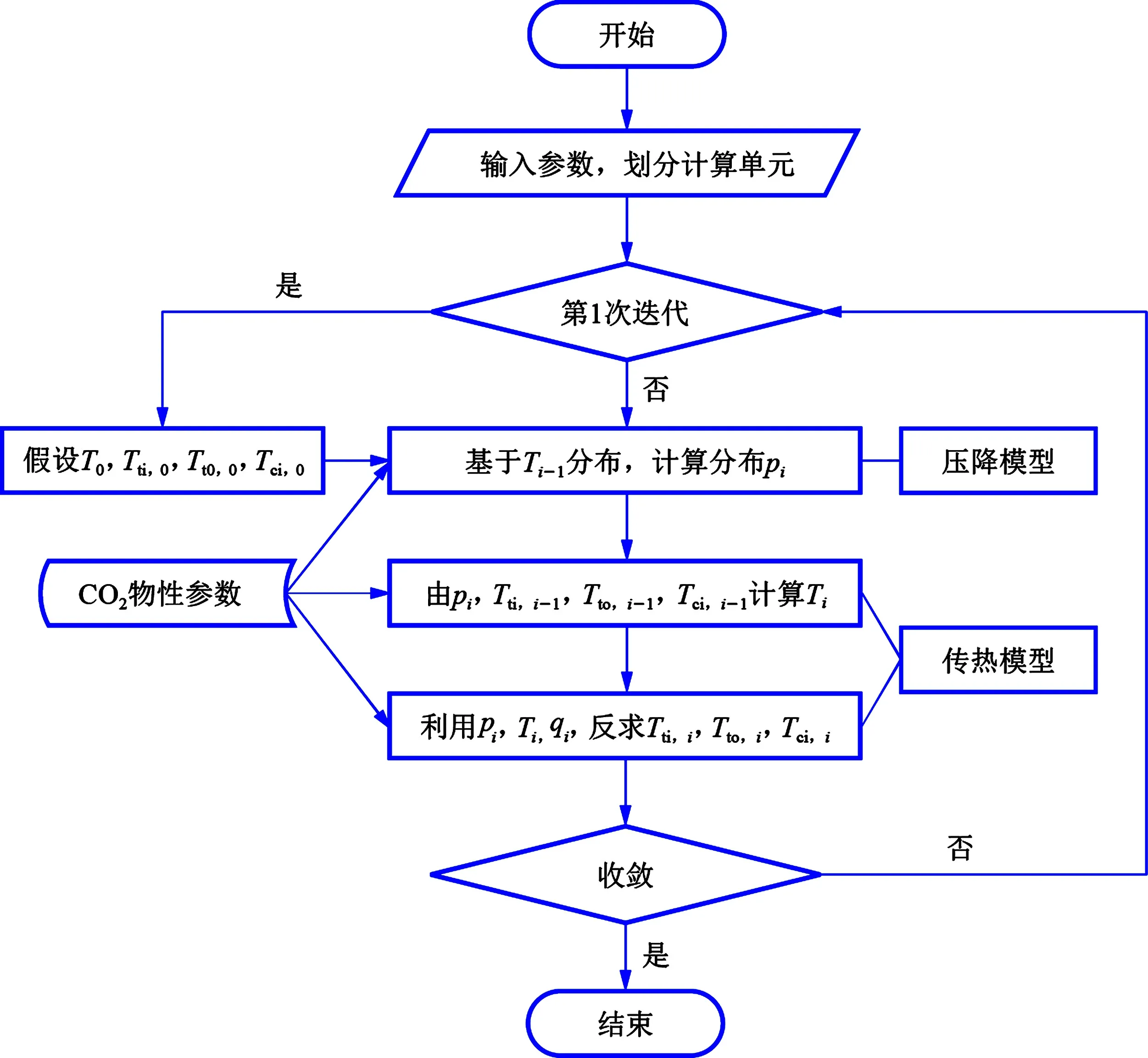
图1 计算流程Fig.1 Flowchart of algorithm
图1中下角i和i-1代表迭代次数,下标ti、to和ci分别表示油管内壁、油管外壁和套管内壁。
3 模型对比与验证
为了验证模型的正确性,从理论模型对比与现场实测数据验证两个方面对本文中模型的推导过程和模型精度进行验证。
3.1 模型对比
相比压降模型,传热模型涉及参数较多,模型更为复杂,因此主要进行传热模型的对比分析。
Ramey[8]和Kabir等[10]最早提出并发展了基于非严格能量守恒的井筒传热经典模型,但这些模型均不考虑相变、摩擦以及气体膨胀等效应产生的热量,因而是一种无源汇的、简化的能量守恒模型。热量传递示意图如图2所示。
如图2所示,模型以长度dz的井筒单元为计算单元,根据井深方向与径向方向热量传递守恒的原则,给出井筒热量平衡方程为
qt(z)-qt(z+dz)=-qtf.
(10)
式中,qt(z)为单位时间内在井深方向流入计算单元的热量,J/s;qt(z+dz)为单位时间内在井深方向流出计算单元的热量,J/s;qtf为单位时间内在径向方向井筒内流体与地层之间的热量传递,J/s。
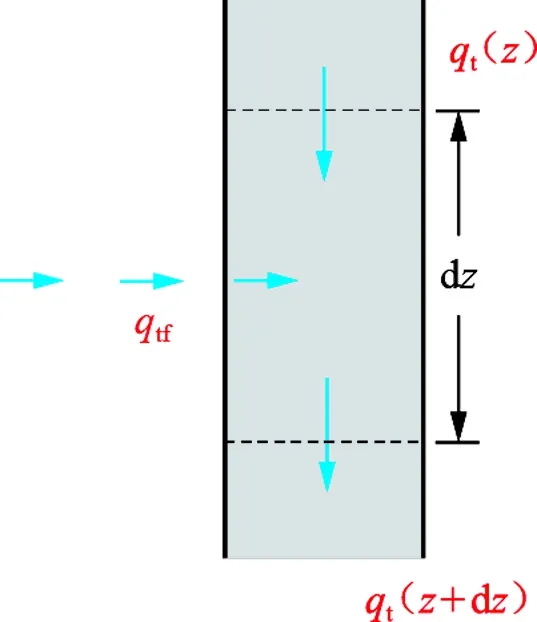
图2 热量传递示意图Fig.2 Sketch map of heat transfer
基于井筒热量平衡方程(10),推导可得井筒流动的传热模型为
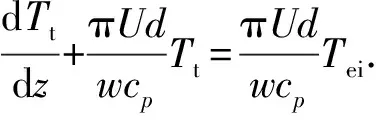
(11)
模型推导过程详见文献[8]和[10],同时亦可参照本文中2.3进行类似推导。对比式(9)和(11)可以发现,Ramey等的模型中没有考虑摩擦和气体膨胀与做功等产生的热量,因而缺少摩擦生热项、焦耳-汤姆逊效应项以及气体膨胀做功项等热量源汇项。为此,将摩擦生热源项加入Ramey等的模型中,热量平衡方程变为
qt(z)-qt(z+dz)+qfr=-qtf.
(12)
式中,qfr为单位时间内计算单元内流体与管壁等摩擦而产生的热量,J/s;类比电流做工生热(P=UI),摩擦生热项可用qfr=Δpfrwv[26]表示,其中Δpfr为计算单元的摩阻压降,Pa;wv为体积流量,m3/s。
同样,可得考虑摩擦生热的井筒传热模型为

(13)
通过类似方法,气体做功项和焦耳-汤姆逊效应项亦可添加到Ramey等的热量平衡方程,最终可以得到与式(9)完全相同的方程。不同的推导方法得到相同的结果,说明本文中模型推导过程的正确性。
3.2 模型验证
国内超临界CO2压裂尚处于起步阶段,目前只开展了少数先导性压裂试验,因此以一口超临界CO2注入井为例[27]进行模型验证,该井的基本参数为:井深3 100 m,油管内径62 mm,油管外径73 mm,套管内径124.37 mm,套管外径137 mm,井筒直径215.9 mm,地表温度288.15 K,地温梯度0.03 K/m,地层密度2 600 kg/m3,地层质量热容837 J/(kg·K),地层导热系数2.09 W/(m·K),油套管导热系数44.7 W/(m·K),水泥环导热系数0.52 W/(m·K),排量55.4 t/d,注入压力24.5 MPa,注入温度253.15 K,注入时间13 h,水泥返高2 074 m,完井液密度1 000 kg/m3,完井液质量热容4 186.8 J/(kg·K),完井液导热系数0.6 W/(m·K),完井液黏度0.6 mPa·s。
基于现场数据,采用本文中模型计算得到的井筒温度与压力剖面如图3中实线所示。
由图3可知,在注入压力24.5 MPa、注入排量55.4 t/d的条件下,井筒内CO2的流动摩阻很小,井筒内CO2流体压力随井深近似呈线性增加,并在井底达到最大值52.46 MPa,与实测值52.02 MPa的相对误差为0.85%;而文献[27]的计算压力值低于本文的计算结果,计算井底压力为50.06 MPa,与现场实测值的相对误差为3.77%。
在CO2的注入温度为253.15 K的条件下,随着井深的增加,井筒油管内CO2温度也逐渐增加,且从井口开始,温度的增速逐渐变缓,直至井深1 000 m以后,温度增加速度基本保持不变,与地温梯度相当。这是因为CO2注入排量较小,在井口附近,流体温度与地层温度差异较大,因而两者之间的热量交换大;随着井深的增加,温差逐渐降低,直至达到热量交换平衡状态。计算井底温度为374.53 K,与实测温度374 K的相对误差为0.14%(若温度单位为摄氏度,则相对误差为0.52%)。虽然文献[27]计算得到的井底温度与本文一致,但其上部井筒温度预测值显著高于本文中的计算结果,更接近地层温度,井筒温度与地温的差值随井深的增加先减小后增大,不符合实际的井筒传热规律,此外对井筒温度的过高估计也是导致井底压力计算值低于实测值的原因之一。
此外可知,图3中的油管内CO2流体与油管内外壁温度相差很小,但与套管内壁温度存在一定的差距。上述现象表明油管热阻要远小于环空流体热阻,在计算井筒温压场时应充分考虑环空流体对井筒传热的影响,尤其是在环空中充满绝热性能较好的流体的工况下。
综上所述,模型计算得到的超临界CO2压裂过程中的温度压力场,相比于现场实测数据,井底压力误差小于0.85%,井底摄氏温度误差小于0.52%,且井筒流动规律符合实际工况条件下的温度压力场变化规律。由此,可认为模型精度较高,可以开展相应的规律研究。

图3 井筒压力和温度剖面Fig.3 Wellbore pressure and temperature profile
4 井筒传热特性分析
通过与Ramey等经典传热模型的对比分析可知,Ramey等模型未考虑摩擦生热、气体膨胀或压缩做功以及焦耳-汤姆逊效应等热量源汇项。重点考察在超临界CO2小排量压裂(试压,或注CO2)和大排量压裂两种工况下,不同类型的热量源汇项对井筒流动和传热特性的影响。
图4为小排量CO2注入压裂过程中的井筒压力和温度剖面,其中注入排量为55.4 t/d,即0.035 m3/min。
由图4可知,热量源汇项对井筒压力基本无影响,但对井筒温度有一定影响。摩擦生热对井筒传热贡献很小,图4中蓝线与黑线基本重合;焦耳-汤姆逊效应的影响也较弱;相比之下,气体做功对井筒传热贡献较大,考虑气体做功的温度要高于不考虑气体做功的温度,两者温度差异在井底达到最大,在本算例中为2 K,相对误差为0.53 %。一方面由于CO2注入排量较小,因而摩阻较低,摩擦生热对井筒温度影响很小;另一方面,由上到下,井筒压力逐渐增加,对气体的压缩效应逐渐增强,因而外界对气体做功转化为气体内能,温度上升;并且随着井深的增加,CO2流体温度逐渐升高,接近地层温度,导致流体密度降低,可压缩性增强。因此考虑和不考虑气体做功两种情况的温差逐渐增大,在井底达到最高值。
图5为大排量CO2压裂过程中的井筒压力和温度剖面,其中排量为3 200 t/d,即1.9 m3/min,注入压力为60 MPa。
由图5可知,在CO2大排量压裂施工过程中,井筒温压呈现与CO2小排量注入完全不同的规律。随着井深的增加,压力先增加后降低,摩擦生热对井筒压力的影响最大,气体做功次之,焦耳-汤姆逊效应最小。井筒温度要显著低于原始地层温度,摩擦生热对井筒温度的影响也显著强于其他因素,考虑摩擦生热的情况同不考虑摩擦生热相比,井底温度相差15 K,相对误差为5.27%;相比CO2小排量注入过程,气体做功的影响反而减小;同样,焦耳-汤姆逊效应影响最弱,基本可以忽略不计。
上述现象的原因在于:一方面由于CO2排量较大,流动摩阻损失要高于重力势能对压能的转化部分,压力出现反转,而不是持续增加,因此需要提高井口注入压力;另一方面,流动摩阻的提高也增加了摩擦生热产生的热量,因而考虑摩擦生热的井筒温度提高、密度降低,导致实际井筒压力降低。气体做功对井筒温度的影响减弱,因大排量压裂导致摩阻损失增加,井筒的压力区间变化范围缩小,随着井深的增加,压力增速变缓甚至出现反转,气体膨胀和压缩效应减弱并相互抵消,对井筒温度的贡献减小。
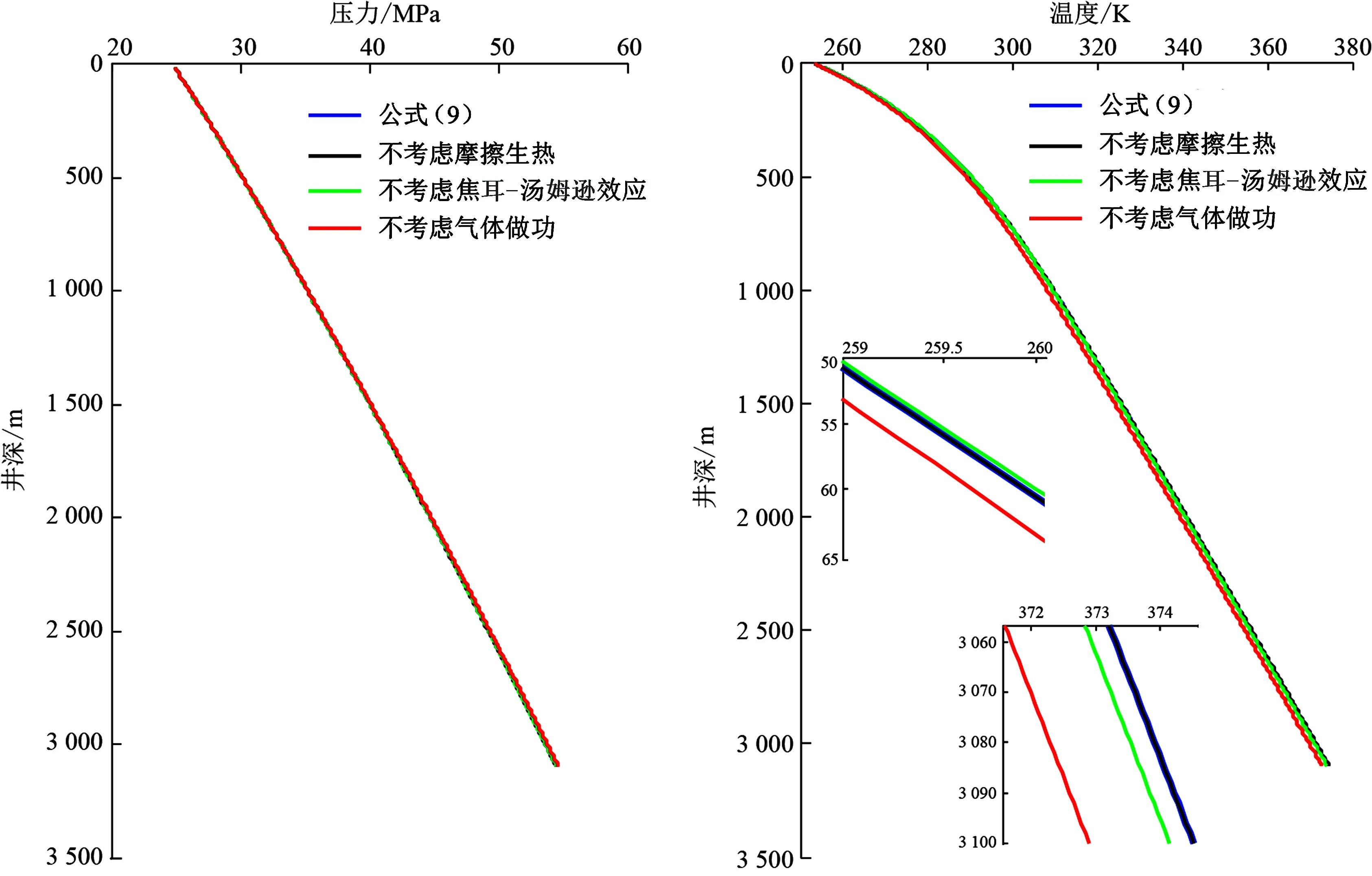
图4 小排量下井筒压力和温度剖面Fig.4 Wellbore pressure and temperature profile at low flow rate
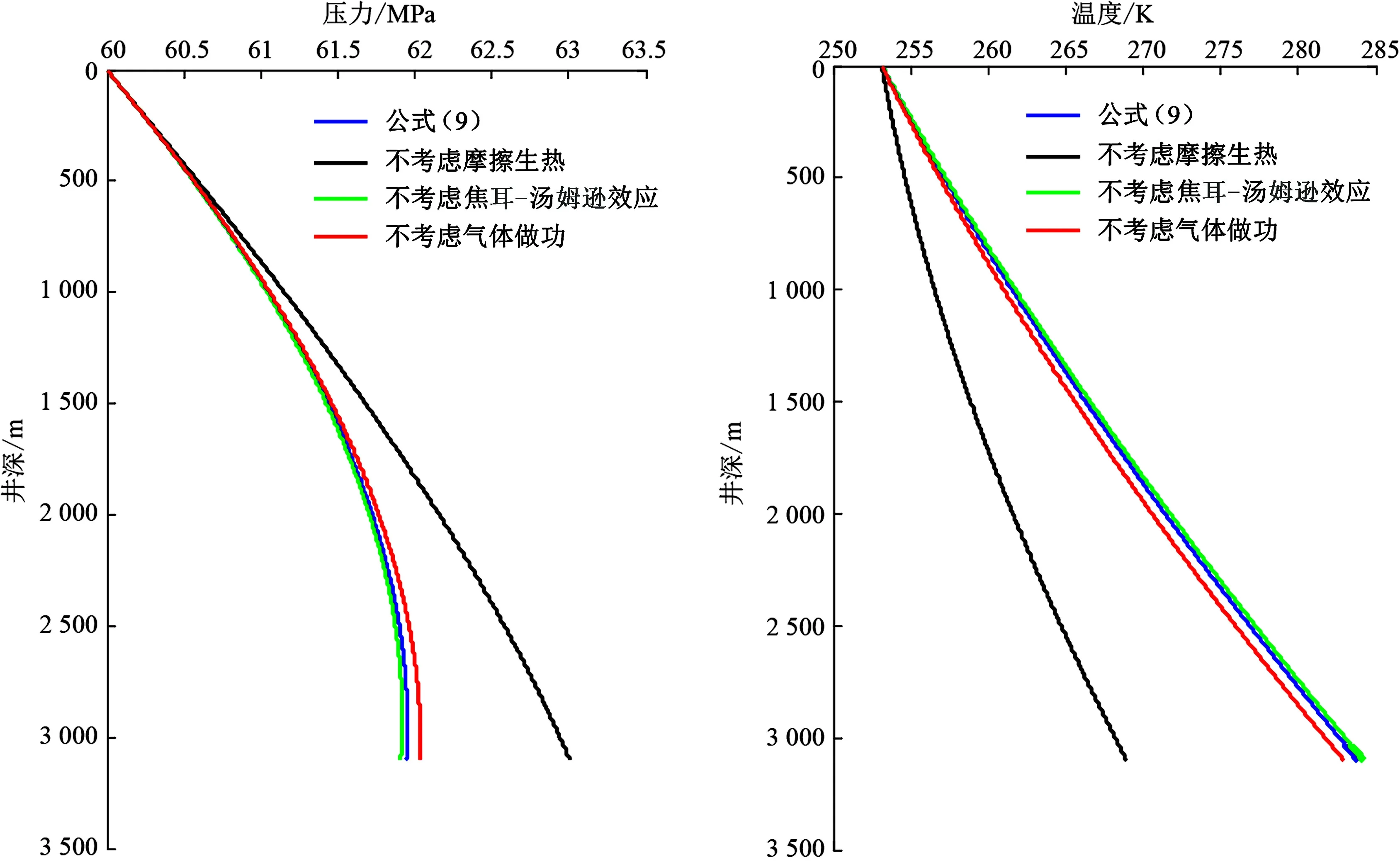
图5 大排量下井筒压力和温度剖面Fig.5 Wellbore pressure and temperature profile at large flow rate
井底压力和温度随排量的变化如图6所示。虽然热量源汇项对井底压力的影响较小,各曲线重合度较高,但仍可观察到小排量下不考虑气体做功曲线及大排量下的不考虑摩擦生热曲线与其他曲线的差异。随着排量的增加,气体膨胀或压缩做功对井筒温度的贡献先增大后减小;摩擦生热对井筒温度的贡献则持续增加,并在排量为1.37 m3/min时超过气体做功,成为主控因素;焦耳-汤姆逊效应在研究排量范围内对井筒温度贡献最小,与实际温度最大相对误差不超过1.75%。当排量高于0.6 m3/min时,井底温度开始低于临界温度,因此需要采取提高井口注入温度等措施提高井底温度,使CO2达到超临界状态。
通过以上分析可知,不同排量下,气体膨胀或压缩做功对井筒流动和传热的影响较大,在工程计算中不能忽略;大排量超临界CO2压裂过程中,摩擦生热效应显著增强,不能忽略其对井筒流动和传热的影响,这也与文献[18]的研究结论一致。绝大多数情况下,焦耳-汤姆逊效应对井筒流动和传热的影响较小,在工程上可根据计算需求选择性忽略。在现场实际计算时,根据不同工况忽略影响较小的热量源汇项,在保证计算精度的同时减少计算量。
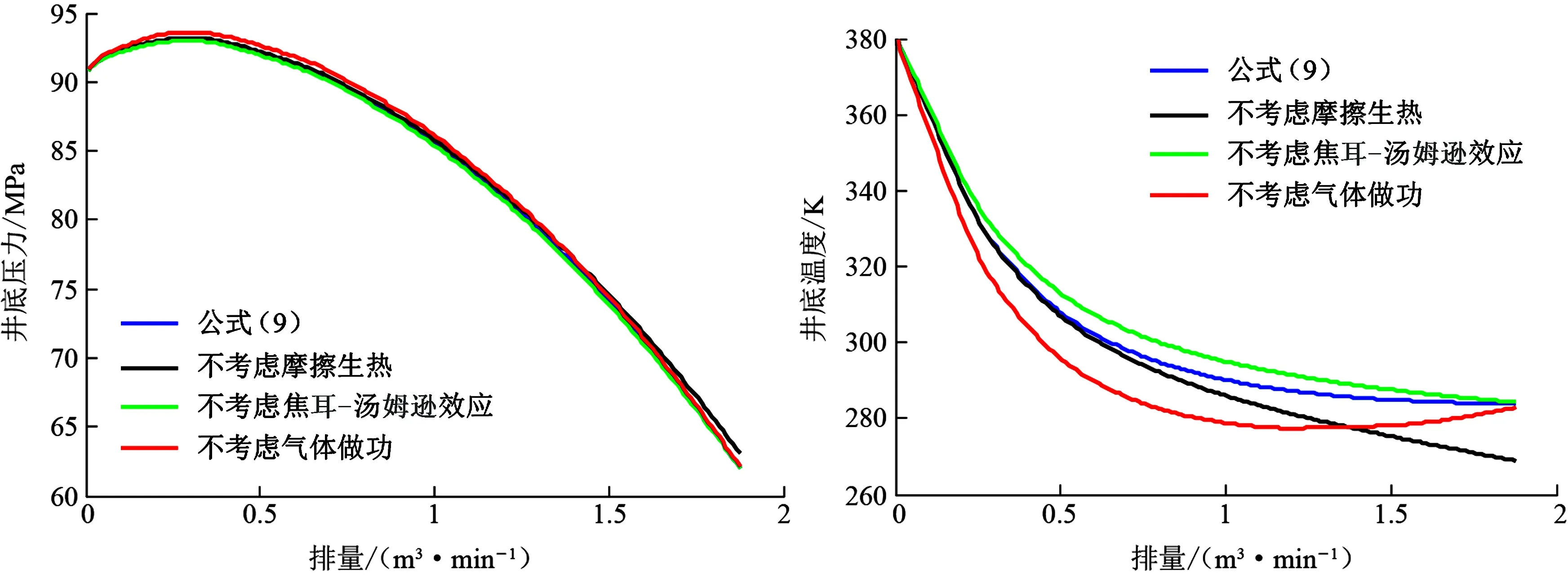
图6 井底压力和温度随排量的变化Fig.6 Variation of bottomhole pressure and temperature with flow rate
5 结 论
(1)在考虑CO2密度等物性参数变化的基础上,联立质量守恒方程、动量方程和能量守恒方程,建立了考虑热量源汇项的超临界CO2压裂井筒流动模型。通过温度和压力以及油管-环空-地层的耦合迭代计算,实现了井深和径向方向的双重耦合数值求解,得到了超临界CO2压裂过程中的井筒温度和压力分布。
(2)通过与Ramey经典传热模型对比分析,验证了模型推导的正确性;同时计算得到的井底温度和压力与现场实测值的误差均小于1%,能够满足工程计算的需要。
(3)热量源汇项在不同排量下对井筒流动和传热的影响程度不同。在CO2小排量注入压裂过程中,气体做功对井筒流动和传热的影响不能忽略;而在CO2大排量压裂过程中,需要同时考虑摩擦生热和气体做功的影响;不同排量下,焦耳-汤姆逊效应影响较弱,工程计算上可忽略。
参考文献:
[1] WANG H, LI G, SHEN Z. A feasibility analysis on shale gas exploitation with supercritical carbon dioxide[J]. Energy Sources: Part A, 2012,34(15):1426-1435.
[2] 李根生,王海柱,沈忠厚,等.超临界CO2射流在石油工程中应用研究与前景展望[J].中国石油大学学报(自然科学版),2013,37(5):76-80, 87.
LI Gensheng, WANG Haizhu, SHEN Zhonghou, et al. Application investigations and prospects of supercritical carbon dioxide jet in petroleum engineering[J].Journal of China University of Petroleum(Edition of Natural Science), 2013,37(5):76-80,87.
[3] 孙宝江,孙文超.超临界CO2增黏机制研究进展及展望[J].中国石油大学学报(自然科学版),2015,39(3):76-83.
SUN Baojiang, SUN Wenchao. Research progress and prospectives of supercritical CO2thickening technology[J]. Journal of China University of Petroleum(Edition of Natural Science), 2015,39(3):76-83.
[4] MIDDLETON R S, CAREY J W, CURRIER R P, et al. Shale gas and non-aqueous fracturing fluids: opportunities and challenges for supercritical CO2[J]. Applied Energy, 2015,147:500-509.
[5] YOST A B I, MAZZA R L, REMINGTON R E I. Analysis of production response to CO2/sand fracturing: a case study[R]. SPE 29191-MS, 1994.
[6] CHEN Y, NAGAYA Y, ISHIDA T. Observations of fractures induced by hydraulic fracturing in anisotropic granite[J]. Rock Mechanics and Rock Engineering, 2015,48(4):1455-1461.
[7] 程宇雄,李根生,王海柱,等.超临界二氧化碳喷射压裂孔内流场特性[J].中国石油大学学报(自然科学版),2014,38(4):81-86.
CHENG Yuxiong, LI Gensheng, WANG Haizhu, et al. Flow field character in cavity during supercritical carbon dioxide jet fracturing[J]. Journal of China University of Petroleum(Edition of Natural Science), 2014,38(4):81-86.
[8] RAMEY H J. Wellbore heat transmission[J]. Journal of Petroleum Technology, 1962,14(4):427-435.
[9] HASAN A R, KABIR C S. Aspects of wellbore heat transfer during two-phase flow[J]. SPE Production & Facilities, 1994,9(3):211-216.
[10] KABIR C S, HASAN A R, KOUBA G E, et al. Determining circulating fluid temperature in drilling, work over, and well control operations[J]. SPE Drilling & Completion, 1996,11(2):74-79.
[11] HAGOORT J. Rameys wellbore heat transmission revisited[J]. SPE Journal, 2004, 9 (4):465-474.
[12] SPINDLER R. Analytical models for wellbore-temperature distribution[J]. SPE Journal, 2011,16(1):125-133.
[13] RAYMOND L R. Temperature distribution in a circulating drilling fluid[J]. Journal of Petroleum Technology, 1969,21(3):333-341.
[14] EICKMEIER J, ERSOY D, RAMEY H, et al. Wellbore temperatures and heat losses during production or injection operations[J]. Journal of Canadian Petroleum Technology, 1970,9(2):115-121.
[15] YOSHIOKA K, ZHU D, HILL A D, et al. Interpretation of temperature and pressure profiles measured in multilateral wells equipped with intelligent completions[R]. SPE 94097-MS,2005.
[16] 王海柱,沈忠厚,李根生.超临界CO2钻井井筒压力温度耦合计算[J].石油勘探与开发,2011,38(1):97-102.
WANG Haizhu, SHEN Zhonghou, LI Gensheng. Wellbore temperature and pressure coupling calculation of drilling with supercritical carbon dioxide[J]. Petroleum Exploration & Development, 2011,38(1):97-102.
[17] 王瑞和,倪红坚.二氧化碳连续管井筒流动传热规律研究[J].中国石油大学学报(自然科学版),2013,37(5):65-70.
WANG Ruihe, NI Hongjian. Wellbore heat transfer law of carbon dioxide coiled tubing drilling[J]. Journal of China University of Petroleum(Edition of Natural Science), 2013,37(5):65-70.
[18] 郭建春,曾冀,张然,等.井筒注二氧化碳双重非稳态耦合模型[J].石油学报,2015,36(8):976-982.
GUO Jianchun, ZENG Ji, ZHANG Ran, et al. A dual transient coupling model for wellbore of carbon dioxide injection well[J]. Acta Petrolei Sinica, 2015,36(8):976-982.
[19] SPAN R, WAGNER W. A new equation of state for carbon dioxide covering the fluid region from the triple-toint temperature to 1 100 K at pressures up to 800 MPa[J]. Journal of Physical and Chemical Reference Data, 1996,25(6):1509-1596.
[20] VESOVIC V, WAKEHAM W A, OLCHOWY G A, et al. The transport properties of carbon dioxide[J]. Journal of Physical and Chemical Reference Data, 1990,19(3):763-808.
[21] FENGHOUR A, WAKEHAM W A, VESOVIC V. The viscosity of carbon dioxide[J]. Journal of Physical and Chemical Reference Date, 1998,27:31-44.
[22] 汪志明,崔海清,何光渝.流体力学[M],北京:石油工业出版社,2006.
[23] WANG Z, SUN B, WANG J, et al. Experimental study on the friction coefficient of supercritical carbon dioxide in pipes[J]. International Journal of Greenhouse Gas Control, 2014,25:151-161.
[24] LIAO S M, ZHAO T S. An experimental investigation of convection heat transfer to supercritical carbon dioxide in miniature tubes[J]. International Journal of Heat and Mass Transfer, 2002,45(25):5025-5034.
[25] DROPKIN D, SOMERSCALES E. Heat transfer by natural convection in liquids confined by two parallel plates which are inclined at various angles with respect to the horizontal[J]. Journal of Heat Transfer, 1965,87(1):77-82.
[26] PETERSEN J, BJØRKEVOLL K S, LEKVAM K, et al. Computing the danger of hydrate formation using a modified dynamic kick simulator[R]. SPE/IADC, 2001.
[27] 张勇,唐人选.CO2井筒压力温度的分布[J].海洋石油,2007,27(2):59-64.
ZHANG Yong, TANG Renxuan. Study of distribution of wellbore pressure and temperature of CO2injection well[J]. Offshore Oil, 2007,27(2):59-64.

