轨道非线性能量阱阻尼对其减振性能的影响

王菁菁， 浩文明， 吕西林

(1.湖南工业大学 土木工程学院，湖南 株洲 412000； 2.同济大学 土木工程防灾国家重点实验室，上海 200092)

结构控制技术通过对主体结构施加被动或主动的作用力，改变结构主体的刚度或阻尼等，以达到减小能量输入和加速能量消耗的目的。其中，被动结构控制技术，由于不需要额外能量输入，概念简单，被成功应用于大量实际工程之中。调谐质量阻尼器(Tuned Mass Damper，TMD)是最为常见的被动控制方法，一般放置在建筑结构顶层，当TMD频率调至与主体结构相近时，可通过反向共振减小结构响应[1-3]。但传统TMD为线性阻尼器，刚度为定值，即只有一个自振频率。当原结构的频率由于结构受损、沉降或其他因素发生变化时，TMD减振性能退化，有时甚至放大主体结构的响应[4]。为解决这一问题，有学者提出了非线性的结构控制方法—非线性能量阱(Nonlinear Energy Sink，NES)[5]。从构成元素上看，NES与TMD十分相似，均是附加质量通过弹簧单元和阻尼单元与主体结构相连。但与TMD不同的是，NES中弹簧为非线性弹簧，产生本质非线性的回复力(即回复力中不包含线性成分且不可线性化)。现有NES的力-位移关系呈三次方函数关系，与TMD线性的力-位移关系进行类比，当输入能量(位移)不同时，NES线性化刚度不同。这使得NES能够与较广泛的频率发生共振，一方面使能量从主体结构单向传递至NES(即靶能量传递)，一方面耦合主体结构的不同模态，使能量从低阶模态传递至耗能更快的高阶模态[6-8]。

本文所研究的轨道非线性能量阱(Track Nonlinear Energy Sink，轨道NES)是一种新型的NES，由轨道和附加质量组成，通过轨道形状实现非线性回复力。轨道与主体结构固定，质量块沿轨道运动。本文将推导轨道NES的回复力表达式、轨道NES系统运动方程，并通过数值模拟考察两自由度主体结构附加轨道NES的响应。由于轨道NES减振性能对输入能量大小较敏感，本文又研究了轨道NES阻尼对其减振性能的影响。结果表明，通过调整轨道NES阻尼，可以有效改善轨道NES的刚度鲁棒性和能量鲁棒性。

1 轨道非线性能量阱

轨道NES通过质量块沿特殊设计的轨道运动产生非线性回复力，其物理模型可借由带轮小车沿轨道运动表示(见图1)。假设质量块不发生转动且与轨道保持接触，则轨道NES的自由体受力图可表示为图2。其中，mN为NES质量，uN和vN分别为NES相对于轨道的水平位移和竖向位移，z为轨道的水平位移，h(uN)为轨道的形状函数，和vN相等，可以通过uN表示。FNomal是NES作用在轨道上的法向反力，θ为轨道切线角度，可通过对轨道形状函数h(uN)求导得到，g为重力加速度。

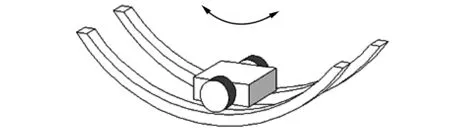
图1 轨道NES示意图Fig.1 Configuration of track NES

轨道NES的运动方程可以用拉格朗日方法得到[9]

(1)

其中，轨道NES的动能为

(2)

且有

vN=h(uN)

(3)

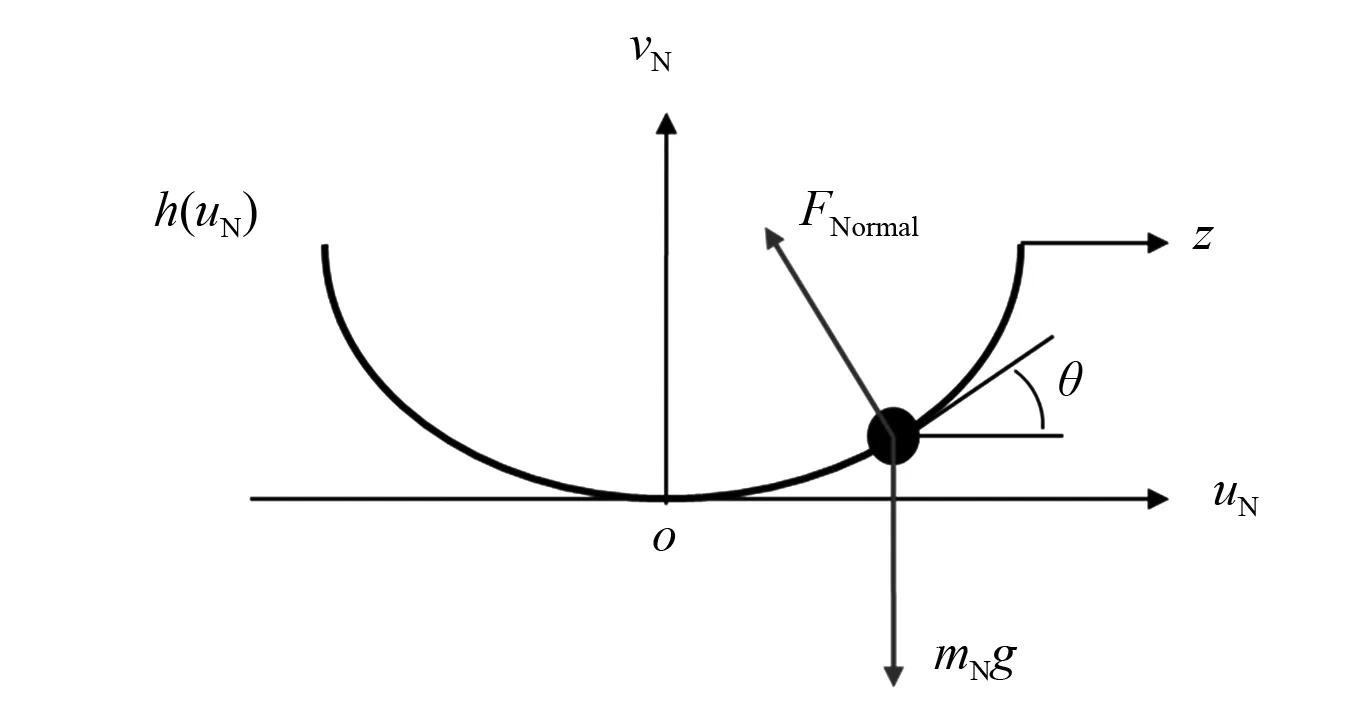
图2 轨道NES自由体受力图Fig.2 Free body diagram of track NES

轨道NES的势能为

V=mNgh(uN)

(4)

此处暂不考虑轨道NES阻尼，对式(2)和式(4)求偏导并展开，可得

(5)

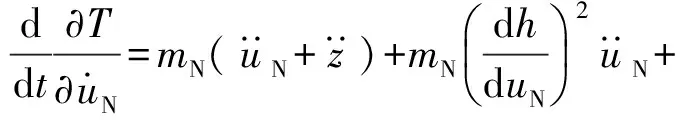
(6)

(7)

(8)

将以上各展开项带入拉格朗日方程，可得NES的运动方程

(9)

除去运动方程中惯性力项和轨道加速度作用的外力项，可求得轨道NES的回复力表达式为

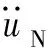
(10)

由该表达式可知，轨道NES的回复力与质量块的运动状态、轨道形状和形状函数的导数等有关，较以往NES的三次方回复力-位移关系更复杂，且轨道NES在同一位移处可能产生不同的回复力。这些特点使得轨道NES能够产生较以往NES更强的非线性回复力。

2 系统运动方程

将轨道NES置于一n个自由度的主体结构末端。主体结构为楼房结构模型，即各楼层质量通过刚度单元和阻尼单元串联，顶层质量通过非线性刚度单元(轨道)和阻尼单元与轨道NES连接(见图3)。在这里，轨道NES的阻尼简化为黏滞阻尼，用以模拟可能存在的材料阻尼和摩擦阻尼等。

图3 轨道NES系统模型示意图Fig.3 Phenomenological Model of track NES system

图3中，mi为第i个自由度的质量，ki为第i个质量的对应弹簧刚度，ci为第i个质量的对应黏滞阻尼系数，xi为第i个质量相对地面的位移，cN为轨道NES黏滞阻尼系数，xg为地面位移，其他符号含义与图2相同。同样，采用拉格朗日方法，系统中的总动能为

(11)

系统中的总势能为

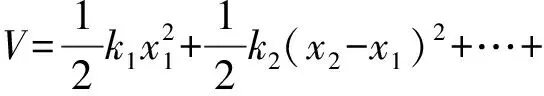
(12)

非保守力所做虚功为

(13)

分别对总动能、总势能和总虚功表达式求x1,x2, …,xn和uN的偏导可以得到该系统的运动方程为

(14)

3 轨道NES的优化

本文以某两自由度主体结构为例，对轨道NES进行数值优化并讨论其减振性能。优化使用MATLAB计算软件，通过建立State-Space模型或采用Differential Equation Editor模块的Simulink模型进行模拟。优化采用了加权平均的全局搜索方法，考虑了主体结构刚度和输入能量大小的变化，可分为三步进行：①选定NES轨道形状函数和NES质量的取值范围。②对于任意一种NES轨道-NES质量的组合在MATLAB中进行响应模拟。荷载使用脉冲荷载，通过设定主体结构初始速度施加。改变主体结构刚度和输入能量大小，重复脉冲响应模拟，并对不同情况下的结构响应求加权平均值。③优化的目标为使轨道NES系统与锁住系统(即轨道NES与顶层无相对位移，与顶层锁住)位移响应(层间位移均方根)的比值达到最小。该层间位移比值可通过式(15)表示。

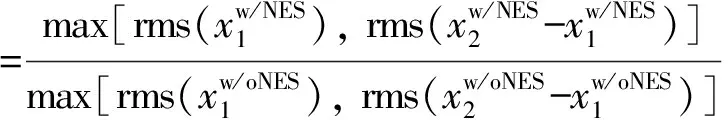
(15)

式中：上标w/NES为轨道NES参与减振控制；w/oNES为无轨道NES参与减振控制；rms为最小均方根；max为求最大值。

该主体结构第一、二层质量分别为24.3 kg和24.2 kg，楼层刚度分别为6 820 N/m和8 220 N/m，结构模态阻尼比为0.1%，结构固有频率分别为1.63 Hz和4.56 Hz。根据类似试验数据，轨道NES阻尼取为1.6 N·s/m。结构初始速度为0.15 m/s。

为了对比轨道NES和线性阻尼器TMD的减振效果，这里还对同一主体结构附加相同质量的TMD进行了优化，优化后的TMD弹簧刚度系数为210 N/m。

图4对比了轨道NES系统、TMD系统和锁住系统在初始速度为0.15 m/s时的顶层位移响应。经过优化的轨道NES和TMD减振效果明显，5 s内即可降低结构响应约60%。

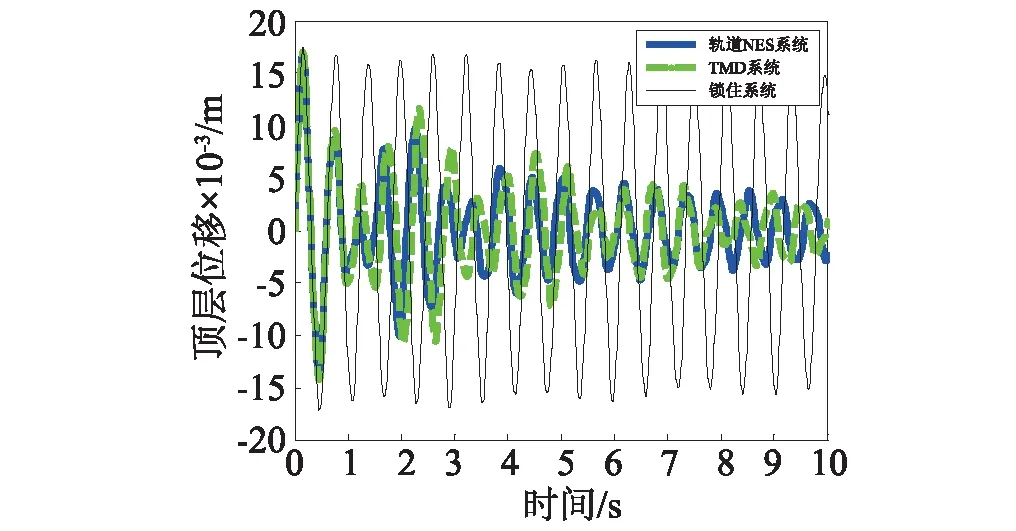
图4 0.15 m/s初始速度100%刚度的结构位移Fig.4 Displacements of 100% stiffness structures under 0.15 m/s initial velocity

图5中，考虑主体结构刚度退化，即主体结构刚度下降50%后对比各系统响应。由于TMD为线性阻尼器，仅能以单一频率参与工作，此时减振效果较图4下降明显。而轨道NES由于振动频率可变，减振效果依然十分明显，约10 s左右，结构响应已降至极小，能有效保护主体结构。轨道NES对刚度(频率)变化展现出优越的鲁棒性能。

图5 0.15 m/s初始速度50%刚度的结构位移Fig.5 Displacements of 50% stiffness structures under 0.15 m/s initial velocity

图6中，考虑增加初始速度至0.32 m/s，即增加系统的输入能量后对比各系统反应。TMD系统与锁住系统均为线性系统，输入能量大小的改变不影响两者的反应比例关系。但此时轨道NES的性能受到影响，这是由于轨道NES的频率特性随输入能量大小而变化，当初始速度偏离优化中采用的初始速度时，轨道NES不能保持最优的减振效果。为探索解决轨道NES对输入能量较敏感的问题，本文将重点考察轨道NES阻尼对其能量鲁棒性的影响。

为进一步说明轨道NES的频率特性随输入能量大小而变化，图7显示了轨道NES系统和锁住系统的加速度响应小波变换图。在约1.5 Hz和5 Hz处的能量曲线分别与主体结构的一阶和二阶频率相对应，阴影深浅表示能量大小，即颜色越深表示此处能量越大。观察可知，开始阶段能量较大，轨道NES系统中相当一部分能量通过高频运动(5～20 Hz)消耗，而随着系统中能量的减小，轨道NES的振动频率也发生变化。而锁住系统中，结构只在两基本频率处发生振动，且两频率处所分布能量的比值不随时间(能量减少)而改变。

图6 0.32 m/s初始速度100%刚度的结构位移Fig.6 Displacements of 100% stiffness structures under 0.32 m/s initial velocity

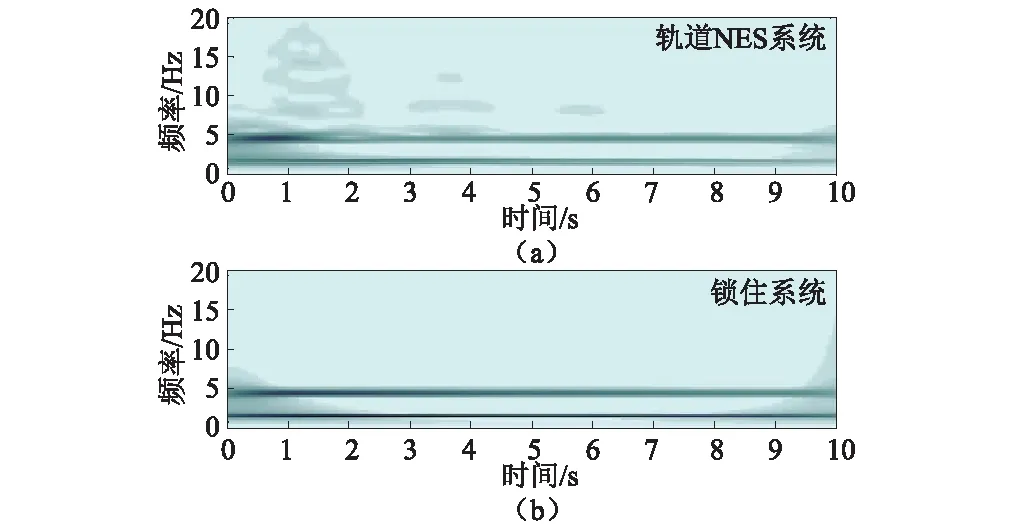
图7 轨道NES系统和锁住系统的加速度小波变换Fig.7 Wavelet transform of accelerations of the track NES and the locked systems

4 对轨道NES阻尼的讨论

为了全面考察轨道NES阻尼对其减振性能及对结构刚度和输入能量鲁棒性的影响，本文分别计算了初始速度为0.07 m/s、0.15 m/s和0.32 m/s时轨道NES系统与锁住系统的层间位移均方根比值。同时，在不同初始速度下，考察主体结构刚度的八种不同取值(为原始刚度的50%～120%)。各初始速度下轨道NES阻尼与层间位移比的关系见图8～图10。为了在图中更清晰地表达结果，图8～图10仅绘制了4种刚度下层间位移比。表1中列出了更为完整的结果。由图8～图10可知，当初始速度和结构刚度一定时，存在一个最优阻尼值使轨道NES的减振性能最佳，即可通过调整轨道NES阻尼改善其减振性能。

图8 0.07 m/s初始速度下的层间位移比Fig.8 Storey drift ratio at the initial velocity of 0.07 m/s

图9 0.15 m/s初始速度下的层间位移比Fig.9 Storey drift ratio at the initial velocity of 0.15 m/s

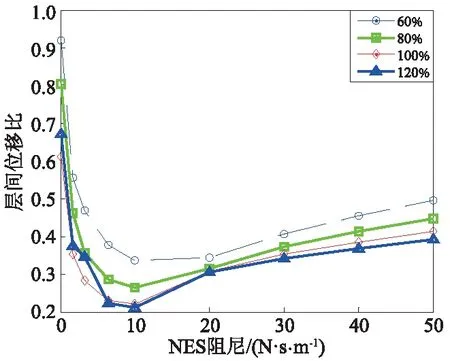
图10 0.32 m/s初始速度下的层间位移比Fig.10 Storey drift ratio at the initial velocity of 0.32 m/s

表1 不同初始速度和主体结构刚度组合下的最优阻尼

表1列出了不同初始速度和主体结构刚度组合时，对应最小层间位移比的轨道NES阻尼值。总体来说，与主体结构刚度相比，最优阻尼随初始速度变化产生的波动较大，这一点与轨道NES对输入能量较敏感的特点相符，同时说明将调整NES阻尼作为改善手段的可行性。在初始速度方面，以0.15 m/s为基准初始速度，当初始速度增大或减小时最优阻尼值均呈现增大趋势。在主体结构刚度方面，对于具备相当振动能量的系统，主体结构刚度较小时最优阻尼值较大，刚度较大时最优阻尼值较小。

图11对比了使用原阻尼值的轨道NES系统、使用最优阻尼值的轨道NES系统以及锁住系统在初始速度增至0.32 m/s的结构位移响应。由图可知，阻尼经过优化的轨道NES减振性能大为提高，仅3 s内位移降至锁住系统响应的20%。阻尼优化后轨道NES对输入能量发生变化结构的减振效果有显著提高。

图11 0.32 m/s初始速度阻尼优化前后的结构位移Fig.11 Displacements before and after the damping optimization under 0.32 m/s initial velocity

图12对比了使用原阻尼值的轨道NES系统、使用最优阻尼值的轨道NES系统以及锁住系统在主体结构刚度下降50%的结构位移响应。由图可知，阻尼优化后的轨道NES系统4 s内位移降至锁住系统反应的20%，优化阻尼对刚度发生变化结构的减振效果亦有显著提高。

图12 0.15 m/s初始速度50%刚度阻尼优化前后的结构位移Fig.12 Displacements of 50% stiffness structures before and after the damping optimization under 0.15 m/s initial velocity

由于轨道NES阻尼较其他参数(如轨道形状等)更容易调节，在未来的研究中，可考虑通过半主动方法或其他变阻尼方法控制轨道NES阻尼的变化，使轨道NES同时具备对频率和对输入能量的鲁棒性。

5 结 论

本文所研究的轨道NES是一种新型的非线性结构控制方法，通过附加质量沿特殊设计的轨道运动产生非线性回复力。与传统线性控制方法TMD相比，轨道NES在主体结构刚度发生变化时仍具有较好的减振性能，但同时，其减振性能受输入能量大小的影响较大。为进一步完善轨道NES，本文考察了轨道NES阻尼对其减振性能的影响。研究发现轨道NES的减振效率与其自身的阻尼有关，当输入能量大小与优化时输入能量偏离较大时，可以通过调节轨道NES阻尼使结构响应保持在较低水平。同时，调节轨道NES阻尼对刚度变化结构的减振性能亦有改善。研究可调节阻尼的轨道NES为开发同时具备输入频率鲁棒性和能量鲁棒性的非线性结构控制方法提供了可能。

致谢：

本文中对轨道非线性能量阱的研究得到了美国伊利诺伊大学香槟分校Billie F. Spencer, Jr.教授和田纳西大学Nicholas Wierschem教授的悉心指导和帮助。作者在此表示衷心感谢。作者在此表示衷心感谢。

[ 1 ] HOUSNER G W, BERGMAN L A, CAUGHEY T K, et al. Structural control: past, present, and future[J]. Journal of Engineering Mechanics, 1997,123 (9): 897-971.

[ 2 ] SPENCER B, NAGARAJAIAH S. State of the art of structural control[J]. Journal of Structural Engineering, 2003, 129(7): 845-856.

[ 3 ] WEBER F, FELTRIN G, HUTH O. Guidelines for structural control[R]. Structural Engineering Research Laboratory. Dubendorf: Swiss Federal Laboratories for Materials Testing and Research, 2006.

[ 4 ] SUN C, EASON R P, NAGARAJAIAH S， et al. Hardening düffing oscillator attenuation using a nonlinear TMD, a semi-active TMD and multiple TMD[J].Journal of Sound and Vibration, 2013, 332 (4): 674-686.

[ 5 ] VAKAKIS A F. Inducing passive nonlinear energy sinks in vibrating systems [J]. Journal of Vibration and Acoustics, 2001, 123(3): 324-332.

[ 6 ] MCFARLAND D M, BERGMAN L A, VAKAKIS A F. Experimental study of non-linear energy pumping occurring at a single fast frequency[J]. International Journal of Non-Linear Mechanics, 2005,40 (6): 891-899.

[ 7 ] NUCERA F, IACONO F L, MCFARLAND D M, et al. Application of broadband nonlinear targeted energy transfers for seismic mitigation of a shear frame: experimental results[J]. Journal of Sound & Vibration, 2008, 313(1/2): 57-76.

[ 8 ] NUCERA F, MCFARLAND D M, BERGMAN L A, et al. Application of broadbandn onlinear targeted energy transfers for seismic mitigation of a shear frame: computational results[J]. Journal of Sound & Vibration, 2010, 329(15): 2973-2994.

[ 9 ] CRAIG R R, KURDILA A J. Fundamentals of structural dynamics[M]. 2nd ed. Hoboken: Wiley, 2006.

[10] WANG J, WIERSCHEM N E, SPENCER B F, et al. Track nonlinear energy sink for rapid response reduction in building structures[J]. Journal of Engineering Mechanics, 2015, 141(1): 04014104.