悬索桥施工期大尺寸主缆驰振分析方法研究

李胜利, 王超群, 宁佐强, 王东炜

(郑州大学 土木工程学院，郑州 450001)

一般工程界所认为的驰振是细长物体因气流自激作用产生的一种纯弯曲大幅振动，理论上是发散的，即不稳定的[1]。但是人们在研究中发现，驰振现象应当是一种横风向运动占主导作用的三自由度运动[2]，主要发生在具有非流线型截面的细长钝体结构中。成桥后的主缆截面一般呈圆形，理论上不会发生驰振现象。然而施工期暂态主缆却并非圆形截面,在不同施工阶段截面形状各异,这使其有发生驰振失稳的可能性。主缆(见图1)一般由上百根索股组成,每根索 股又由上百根镀锌钢丝组成[3]。其中每根索股的制造可由厂家在工厂完成，但是由索股组装成主缆的工序却因主缆截面尺寸过大而必须在施工现场完成,而且单根索股的架设时间有随着主缆跨径的增加而有变长的趋势，如东海某大跨径悬索桥主缆单根索股架设需要5 h左右。随着索股架设工序的推进,暂态主缆的截面形状不断变化,主缆的驰振性能也在不断变化。由于主缆在架设过程中尚未承受吊索等的约束作用，故而暂态主缆若在风的作用下发生驰振现象，必然会有较大的振动幅度，严重影响了施工安全性和工人舒适性。这种情况下，停工是在所难免的，因此也严重影响了整个桥梁架设的施工进度，以东海某大跨径悬索桥(见图2)为例，其平均每天索股架设根数竟不到一根。因此进行悬索桥大尺寸主缆施工期驰振性能研究很有必要。研究表明，由传统单自由度驰振研究方法得到的临界风速及失稳风攻角范围均和实际观察到的数据有一定程度的出入[4]，这对有效预防暂态主缆驰振失稳现象的发生是不利的，故而有必要进一步改进驰振分析方法。

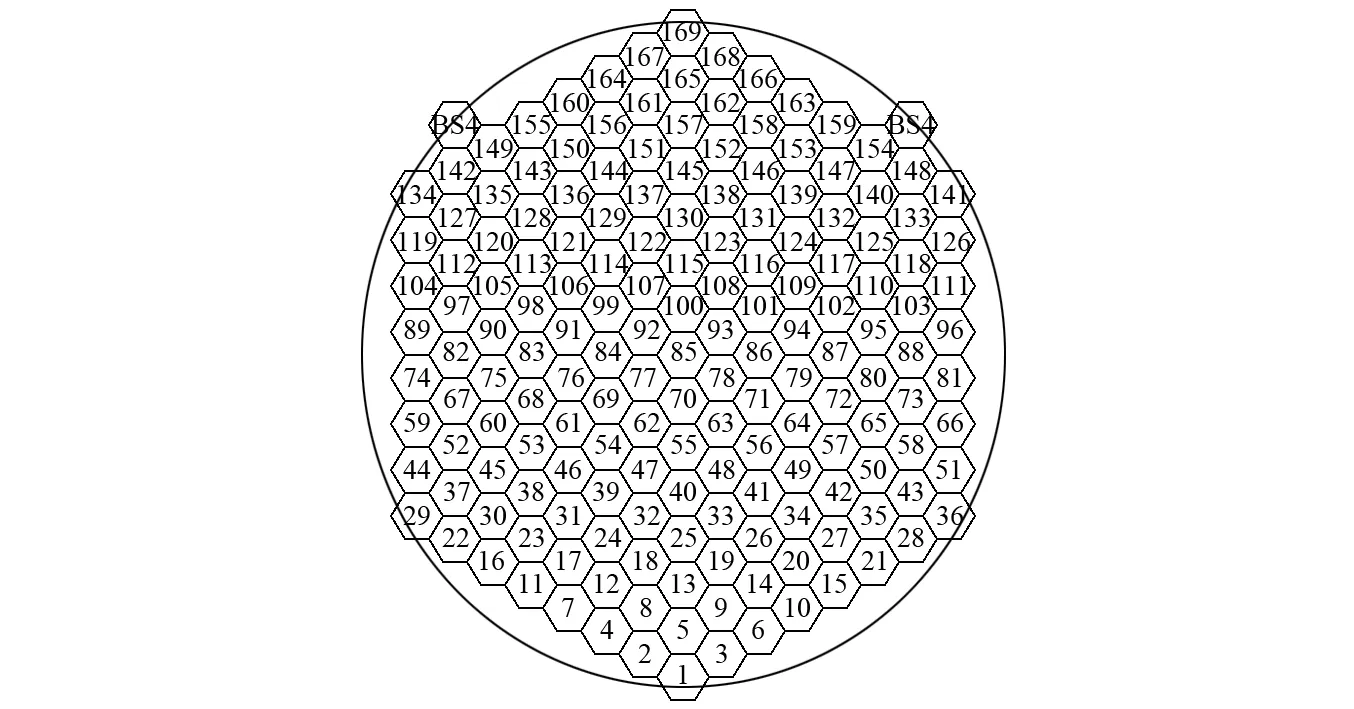
图1 主缆索股牵引形象进度图Fig.1 Visual progress chart of main cable strands

自DenHartog在其横风向驰振模型中，将结构横风向速度引入气动力项中，建立被广泛运用的单自由度驰振分析方法之后[5]，Nigol等[6]又在扭转驰振气动力模型中引入了结构的扭转，Yu等[7]则在竖向扭转两自由度驰振模型中同时考虑的结构横风向运动速度和结构扭转对相对风速的影响。国内的徐风云等[8]指出施工期强风作用下主缆具有三维振动特征，即横向、竖向和纵向复合振动，另外两根主缆三维振动具有不同步振动的特性等等；李胜利等则基于暂态主缆可能发生驰振失稳的理论，采用CFD 数值模拟和有限元数值计算的研究方法，分析得到了东海某大跨径悬索桥主缆施工期各工况可能发生驰振失稳的风攻角范围。

已有的研究多是基于单自由度驰振研究方法，即便涉及到主缆驰振的多自由度特征，也仅仅是定性的分析，未能定量的提出一个同时考虑暂态主缆不同方向运动及其相互影响作用的模型。基于此，本文建立了一个同时考虑暂态主缆横风向运动及顺风向运动的二自由度驰振模型，借用Routh-Hurwitz代数判据[9]推导得到了该模型下的临界失稳状态方程。基于东海某大跨径悬索桥的工程实例，运用本文推导的两自由度驰振分析模型，计算得出施工期主缆的驰振临界风速，并和登哈托准则进行对比分析。

图2 东海某大跨径悬索桥总体布置图Fig.2 General layout of the suspension bridge

1 悬索桥施工期暂态主缆驰振分析方法

按相对攻角变化所建立的气动自激力理论，忽略了物体周围非定常流场的存在，因而是将气流视为定常的，这种理论可以称之为准定常理论，相应的气动力则称为准定常力。实践证明，在静态条件下所得到的三分力系数随风攻角变化的曲线，已经足以作为建立驰振现象的理论基础，即驰振基本上是由准定常力控制的。传统的单自由度驰振模型以及本文即将提出的二自由度驰振模型均是以准定常理论为基础的。

1.1 单自由度驰振模型

假设均匀流以攻角α、速度Uα流过一个暂态主缆的的断面(见图3)。

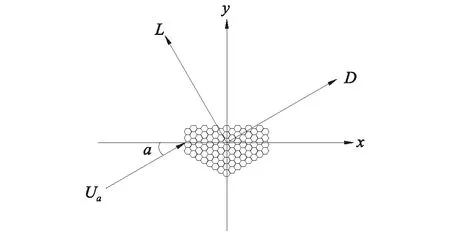
图3 缆索上的升力与阻力Fig.3 Lift and drag forces on main cable

图3中所示主缆断面的竖向振动方程可表示为

(1)

(2)

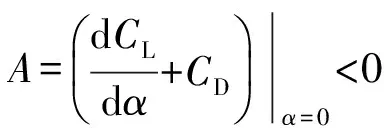
(3)

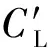
1.2 二自由度驰振模型

一般情况下，暂态主缆的驰振响应包括水平向(顺风向)、竖向(横风向)和扭转三个自由度的分量，但大多以横风向运动为主。因此在桥梁的抗风设计中一直沿用传统的单自由度DenHartog判据，这对小跨径的桥梁施工而言，计算精度已经达到工程实践的需求。李永乐等[12]在研究悬索桥施工期驰振时，发现多自由度分析方法较单自由度驰振模型能更真实地反映主缆的驰振性能。

仅就单根主缆而言，由于各根索股紧密排列，因而可认为扭矩引起的扭转偏量很小。本文暂且忽略因截面扭转引起的相对风速改变。可建立同时考虑主缆横风向和顺风向运动的气动力模型，如图4所示。

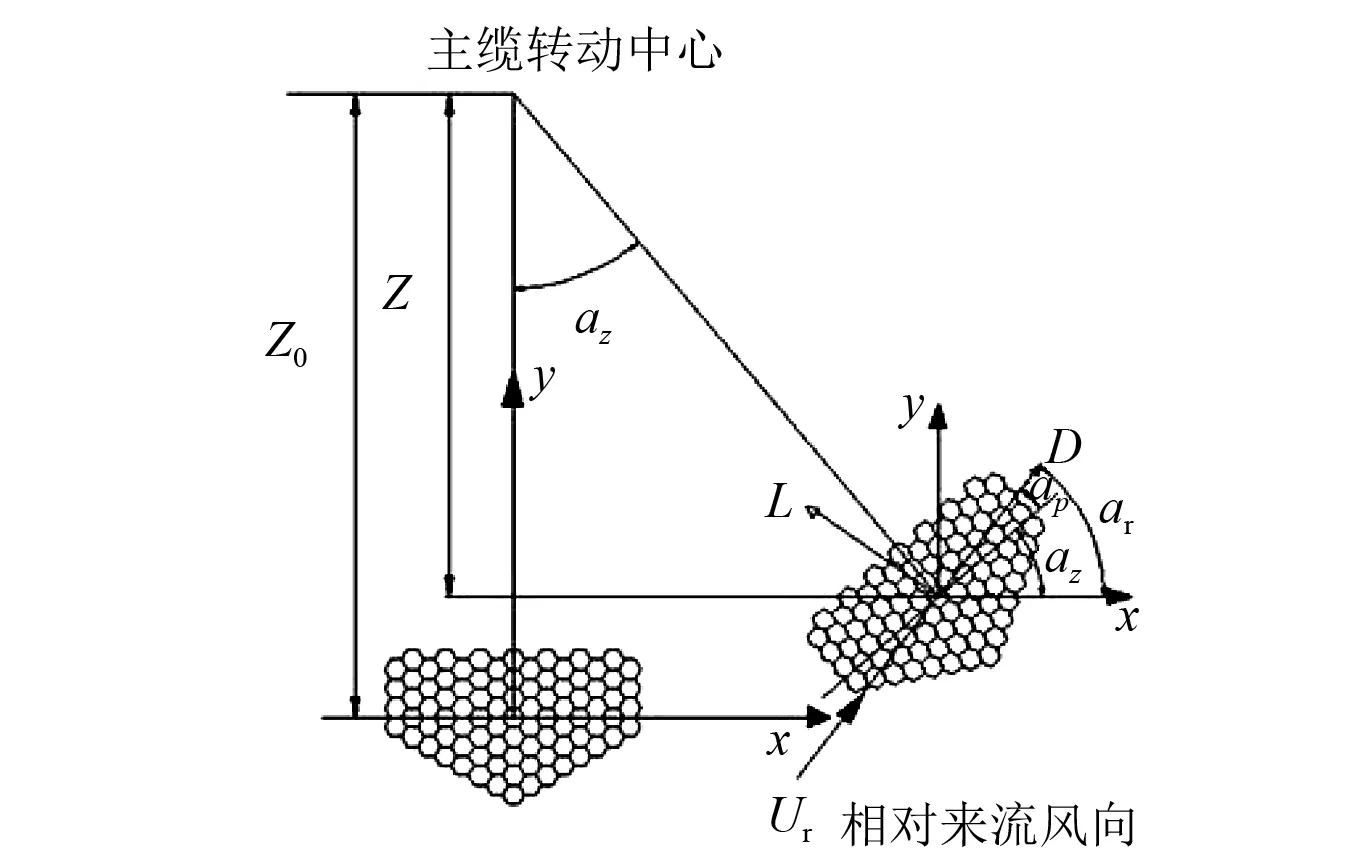
图4 暂态主缆二自由度驰振分析模型Fig.4 Two-degree-of-freedom model for galloping of main cable

x-o-y为体轴坐标系，L-O-D为风轴坐标系。相对风速及风攻角之间的关系可表示为[13]

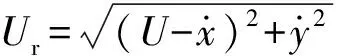
(4)

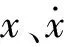
在风轴坐标系下，阻力及升力可分别表示为

根据几何关系，将其转换为体轴坐标系下的阻力及升力，转换关系为

Fx=FDcos(αr)-FLsin(αr)
Fy=FDsin(αr)+FLcos(αr)

(5)

式中：α=α0+αr为总的风攻角；α0为初始风攻角；CD(α)和CL(α)为阻力系数和升力系数；ρ为主缆所在处的空气密度；D为主缆的特征宽度(取迎风面宽度，即截面的高度)；Fx、Fy分别为体轴坐标系下的水平力和竖向力。

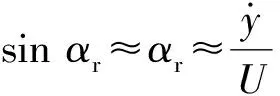
(6)

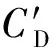
由结构动力学[14]知识可知，暂态主缆两自由度运动方程可表示为

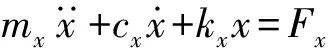
(7)

式中：mx、my分别为x、y方向的系统单位质量；cx、cy分别为x、y方向的系统阻尼；kx、ky分别为x、y方向的系统刚度。

将式(6)代入式(7)中，可得

(8)

式(8)可合并同类项，整理之后简化为

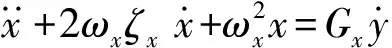
(9)

其中，

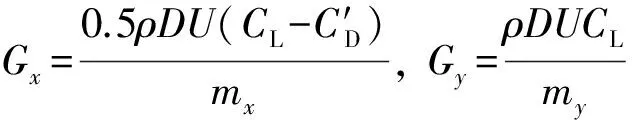
(10)

显而易见，式(10)中，耦合因子Gx、Gy、Gz很难同时为零。根据文献[13]可初步判断，同覆冰导线一样，暂态主缆一旦发生驰振，必然会有水平竖向耦合现象的发生。

下面建立微分方程式(9)对应的特征方程

假设x(t)=Xest，y(t)=Yest则式(10)可化为

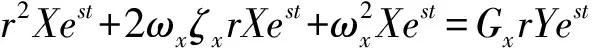
(11)

约去公因子est，可得

(12a)

(12b)

s4+2(ωxζx+ωyζy)s3+(ωx+ωy+4ωxωyζxζy+GxGy)s2

(13)

像式(9)这种解耦困难的复杂多自由度体系运动方程可借助代数判据来判断系统的运动稳定性，本文采用Routh-Hurwitz判据，其本质反映了特征方程系数与其特征根之间的关系。

式(13)所对应的胡尔维茨矩阵为

(14)

其中，

H4=1,H3=2(ωxζx+ωyζy),

(15)

系统稳定的充要条件为Δi>0，i=0, 1, 2, 3。

其中，Δi为胡尔维茨系数矩阵D的各阶主子行列式值，即

(16)

展开后，可得

Δ1=H3=2(ωxζx+ωyζy),

(ωxζx+ωyζy)(8ωxωyζxζy+2GxGy)-GxGz,

(ωxζx+ωyζy)(8ωxωyζxζy+2GxGy)-GxGz)×

(ωxζx+ωyζy)(8ωxωyζxζy+2GxGy)-GxGz)×

(17)

式中：ωx、ωy分别为x、y方向的结构圆频率，ωx=2πfx、ωy=2πfy；fy、fx则分别为结构两个振动方向的自振频率，可通过建立有限元模型进行动力特性分析得到；ζx、ζy为两个方向的结构阻尼比，本文中取一般值1%[15]。

根据文献[13], 通过求解Δi=0临界状态方程便可以得到暂态主缆系统的驰振临界风速。

2 工程实例分析

本文以东海某大跨径悬索桥施工期主缆为工程实例分析对象，选取其中四个典型工况(见图5),这四种典型工况可分别代表主缆施工过程中的下部三角形截面工况、中部五边形截面工况以及顶部尖顶型截面工况。

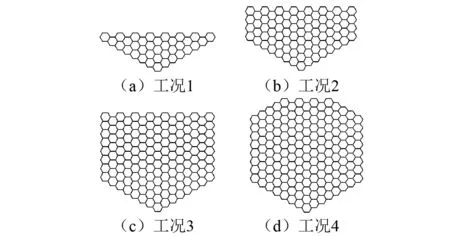
图5 施工期主缆四种典型工况截面Fig.5 Different working conditions of transient main cables during construction

2.1 驰振力系数的数值计算

考虑到实际风洞试验周期长、设备要求高等缺点，本文采用计算流体软件Fluent计算四种典型工况主缆在风攻角-5°～+5°内的气动力系数。数值模型考虑猫道对暂态主缆的影响，具体计算设置与文献[16]一致。计算得到四种典型工况下对应不同风攻角的阻力、升力系数变化曲线如图6～图9所示。

由DenHartog判据可知，驰振力系数A<0是系统运动不稳定的必要条件，如此可初步推断表1中出现负值的工况、风攻角组合下，有可能发生驰振失稳现象。

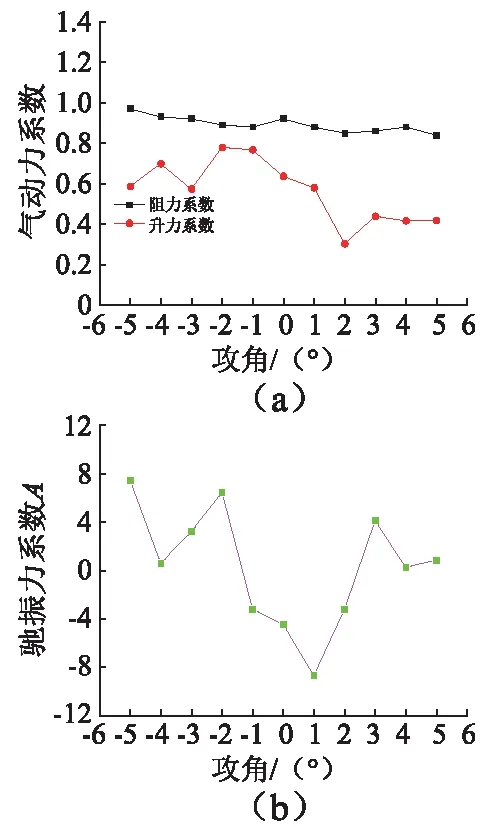
图6 工况1的升力系数、阻力系数及驰振力系数Fig.6 The lift, drag, and galloping coefficients of case 1

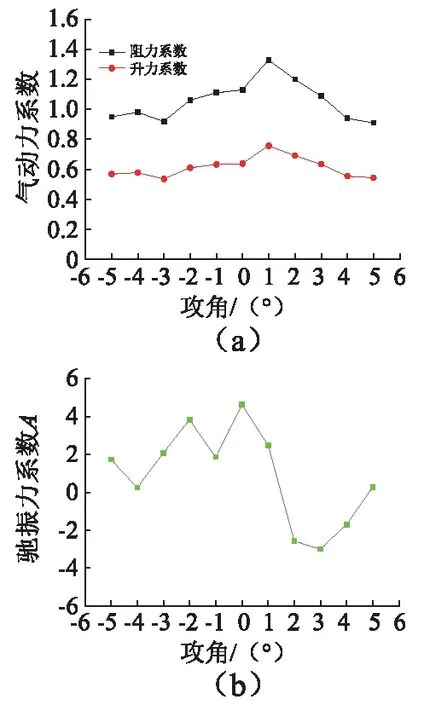
图7 工况2的升力系数、阻力系数及驰振力系数Fig.7 The lift, drag, and galloping coefficients of case 2

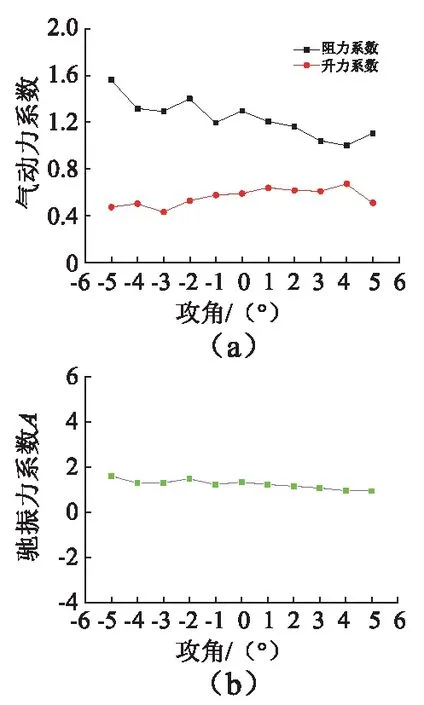
图8 工况3的升力系数、阻力系数及驰振力系数Fig.8 The lift, drag, and galloping coefficients of case 3

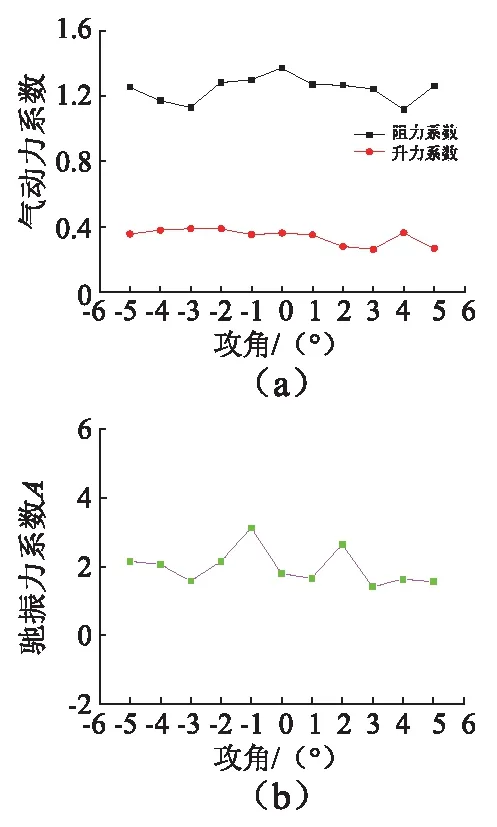
图9 工况4的升力系数、阻力系数及驰振力系数Fig.9 The lift, drag, and galloping coefficients of case 4

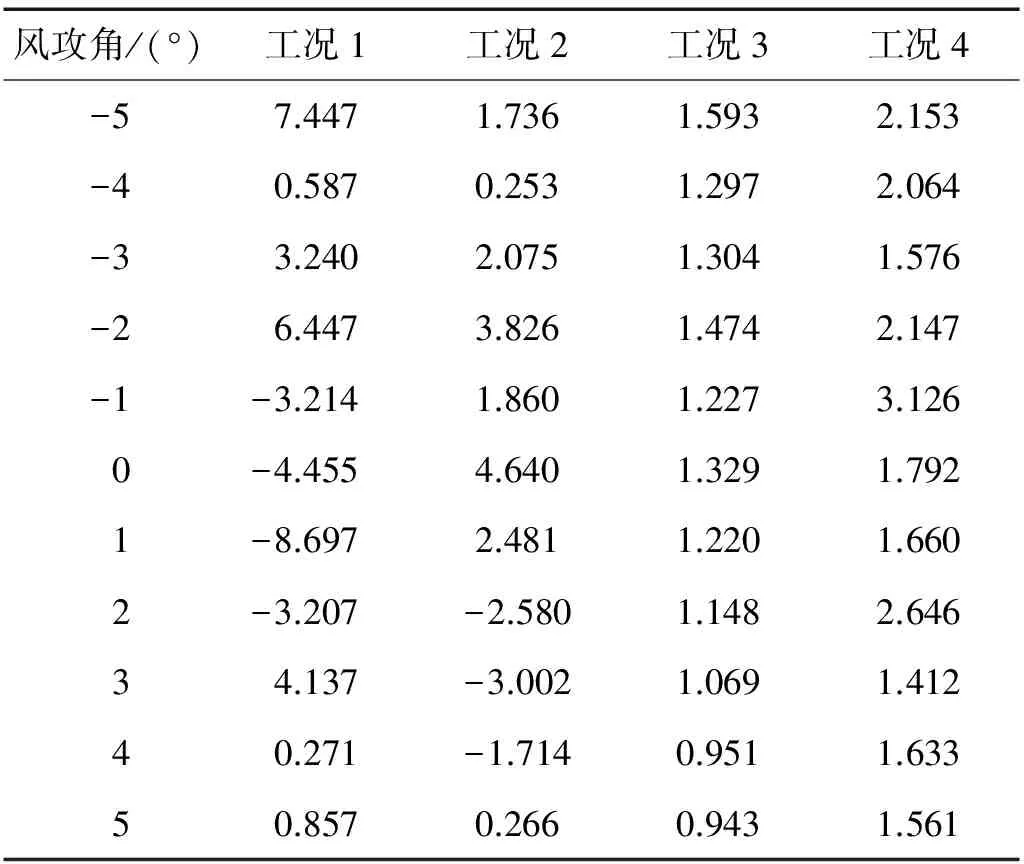
表1 暂态主缆各工况不同风攻角情况下的驰振力系数

2.2 暂态主缆动力特性有限元计算

采用ANSYS建立东海某大跨径悬索桥桥塔、猫道及主缆的有限元模型(见图10)。考虑预应力的影响，提取各典型工况前10阶自振频率及振型如表2所示。

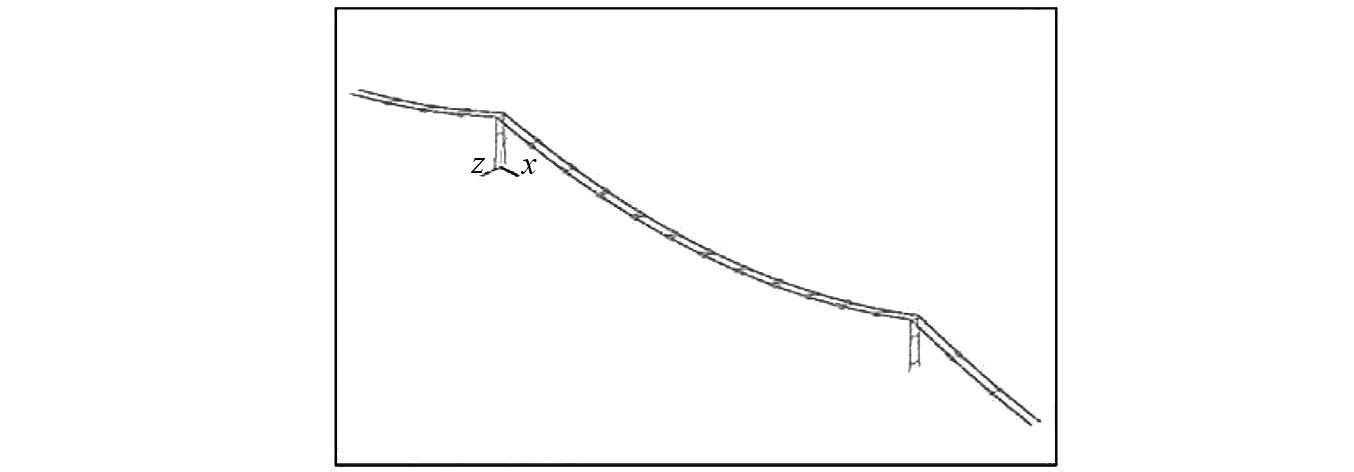
图10 东海某大跨径悬索桥施工期有限元模型Fig.10 Finite element model of the suspension bridge during construction

表2 暂态主缆各工况不同风攻角情况下的驰振力系数

2.3 两种模型下驰振临界风速对比分析

由表1可知，工况1下可能发生驰振失稳的风攻角范围为-1°～2°，工况2下可能发生驰振失稳的风攻角范围为2°～4°，工况3、工况4由于为主缆施工后期工况，没有出现驰振力系数小于零的情况。为了方便比较，不妨将上述可能发生失稳的情况列为六组组合，如表3所示。

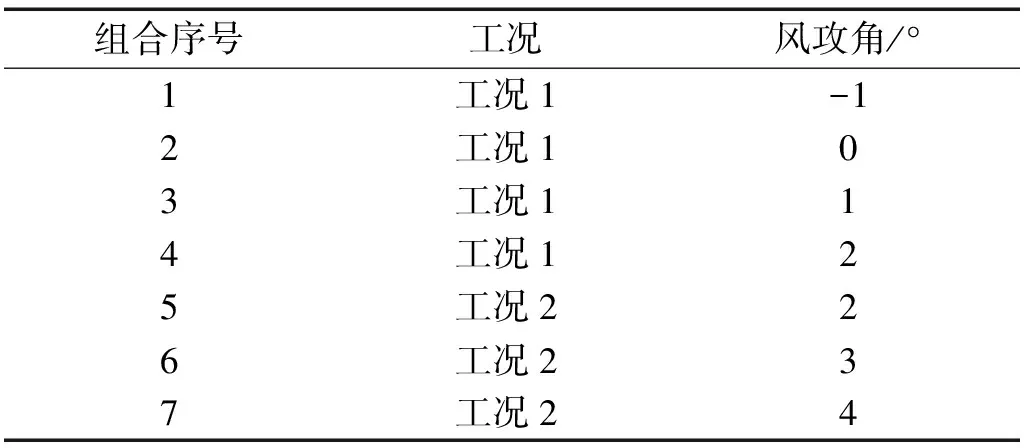
表3 可能发生驰振失稳的工况、风攻角组合

本文选取(f1，f3)及(f2, f4)两种模态组合的自振频率作为二自由度驰振模型的计算频率；单自由度驰振模型则可取各工况的第一阶横风向(竖向)自振频率f3作为计算频率；主缆阻尼比ζ可根据相关经验取为1%；各工况主缆单位长度质量m分别为：862.79 kg/m、1 941.28 kg/m；；特征宽度D分别为：0.25 m、0.42 m。分别运用传统单自由度模型和两种不同模态组合下的二自由度驰振模型计算表3中所给的六种可能发生驰振失稳情况下的驰振临界风速。由于采用二自由度驰振模型计算驰振临界风速时需要用到Routh-Hurwitz判据，计算过程较为复杂且容易出错，现以1号组合为例，取(f1，f3)模态组合简要介绍一下其计算过程。表4为Routh-Hurwitz判据所需的计算参数。

表4 计算参数

将表4中的H0,H1,H2,H3及H4代入Hurwitz系数矩阵，可得出该系数矩阵的各阶主子行列式

Δ1=H3=0.017 379 667；

Δ2=H3H2-H1H4=0.004 287 536+0.017 379 667×

(-1.745 58E-010×U2)-1.759 18E-009×U3；

Δ3=H1(H3H2-H1H4)=1.263 05E-005+

5.11 981E-005GxGy+0.001 341 674GxGz+

0.017 379 667×GxGz×GxGy-GxGzGxGz；

Δ4=H0×Δ3

(18)

由上文可知，系统稳定的充要条件为

Δi>0,i=0, 1, 2, 3, …,

因此只需分别令Δ1,Δ2,Δ3和Δ4等于零，即可解得驰振临界风速Ug。

由于H0H3均为常数，只需以下两式成立

H1=0.002 9+1.759 2E-009×U3=0

(19)

H3H2-H1H4=0.004 287 54+0.017 379 67×

(-1.745 58E-010×U2)-1.759 18E-009×U3

(20)

解得Ug=U=134.58 m/s。

表5为所有组合采用单自由度模型和两自由度模型计算所得的驰振临界风速。

由表5可知，两自由度模型计算方法分别采用两种不同振型组合的计算结果差别很小，这是因为两种振型组合的自振频率十分接近，由此可以预见采用前四阶振型f1,f2，f3,f4所对应的四种振型组合(f1,f2)、(f1,f3)、(f2,f3)和(f2,f4)所得的驰振临界风速差别很小，因此下面只取两自由度模型的振型组合(f1,f3)对应的计算结果与单自由度模型的计算结果进行对比分析，图11为两种计算方法所得临界风速。

表5 两种计算模型计算结果

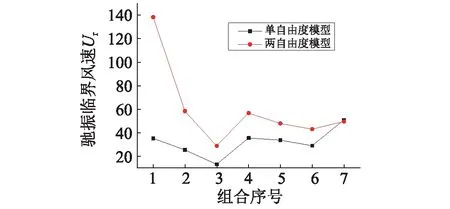
图11 两种驰振模型计算所得驰振临界风速对比Fig.11 The galloping critical wind speed calculated by the two models

由图11可知，对于可能发生驰振的七组工况，其中六组用本文介绍的两自由度计算方法比用传统单自由度方法计算所得的驰振临界风速高。即两自由度分析方法分析所得相同风速下主缆发生驰振的可能性更小，更加安全。

对比两种分析方法，Den Hartog单自由度驰振理论只考虑质点横风向的上下振动，不考虑横桥向的振动，与实际观察到的主缆驰振现象有一定差异；本文两自由度驰振分析方法和文献[13]关于覆冰导线的两自由度驰振分析类似，考虑了竖向和横桥向多种模态的耦合振动。研究者在不考虑猫道气动干扰效应的主缆驰振时域分析中，也指出多自由度分析方法更加贴近现实情况，较单自由度驰振模型能更真实地反映主缆的驰振性能。因此，用传统单自由度方法分析主缆驰振时所得结论偏不安全，可能对是否发生驰振产生误判。

3 结 论

(1)基于本文提出的主缆驰振两自由度分析方法，取主缆前四阶振型，共有四组两自由度振型组合，对四组振型组合分别计算所得四组驰振临界风速差别很小。

(2)由于多自由度分析方法更为接近实际情况，较单自由度驰振模型能更真实地反映主缆的驰振性能，其计算结果可信度更高。

(3)两自由度分析方法比传统单自由度计算方法所得驰振临界风速大，传统单自由度方法对主缆的驰振分析存在误判的可能性。

[ 1 ] 陈政清. 桥梁风工程[M]. 北京：人民交通出版社，2005: 66-68.

[ 2 ] GJELSTRUP H, GEORGAKIS C T. A quasi-steady 3 degree-of-freedom model for the determination of the onset of bluff body galloping instability[J]. Journal of Fluids and Structures, 2011, 27(7): 1021-1034.

[ 3 ] 李胜利，欧进萍. 大跨径悬索桥施工期暂态主缆驰振分析[J]. 土木工程学报,2009,42(9): 74-81.

LI Shengli, OU Jinping. Galloping analysis for the transient main cable of long-span suspension bridges during construction[J]. Journal of Highway and Transportation Research and Development, 2009, 42(9): 74-81.

[ 4 ] TETSURO T, ITOH Y. Unstable aerodynamic phenomena of a rectangular cylinder with critical section[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 83(1): 121-133.

[ 5 ] DEN HARTOG J P. Transmission line vibration due to sleet[J]. American Institute of Electrical Engineers, 1932, 51(4): 1074-1081.

[ 6 ] NIGOL O, BUCHAN P G. Conductor galloping Part I: den hartog mechanism[J]. IEEE Transactions on Power Apparatus and Systems, 1981, 100(2): 699-707.

[ 7 ] YU P, DESAI Y M, SHAH A H. Three-degree-of freedom model for galloping. Part I: formulation[J]. Journal of Engineering Mechanics, 1993, 119(12): 2404-2425.

[ 8 ] 徐风云，陈德荣. 2007年台风多发期架设西堠门大桥钢箱梁的可行性研究[R]. 舟山： 浙江省舟山连岛工程建设指挥部，2006.

[ 9 ] 刘延柱. 高等动力学[M]. 北京：高等教育出版社，2000.

[10] ALONSO G, MESEGUER J. A parametric study of the galloping stability of two-dimensional triangular cross-section bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94(4): 241-253.

[11] ALONSO G, MESEGUER J, PEREZ-GRANDE I. Galloping stability of triangular cross-sectional bodies: a systematic approach[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(9/10/11): 928-940.

[12] 李永乐, 易仁彦, 王东绪, 等. 悬索桥主缆架设过程驰振性能时域分析[J]. 西南交通大学学报, 2013, 48(1): 21-28.

LI Yongle,YI Renyan,WANG Dongxu, et al. Time-domain analysis of galloping of main cables of suspension bridge during erection process[J]. Journal of Southwest Jiaotong University, 2013, 48(1): 21-28.

[13] 马文勇, 顾明. 考虑摆动效应的覆冰导线两自由度驰振稳定性分析[J]. 工程力学,2012,29(1): 195-201.

MA Wenyong, GU Ming. Galloping instability of two degree of freedom of iced conductor with swing[J]. Engineering Mechanics, 2012,29(1): 195-201.

[14] 克拉夫 R，彭津 J. 结构动力学[M]. 王光远， 译. 北京： 高等教育出版社， 2006: 17-20.

[15] 中华人民共和国交通部. 公路桥梁抗风设计规范： JTG/T D-60-01—2004[S]. 北京： 人民交通出版社， 2004.

[16] 李胜利, 王超群, 王东炜, 等. 大跨径悬索桥施工期尖顶型主缆驰振性能分析[J]. 振动与冲击, 2015, 34(22): 154-160.

LI Shengli, WANG Chaoqun, WANG Dongwei, et al. Galloping performance of large scale spire type main cable of suspension bridge during construction[J]. Journal of Vibration and Shock, 2015, 34(22): 154-160.