风攻角对某大跨斜拉桥气动系数影响研究
孙开旗,肖玉德
(安徽交通职业技术学院,安徽 合肥 230051)
0 引言
静三分力系数是在桥梁抗风领域中最基本的无量纲气动参数,用于表征桥梁风荷载,是桥梁静风荷载驰振响应分析、抖振响应分析和稳定性分析的基础。
本文以计算流体力学为基础,用相关软件对斜拉桥主梁截面周围的静力流动进行了数值模拟,研究风在不同攻角下对静三分力系数和Storohar 的影响,得出风攻角对本桥主梁气动特性的影响规律,进而对实际工程起到指导、借鉴作用[1]。
1 气动系数
1.1 静风三分力系数
静风三分力和静风三分法力系数表示如式(1)至式(3)所示。

式 中:FD——阻 力;FL——升 力;MT——扭 转 力 矩;CD——阻力系数;CL——升力系数;CM——扭转力矩系数;ρ——空气密度;U——来流风速;D——主梁特征高度;B——主梁特征宽度。
1.2 Storohar 数
流体流过桥梁结构后通常会产生旋涡脱落现象,这是引起桥梁结构涡激振动的主要原因。Storohar 数计算如式(4)所示。

式中:St——Storohar 数;f——涡脱频率;H——结构特征尺度(桥梁截面高度);U——来流速度。
2 工程实例
2.1 基本概况
本文以某斜拉桥为研究背景,主桥跨径布置(150+320+150)m,全长620m,为双塔三跨双索面半漂浮体系斜拉桥,主塔采用双“子”式混凝土桥塔。主梁中心处梁高3.2m,顶面宽31.0m,底面宽31.2m。本文研究风攻角对横隔梁处断面气动系数影响。
2.2 计算域与网格划分
计算模型的尺寸采用实际尺寸。经参考相关文献和数次尝试,计算域确定为:主梁中心至速度入口距离为6B,至上、下对称边界的距离为8B,至压力出口的距离为20B,其中B 为桥梁宽度值,主梁模拟区域计布置如图1 所示。
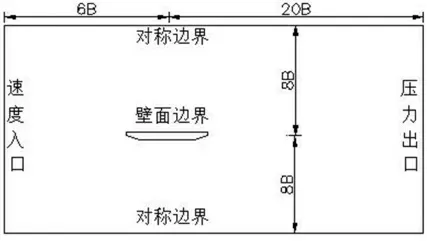
图1 主梁模拟区域布置
网格生成是CFD 软件数值模拟的重要组成部分。为了使计算网格适应流场特征量的变化,需要对流场特征量梯度大的网格进行加密,而特征量梯度小的网格可以适当稀疏,两者之间的网格大小应均匀[2]。网格划分如图2 所示。
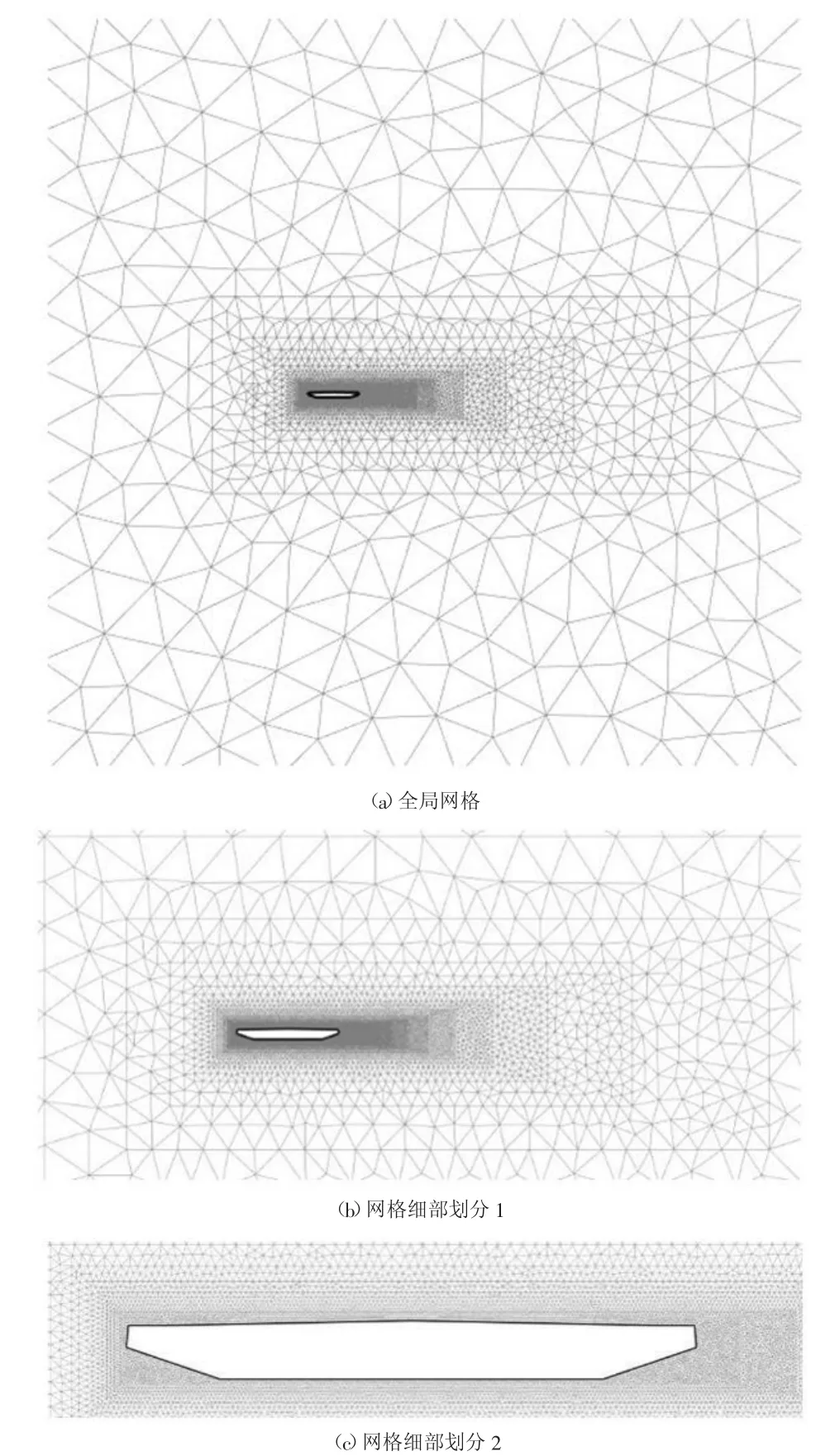
图2 网格划分
2.3 计算工况
考虑风攻角为:±12°、±10°、±8°、±6°、±4°、±2°、0°,共13 个攻角变化工况。
3 风攻角对静力三分力系数影响
3.1 数值模拟结果
指定入口来流速度为20m/s,ρ 取1.225kg/m3,湍流模型采用SST k-ω。通过数值模拟,得到不同攻角下的三分力系数,如图3、表1 所示。

表1 不同攻角下三分力系数
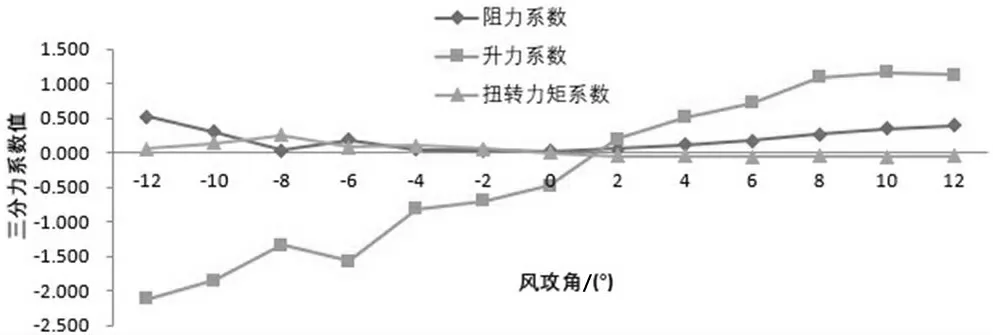
图3 不同风攻角下三分力系数
通过数值模拟可以得出。
阻力系数CD从风攻角-12°向0°基本呈逐渐减小趋势,而从风攻角0°向+12°呈逐渐增大趋势;风攻角0°时为最小值0.024,风攻角-12°时为最大值0.519。
升力系数CL从负攻角到正攻角整体呈逐渐增大趋势,且在负攻角范围内数值为负值,正攻角范围内为正值,风攻角+8°后数值变化较平缓。
扭转力矩系数CM从负攻角到正攻角整体基本呈平缓下降趋势,数值在0 附近波动;在负攻角范围内为正值,而在正攻角范围内为负值。
3.2 规范建议取值
《公路桥梁抗风设计规范》5.3.2 条对部分形式的主梁断面阻力系数给出了式(5)。
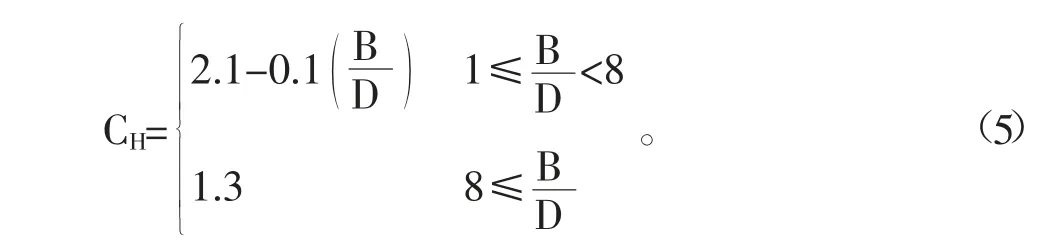
本文桥梁断面阻力系数按照规范建议取值为1.3,与数值模拟值差距较大,主要是因为本文桥梁断面与规范中箱梁断面有区别且规范中未考虑来流风攻角的情况,数值模拟与规范建议结果存在一定的差异,因此对实际较复杂断面,应采用风洞试验或者数值模拟进行分析确定静三分力系数[3]。
4 风攻角对Storohar 数影响
通过对升力系数时程曲线进行FFT 变换,得到涡脱频率f,再代入式(4)求出St,结果如表2、图4 所示。
由表2 及图4 可知,风攻角-10°和-6°时升力系数频谱图卓越频率不明显;风攻角-8°~+6°范围内Storohar 数变化不大,在0.4 附近波动;随着风攻角的增大,Storohar 数也变大[4]。
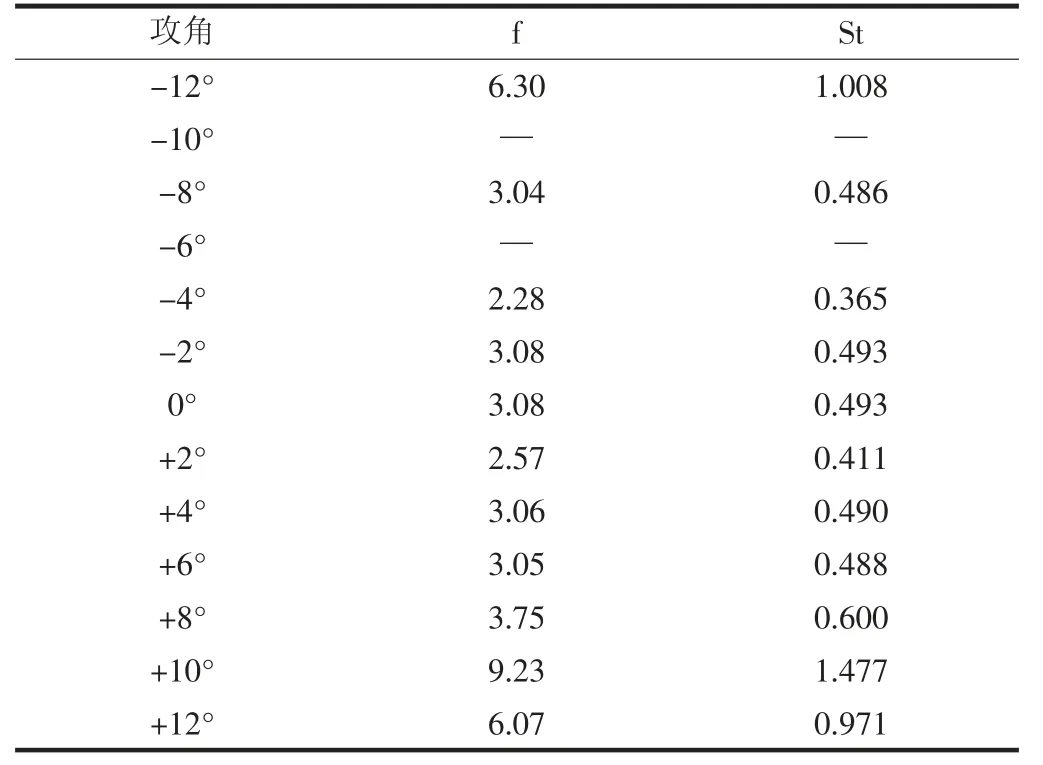
表2 不同攻角下Storohar 数

图4 不同风攻角下Storohar 数
5 结语
本文对某斜拉桥主梁截面周围的静力流动进行了数值模拟,通过分析风在不同攻角下对静三分力系数和Storohar 数的影响,得出以下结论:
(1)阻力系数从风攻角-12°向0°基本呈逐渐减小趋势,而从风攻角0°向+12°呈逐渐增大趋势;风攻角0°时为最小值0.024,风攻角-12°时为最大值0.519。
升力系数从负攻角到正攻角整体呈逐渐增大趋势,且在负攻角范围内数值为负值,正攻角范围内为正值,风攻角+8°后数值变化较平缓。
扭转力矩系数从负攻角到正攻角整体基本呈平缓下降趋势,数值在0 附近波动;在负攻角范围内为正值,而在正攻角范围内为负值。
(2)对实际较复杂断面,应采用风洞试验或者数值模拟进行分析确定静三分力系数。
(3)风攻角-10°和-6°时升力系数频谱图卓越频率不明显;风攻角-8°~+6°范围内Storohar 数变化不大,在0.4 附近波动;随着风攻角的增大,Storohar 数也变大。

