不同风攻角下薄平板断面颤振机理研究
伍波 王骑 廖海黎


摘要: 薄平板在汽轮机末级叶片和风力机叶片等领域获得了广泛的应用,也作为基准对象用于流线型箱梁的颤振研究中。由于不同来流攻角对薄平板气动性能的影响不同,因此研究不同攻角下薄平板的颤振机理,把握其颤振特性,对保障结构安全具有重要意义。以宽高比为40的薄平板模型为研究对象,基于不同风攻角下的颤振导数,采用双模态耦合颤振分析方法,通过对不同攻角下颤振过程中气动阻尼、弯扭运动相位的差异性分析,研究了薄平板在不同风攻角下的颤振机理,指出了影响颤振性能的主要原因。研究结果表明:0°和3°攻角下颤振性能相似,均为扭转主导的弯扭耦合颤振;在5°和7°攻角下,薄平板虽然发生扭转主导的弯扭耦合颤振,但此时非耦合气动力提供的气动正阻尼显著减小,而耦合气动力提供的气动负阻尼增强,因而直接导致了大攻角下薄平板颤振临界风速的显著降低;同时,随着攻角由小到大变化,弯扭运动间的相位差也随之变化,并在7°攻角下发生了翻转式性转变:由扭转运动滞后于竖向运动转变为了竖向运动滞后于扭转运动。研究成果揭示了薄平板在大攻角下颤振性能弱化的气动弹性力学机理,为工程薄平板的颤振设计提供了参考。
关键词: 颤振; 薄平板; 风攻角; 气动阻尼; 运动状态
中图分类号: TU312+.1; U441+.3 文献标志码: A 文章编号: 1004-4523(2020)04-0667-12
DOI:10.16385/j.cnki.issn.1004-4523.2020.04.004
引 言
薄平板断面作为一种基本的气动断面形式,在工程领域具有广泛的应用。飞机机翼、风力机及汽轮机叶片、核反应堆板状燃料组件、桥梁抗风设计、大型风扇叶片等,大都采用平板或类平板断面。随着结构的大型化发展,其长细比增加,如大展弦比叶片在大功率风力机和大功率汽轮机上的广泛应用,因而柔性增大引起的颤振问题也变得越来越突出[1-2]。
作为一种经典的气动弹性失稳现象,薄平板的颤振是在气动负阻尼的作用下发生发散性的弯扭耦合振动。Groninger等[3]发现了燃料板在10 m/s的低速流作用下发生颤振失稳现象。此后,各领域学者相继进行了多项研究,致力于工程中薄平板构件颤振的研究,并对临界风速或流速进行预测[4-6]。近些年来,随着计算机分析技术及理论分析手段的逐渐成熟,针对平板断面气动弹性现象的研究日趋深入。贾明晓等[7]利用CFD数值模拟方法直接模拟了平板断面在颤振临界状态下的尾部旋涡演化规律,研究了导致断面颤振的流场原因。姜伟[8]基于流固耦合的时域分析方法,对某汽轮机末级叶片的颤振问题进行了数值模拟研究。另一方面,桥梁的颤振机理研究也获得了长足发展。杨詠昕在Matsumoto等[9-13]提出的SBSA方法基础上,提出了二维三自由度耦合颤振分析方法,并对薄平板的颤振机理进行了研究[14]。李迺璐等[15]基于Beddoes-Leishman气动模型,研究了旋转水平风机叶片的颤振边界。Chen等[16-18]提出了双模态耦合颤振闭合解法,为颤振机理研究提供了精确理论。
从现有的研究成果来看,基本限于对0°攻角下平板颤振的研究,而攻角不为零甚至更大时的研究则少有涉及。事实上,非零攻角下平板断面的颤振特性研究同样重要。例如,翼型的设计追求较高的升阻比,最大升力系数一般会在一个中等攻角下(比如6°)获得的,而此条件下翼型的颤振性能显得格外重要[19]。风力机和汽轮机的大展弦比叶片也会受到非零攻角来流的影响。此外,山区风和台风的大攻角特性使得风攻角成为了影响山区大跨度桥梁抗风设计的首要因素[20-22],作为流线型箱梁的等代气动断面,平板断面在不同攻角下的颤振特性研究能够为大攻角条件下的桥梁抗风设计提供重要参考。尽管有学者针对不同攻角来流情况下薄平板断面的流固耦合特性、线性及非线性气动力特性以及颤振导数进行研究[23-26],但对于不同攻角下薄平板颤振机理的研究则几乎没有涉及。
考虑到不同攻角下薄平板断面颤振特性研究的不足,本文基于不同风攻角下的薄平板模型的颤振导数,利用双模态耦合颤振分析方法[16-18]研究了不同攻角下气动阻尼、模态频率以及耦合运动相位的变化规律,指出了影响这些参数发生变化的主要因素,继而深入研究了不同攻角下薄平板断面颤振的发生机理,解释了大攻角下薄平板颤振性能弱化的根本原因,为工程薄平板的颤振设计提供了参考。
为清晰地表达上述颤振理论计算流程、運动间相互激励机制以及颤振驱动原理,以扭转模态分支为例,图1给出了运动振幅比、相位差、模态频率修正及模态阻尼计算(即颤振风速搜索)的全流程图。
2 薄平板的颤振计算结果
本试验采用的平板模型长度1.1 m,宽度0.4 m,厚0.01 m,宽高比40,满足工程意义上的薄平板尺寸;同时,为了尽可能的满足理想平板特性,减小平板前缘流动分离,在模型的前后缘均做圆角处理(倒角半径10 mm)。模型断面如图2所示。
计算采用三种不同动力参数,分别对不同攻角下薄平板的颤振性能进行计算,并利用相同动力参数进行自由振动风洞试验,以获得与计算结果对比的颤振试验结果,也由此验证计算结果的正确性。计算参数如表1所示,其中,au表示初始风攻角, wa0/wh0为扭弯频率比。
颤振导数是表征桥梁断面颤振特性的重要参数,在颤振计算中必不可少。2018年,王骑等[26]利用强迫振动试验装置识别了薄平板在不同攻角下的颤振导数,测试结果如图3所示。从结果上看,在0°攻角下,对颤振临界风速起关键作用的几个颤振导数A* 1,A* 2,A* 3,H* 3与理想平板的理论解基本一致[17,26]。其他非关键导数除H* 1外,均与理论值存在一定的差异,在绝对值上大于理想平板的理论值。
颤振导数值会随着风攻角变化而变化,H* 2,H* 4,A* 2,A* 4四个颤振导数变化明显,尤其在7°攻角下,A* 2,A* 4曲线随折算风速的变化趋势出现反向。颤振导数的变化会显著影响断面的颤振特性,包括颤振风速、颤振形态(振幅比、相位差及临界风速)及驱动机理。
颤振计算结果及风洞试验结果对比如表2所示。结果显示,无论是颤振风速还是颤振频率,计算结果与试验结果均具有很好的吻合度,最大计算误差仅为5%。计算结果验证了颤振导数准确性,同时也表明此颤振导数可以作为基础参数,用以揭示不同攻角下薄平板的颤振机理。图4,5给出了薄平板在不同攻角下的,气动阻尼比及模态频率随折算风速的变化曲线。从气动阻尼比的变化规律来看(图4),不同攻角下扭转模态分支对应的气动阻尼比首先达到“由正变负”的状态,即平板在0°到7°的不同攻角下的颤振形态均由扭转模态分支主导。不同攻角下对应气动阻尼比随折算风速的变化曲线表现出了显著差异,表明不同攻角下颤振导数的变化直接导致了气动阻尼比的显著变化;当动力参数相同时,尽管不同攻角下的颤振导数差异较大,但模态频率随折算风速的变化规律却大致相同,且不同攻角下的颤振频率保持一致。
尽管图4和5所示的结果从宏观上解释了气动阻尼比及模态频率随折算风速的变化规律,但是却不能直观地解释影响气动阻尼及模态频率变化的因素并阐释具体的颤振形态,还需要开展进一步的分析。由于Case 1,Case 2及Case 3模态频率及气动阻尼比随折算风速的变化曲线较为相似,限于篇幅,下文仅以Case 2为例,详细探讨薄平板在不同攻角下的颤振机理。
3 不同攻角薄平板的颤振机理〖*2〗3.1 气动阻尼的变化 基于第1节中对气动阻尼比ξ2的推导,气动阻尼比由非耦合项,即扭转运动直接产生的气动阻尼-0.5υA* 2及耦合项,即扭转运动产生的升力导致的气动阻尼和竖向运动产生的扭矩导致的气动阻尼的综合表达式-0.5μυΨ′sinψ′构成。图6给出了不同攻角下,气动阻尼各子项对总阻尼的贡献。从图6中可以看出,在0°,3°和5°攻角的不同折算风速下,非耦合项总是提供气动正阻尼,耦合项总是提供气动负阻尼;在某一折算风速下,系统总阻尼降至零而达到颤振临界点。由于气动负阻尼由耦合运动引起,因此颤振形态表现为弯扭耦合运动。在攻角为7°时,颤振导数A* 2在折算风速为7.5时转变为正值,因此非耦合项在折算风速小于7.5时,非耦合项提供气动正阻尼,在折算风速大于7.5时,则提供气动负阻尼。此时,由于在7°攻角下耦合气动力在全风速范围内均提供气动负阻尼,而A* 2提供的气动正阻尼较小,所以在折算风速小于7.5的某个风速下总阻尼为零,从而发生临界颤振。因此,即使在7°攻角下薄平板在颤振形态上仍表现为耦合气动负阻尼驱动的弯扭耦合颤振,但其颤振形态却与其他攻角下相比有所不同,后续将进行详细阐述。
表3给出了V=7下,气动阻尼子项随攻角的变化情况。由图6可知,在0°攻角和3°攻角下,气动阻尼及其子项分布规律类似,其原因在于在两种攻角下,影响气动阻尼明显的关键颤振导数A* 1,A* 2,H* 3非常接近。同时,由于A* 2取值较大,非耦合项-0.5υA* 2提供的气动正阻尼较大,耦合项-0.5μυΨ′sinψ′提供的气动负阻尼在折算风速大于7后才开始显著增大,因而颤振临界风速较高。在5°攻角下,耦合项气动负阻尼较0°,3°攻角下的值略有增长,非耦合颤振导数A* 2的显著减小导致了气动正阻尼在总阻尼中的比重显著减小,使得总阻尼为零时对应的折算风速更低,颤振性能显著弱化。在7°攻角下,A* 1,A* 4和H* 3产生的显著变化也略增强了耦合气动负阻尼, A* 2的大幅减小导致了非耦合气动正阻尼相比其他攻角有大幅度的减弱(V=7下,耦合正阻尼由0°的2.7%降至0.4%),这是导致该攻角下颤振性能进一步弱化的主要原因。因此,随着攻角的增大,A* 2的显著减小导致的气动正阻尼比重显著降低是薄平板在大攻角下颤振性能弱化的首要原因。
3.2 运动相位差的变化
相位差直观地表现了颤振时竖向和扭转耦合运动形态,决定耦合气动负阻尼的取值。图7分别给出了0°,3°,5°和7°攻角下,耦合力矩与竖向运动间的相位差θ1 、耦合升力与扭转运动的相位差θ3 、耦合升力与竖向运动弄的相位差θ4、扭转运动与竖向运动相位差ψ以及耦合气动阻尼总相位差ψ′随折算风速变化的曲线。图中蓝色数据点为颤振临界风速处的相位差取值。从图7中可以看出,在0°-5°攻角范围内,相位差的变化规律比较类似,θ1 和θ3 随折算风速递减,θ4随折算风速递增;θ1取值较大,为构成ψ′的最主要成分;θ4在小于7的低折算风速区间取值很小,对ψ′及ψ的贡献较小,但在颤振临界风速点及以上区域占据了运动相位差ψ的主要部分,并成为气动阻尼相位差ψ′的第二主要成分,这种现象在小攻角下(0°,3°)更为明显;θ3在高风速区间取值较小,对ψ′及ψ的贡献最小,尤其在小攻角下(0°,3°)更为明显,随着攻角增大,其贡献程度有所提升。 7°攻角下,相位差的变化规律与其他攻角全然不同,θ1 ,θ3和θ4均随折算风速递增;θ1 ,θ3 和θ4对相位差ψ′的贡献均很明显,不同的是,θ1和θ4对于增大相位差作用比θ3的作用显著;更重要的,随着攻角逐渐增大,运动间的相位差ψ逐渐由小攻角下的正值减小至0再逐渐变成负值,说明随着攻角的变化,颤振形态由扭转运动滞后于竖向运动逐渐转变成竖向运动滞后于扭转运动,这是颤振形态在不同攻角下的重大转变。
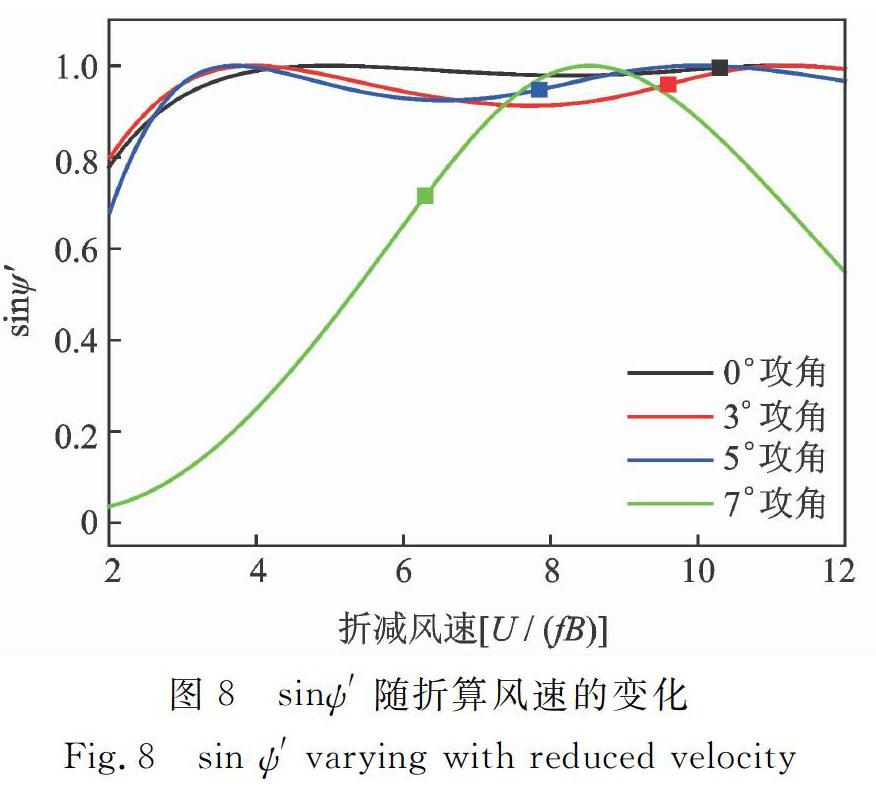
考虑到-0.5μυΨ′sinψ′的构成,耦合气动阻尼总相位差ψ′越接近90°提供的气动负阻尼也越大。图8直接给出了各個攻角及各工况下sinψ′的变化规律。从图8中可以看出,在0°,3°和5°攻角下,sinψ′取值均在0.95以上,可近似取值为1。其原因为,此时气动正阻尼在抑制颤振发生中发挥了较大作用,因此耦合需要达到最大效应以最大程度抵消气动正阻尼,从而引发颤振。考虑到θ1对总相位差贡献最大,此时颤振能量主要由竖向运动产生的耦合力矩项提供。而在7°攻角下,sinψ′取值较小,临界风速处取值下降为0.71,此时运动间的耦合效应减弱。其原因为,此时气动正阻尼很小,耦合产生的气动负阻尼占据绝对主导位置,其不用达到最大值,而只需要大过正阻尼即能引起颤振。
3.3 气动力幅值对颤振的影响
对于同一工况在不同攻角下的颤振性能,除总相位差外(多数情况下接近90°),气动阻尼幅值因子Ψ′是另外一个直接影响耦合气动负阻尼的参数,其值越大气动负阻尼越大。图9给出了在不同攻角下,气动力幅值、动力放大系数Rd2以及气动力幅值因子Ψ′随折算风速变化的迭代结果。从图9(a)可以看出,气动力幅值随折算风速增大而增大,且代表耦合气动升力幅值的项H*22+H*32远大于代表耦合气动力矩项A*12+A*42;同时,对于0°,3°和5°攻角,气动力幅值曲线接近,没有发生明显变化;7°攻角下,气动力幅值明显增大。这是由于H* 2发生了较大变化所致。对于动力放大系数,其值在低风速区均较为接近,随着风速增大,不同攻角下取值差异性也随之增大。
图9(c)中,气动阻尼幅值因子Ψ′曲线在低折算风速区(V<6)都较为接近,而在高折算风速区(V>6),由于Rd2的显著变化,Ψ′也同时发生了较大的离散,说明了在高折算风速下动力系数(或Rd2)变化会显著影响气动阻尼的变化。另一方面,尽管7°攻角下耦合升力幅值H*22+H*32有明显增大,但并未显著增大Ψ′,说明了控制耦合气动阻尼变化的主要因素为Rd2。
本文第3节中提到,尽管各攻角下的颤振形态均为弯扭耦合颤振,且颤振驱动机理也均为耦合气动负阻尼驱动,但7°攻角下的颤振本质却有所不同,本节对此进行具体分析。限于篇幅,本节仅以0°攻角及7°攻角为对象进行对比分析。
通过约束竖向位移(即假想竖向为刚性连接,竖弯频率无穷大),分别对0°攻角及7°攻角进行单自由度颤振计算,气动阻尼变化曲线如图10所示,计算结果如表4所示。
由表4及图10可以看出,对0°攻角进行单自由度颤振计算时,由于A* 2始终为负,系统非耦合气动阻尼始终为正,因此仅在扭转模态下无法激发单自由度扭转颤振,因而0°攻角下薄平板的颤振本质为耦合气动力驱动的弯扭耦合颤振。然而对于7°攻角,即使约束竖向位移,忽略耦合气动效应的影响,系统仍在V=7.3,U=8.94 m/s时发生了单自由度扭转颤振,该风速大于耦合颤振情况下的7.76 m/s。由此表明,7°攻角下,薄平板颤振在扭转颤振对应的折算风速7.3以前发生(A* 2由负转正的交接点)其形态为耦合颤振,此时耦合气动力为系统提供了足够气动负阻尼,而气动正阻尼很小,因此颤振性能受到了很大弱化,导致颤振临界点提前; 此时若约束竖向自由度,防止耦合运动发生,那么颤振风速将为A* 2由负转正的对应的折算风速。
5 结 论
本文采用耦合颤振闭合解理论详细分析了薄平板在0°,3°,5°及7°下的颤振机理和影响颤振性能的主要因素,主要结论如下:
(1)薄平板在0°到7°的不同攻角下均发生以扭转模态分支主导的弯扭耦合颤振。其中,在0°和3°攻角下,耦合气动负阻尼增大是颤振发生的首要因素;在5°攻角下,非耦合气动正阻尼的减小与耦合气动负阻尼的增大共同导致颤振风速显著降低;在7°攻角下,非耦合气动正阻尼的急剧减小是颤振性能显著下降的首要原因。
(2) 在0°,3°及5°攻角下,颤振临界点对应的非耦合阻尼项的相位值sinψ′取值接近于1,表明较强的弯扭耦合效应才足够引发颤振;在7°攻角下,sinψ′取值降低到了0.7,表明較弱的耦合效应即可显著削弱颤振性能,使得颤振临界风速显著降低。
参考文献:
[1] 李 媛. 风力机叶片流固耦合数值模拟[D]. 北京: 华北电力大学, 2013.
Li Yuan. Numerical simulation of fluid structure coupling of wind turbine blade[D]. Beijing: North China Electric Power University, 2013.
[2] 弓三伟,任丽芸,刘火星,等. 汽轮机末级转子叶片流固耦合计算[J]. 热力透平, 2007, 36(3): 153-163.
Gong Sanwei, Ren Liyun, Liu Huoxing, et al. Fluid-solid interaction of rotor blade in last stage of steam turbine[J]. Thermal Turbine, 2007, 36(3): 153-163.
[3] Groninger R, Kane J. Flow induced deflections of parallel flat plates[J]. Nuclear Science and Engineering, 1963, 16(1): 21-26.
[4] Theodorsen T. General theory of aerodynamic instability and the mechanism of flutter[R]. NACA Report No. 496. U.S., National Advisory Committee for Aeronautics, Langley, VA, 1935.
[5] Muthuverrappan G. A note on vibration of a cantilever plate immersed in water[J]. Journal of Sound and Vibration, 1979, 63(3): 385-391.
[6] 张绢花,陆道纲. 窄道流中柔性单板流固耦合数值模拟[J]. 原子能科学技术, 2009, 43(10): 903-909.
Zhang Juanhua, Lu Daogang. Numerical simulation on flow-structure interaction for flexible plate in narrow flow channel[J]. Atomic Energy Science and Technology, 2009, 43(10): 903-909.
[7] 贾明晓,刘祖军,杨詠昕. 平板断面颤振过程中能量输入特性研究[J]. 振动与冲击, 2013, 32(7): 135-140.
Jia Mingxiao, Liu Zujun, Yang Yongxin. Energy input characteristics of a plate section during flutter[J]. Journal of Vibration and Shock, 2013, 32(7): 135-140.
[8] 姜 伟,谢诞梅,陈 畅,等. 基于时域分析法的汽轮机末级叶片颤振预测及分析[J]. 振动与冲击, 2015, 34(11): 194-199.
Jiang Wei, Xie Danmei, Chen Chang, et al. Flutter prediction and analysis for a steam turbine last-stage based on time domain analysis method [J]. Journal of Vibration and Shock, 2015, 34(11): 194-199.
[9] Matsumoto M, Shirato H, Hirai S. Torsional flutter mechanism of 2-D H-shaped cylinders and effects of flow turbulence[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 41-44: 687-698.
[10] Matsumoto M, Okubo K, Ito Y, et al. The complex branch characteristics of coupled flutter[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96, 1843-1855.
[11] Matsumoto M. Aerodynamic damping of prisms [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1996, 59: 159-175.
[12] Matsumoto M, Shirato H, Mizuno K, et al. Flutter characteristics of H-shaped cylinders with various side ratios and comparisons with characteristics of rectangular cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 963-970.
[13] Daito Y, Matsumoto M, Araki K. Torsional flutter mechanism of two edge girders for long span cable stayed bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90: 2127-2141.
[14] 楊詠昕,葛耀君,项海帆. 平板断面扭弯耦合颤振机理研究[J]. 工程力学, 2006, 23(12):1-8.
Yang Yongxin, Ge Yaojun, Xiang Haifan. Research on the coupled bending-torsional flutter mechanism for thin plate sections [J]. Engineering Mechanics, 2006, 23(12): 1-8.
[15] 李迺璐,穆安乐,Balas M J. 基于B-L气动模型的旋转水平风机叶片经典颤振稳定性分析[J]. 振动与冲击, 2015, 34(23): 171-176.
Li Nailu, Mu Anle, Bales M J. Classical flutter stability of rotating horizontal wind turbine blades based on B-L aeroelastic model[J]. Journal of Vibration and Shock, 2015, 34(23): 171-176.
[16] Chen X, Kareem A. Revisiting multimode coupled bridge flutter: Some new insights[J]. Journal of Engineering Mechanics, 2006, 132(10):1115-1123.
[17] Chen X. Improved understanding of bimodal coupled bridge flutter based on closed form solutions[J]. Journal of Structural Engineering, 2007, 133(1): 22-31.
[18] Chen X, Kareem A. Identification of critical structural modes and flutter derivatives for predicting coupled bridge flutter[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 1856-1870.
[19] Tangler J, Somers D. Status of the special purpose airfoil families[R]. Solar Energy Research Inst., Golden, CO, USA; Airfoils, Inc., Hampton, VA, USA, 1987.
[20] 庞加斌,宋锦忠,林志兴. 四渡河峡谷大桥桥位风的湍流特性实测分析[J]. 中国公路学报,2010,23(3):42-47.
Pang Jiabin, Song Jinzhong, Lin Zhixing. Field measurement analysis of wind turbulence characteristics of Sidu river valley bridge site[J]. China Journal of Highway and Transport,2010,23(3): 42-47.
[21] 潘晶晶. 基于实测台风过程的风场特征分析及大跨桥梁风致行为初步研究[D]. 上海:同济大学,2016.
PAN Jingjing. The analysis of characteristic of wind field based on measured typhoon and preliminary study of the wind-induced vibration of large span bridge[D]. Shanghai: Tongji University, 2016.
[22] 李永樂,蔡宪棠,唐 康,等. 深切峡谷桥址区风场空间分布特性的数值模拟研究[J]. 土木工程学报,2011,44(2): 166-122.
Li Yongle, Cai Xiantang, Tang Kang, et al. Study of spatial distribution feature of wind fields over bridge site with a deep cutting gorge using numerical simulation[J]. China Civil Engineering Journal, 2011,44(2): 166-122.
[23] Huang L, Xu Y, Liao H. Nonlinear aerodynamic forces on thin flat plate: Numerical study[J]. Journal of Fluids and Structures, 2014, 44:182-194.
[24] 李永乐,汪 斌,黄 林,等. 平板气动力的CFD模拟及参数研究[J]. 工程力学, 2009, 26(3): 207-211.
Li Yongle, Wang Bin, Huang Lin, et al. CFD simulation and parameter study on aerodynamic force of flat plate[J]. Engineering Mechanics, 2009, 26(3): 207-211.
[25] 吕 坤,张 荻,谢永慧. 不同来流下薄平板流固耦合特性分析[J]. 中国机电工程学报, 2011, 31(26): 76-82.
Lu Kun, Zhang Di, Xie Yonghui. Fluid-structure interaction for thin plate with different flow parameters[J]. Proceedings of the CSEE, 2011, 31(26): 76-82.
[26] 王 骑,李郁林,李志国,等. 不同风攻角下薄平板的颤振导数[J]. 工程力学, 2018, 35(10): 10-16.
Wang Qi, Li Yulin, Li Zhiguo, et al. Flutter derivatives of a thin plate model under different attack angles[J]. Engineering Mechanics, 2018, 35(10): 10-16.
Abstract: Thin flat plates have been widely used in steam turbine last stage blades and wind turbine blades. They are also widely used in bridge flutter analysis. It is well known that flutter performance of section is sensitive to the changing of wind angles of attack. It is of great sense to explore flutter mechanism of thin flat plates under different angles of attack, which helps to understand inner flutter characteristics and ensure structural safety. In this study, flutter derivatives of a thin flat plate with an aspect ratio of 40 under different wind angles of attack are investigated via forced vibration technique. The otherness of aerodynamic damping and phase lag under different wind angles of attack, which helps to understand the flutter mechanism, are analyzed by utilizing bimodal coupled flutter method. It is shown that coupled vertical-torsional flutter dominates the flutter modal under 0° and 3° wind angles of attack. The critical flutter velocity dramatically decreases with increasing wind angles of attack, which is attributed to the increasing negative aerodynamic damping induced by coupled self-excited forces and the decreasing positive aerodynamic damping induced by uncoupled self-excited forces. Moreover, the phase difference between vertical and torsional motion changes significantly with increasing wind angles of attack. The vertical motion lags behind the torsional motion under 7°angle of attack, which is totally contrary to other angles of attack. Major works presented in this study reveal the aerodynamic mechanism of weakening flutter performance of thin flat plates under large wind angle of attack and provide a reference for the flutter analysis of flat plate.
Key words: flutter; thin flat plate; wind angle of attack; aerodynamic damping; motion state

