基于期望补偿的挠性航天器自适应鲁棒主动振动控制

余 臻， 郭 毓， 王 璐, 吴益飞， 郭 健

(南京理工大学 自动化学院， 南京 210094)

随着人类对太空探索与开发的不断深入，航天技术已成为各个国家大力发展的关键技术。现代航天任务愈发复杂，不仅仅局限于对地观测等常规任务，天地往返、太空漫游等已被列入发展规划[1]。组建带有大型挠性附件的航天器已成为目前的发展趋势，其中最著名的大型挠性航天器就是国际空间站，带有太阳能电池帆板、大型空间桁架以及移动维修机械臂等大型挠性附件。我国也于2011年发射了首个目标飞行器和空间实验室“天宫一号”，并于2016年成功发射“天宫二号”。这些大型挠性附件的振动阻尼小，受到太空环境干扰和本体姿轨机动的影响会产生强烈的振动，在真空环境中很难被抑制。强烈的振动不仅会严重影响本体的指向精度和稳定度，进而导致有效载荷失效，还严重威胁着航天器的安全。然而，挠性航天器的系统参数存在不确定性，例如转动惯量，在挠性附件展开前后会产生巨大变化。系统中还有许多其他参数也很难离线准确测量得到。强烈的刚柔耦合、参数不确定和外部环境干扰等因素已成为挠性航天器大角度姿态快速机动控制设计中的难题。因此，具有自适应能力和鲁棒特性以及主动振动控制能力的控制策略在挠性航天器姿态控制系统设计中越来越受到关注。

过去数十年来，航天控制专家将众多控制方法应用于挠性航天器姿态机动控制中。Hu等[2-4]对挠性航天器姿态机动的滑模变结构控制进行了深入的研究，并结合主动振动控制方法对机动过程中挠性附件的振动进行抑制。此外，自适应Back-stepping控制[5]、容错控制[6]及L1自适应控制[7]等均已应用于挠性航天器姿态控制系统设计中。Yao等[8-9]结合自适应控制(Adaptive Control, AC)与确定鲁棒控制(Deterministic Robust Control, DRC)方法的优点，提出了自适应鲁棒控制理论(Adaptive Robust Control, ARC)。通过引入在线参数更新，降低参数不确定的影响，同时通过鲁棒控制律来镇定不确定非线性。由于使用了带有参数投影的自适应律，使得参数估计一直保持在确定的界内，可保证二者结合的有效性[10]。为了降低测量噪声的影响并提高自适应模型补偿的效果，使用期望轨迹信息来计算回归量的思想被纳入ARC设计中，基于期望补偿的自适应鲁棒控制(Desired Compensation Adaptive Robust Control, DCARC)应运而生[11]。对于具有参数和干扰不确定性的挠性航天器系统的姿态控制设计，应用DCARC方法改善姿态控制性能是一个值得研究的课题。

另一方面，大量挠性结构在空间结构中的应用使得针对挠性结构的控制已成为空间控制的一部分。由于对挠性结构的控制精度要求越来越高，被动控制已难以满足高精度控制要求。近年来，采用智能材料传感器与作动器进行主动振动控制的研究不断升温[12]。在众多智能材料中，压电材料由于存在正逆压电效应，可作为传感器与作动器，受到振动控制专家的广泛关注。独立模态控制[13]、应变率反馈(Strain Rate Feedback, SRF)控制[14]、正位置反馈(Positive Position Feedback, PPF)控制[15]等方法已广泛应用于挠性结构的主动振动控制中。其中，PPF控制策略作为一种鲁棒控制方法最早由Goh[16]提出，对控制溢出不敏感。将PPF控制器的频率选取为特定模态的固有频率，可以实现主动阻尼[17]。Hu等将PPF和SRF控制与变结构姿态控制相结合，使挠性航天器在完成大角度姿态快速机动过程中，挠性附件的振动得到抑制。

本文针对一类带有大型挠性附件的航天器大角度姿态快速机动的控制问题，提出了一种将路径规划、基于DCARC的姿态控制以及基于PPF的主动振动控制技术相结合的自适应鲁棒主动振动控制方法。本文结构安排如下：第一节描述了一类粘贴有压电传感器与作动器的挠性航天器动力学模型并提出了控制方案总体设计；第二节设计了基于DCARC的姿态控制器；第三节分别阐述了多模态PPF主动振动控制器与路径规划的设计方法；第四节给出了仿真结果与分析；第五节为本文结论。

1 挠性航天器动力学模型与控制方案设计

1.1 数学模型

对于一类挠性附件表面粘贴有压电传感器和作动器的大型航天器系统，可视为由中心刚体和挠性梁组成。中心刚体相对惯性空间做定轴转动，挠性梁以悬臂方式与其连接。这种模型能够代表一大类的挠性航天器，如卫星-太阳能帆板系统等。使用混合坐标建模方法得到的姿态动力学简化模型为

(1)

式中：J为挠性航天器系统的转动惯量;φ为航天器中心刚体的角位置;Fi为挠性附件第i阶模态和中心刚体的耦合系数(i=1,2,…,n);ηi为挠性附件第i阶模态坐标;d为作用在航天器上的干扰力矩;u为作用在航天器上的控制力矩;Vi为挠性附件第i阶模态阻尼比;ωi为挠性附件第i阶模态固有频率;σi为压电作动器与挠性附件第i阶模态的耦合系数;up为压电作动器的控制电压;n为考虑的模态数目。

式(1)中第一个方程为航天器中心刚体动力学方程，第二个为挠性附件模态方程。其中，系统的转动惯量及外部干扰存在不确定性。中心刚体的运动受到外部干扰以及挠性附件的耦合影响，而挠性附件的振动由中心刚体的姿态运动激发。

控制目标：考虑挠性航天器进行Rest-to-Rest姿态机动，角位置φ从初始姿态角旋转到期望姿态角。通过设计式(1)中的u和up，使得航天器系统在受到外部不确定性干扰影响并带有惯量参数不确定的条件下，能够完成大角度姿态快速机动，并抑制机动过程中挠性附件的振动。

1.2 控制方案总体设计

考虑到挠性航天器存在参数不确定和外部干扰的影响，且需抑制因姿态机动而激发的挠性附件振动，本文提出了一种挠性航天器大角度姿态快速机动自适应鲁棒主动振动控制方案，系统结构如图1所示。首先根据挠性航天器期望的机动角度运用Bang-Coast-Bang(BCB)型路径规划中心刚体角加速度，通过路径参数的选择使得其不易激发挠性附件振动，从而得到期望的姿态角位置路径。采用基于DCARC的姿态控制器跟踪规划的期望路径，使得挠性航天器在存在刚柔耦合、参数不确定以及外部干扰下实现大角度姿态快速机动，并具有满意的动态和稳态性能。在DCARC姿态控制中的自适应模型补偿和带参数投影的自适应律都利用期望路径信息计算回归量，以减少在线计算时间和测量噪声的影响。同时，针对姿态快速机动引起的挠性附件的高频振动，采用多模态PPF控制设计主动振动控制器，通过压电传感器/作动器对挠性附件的振动进行抑制。

图1 挠性航天器自适应鲁棒主动振动控制框图Fig.1 Diagram of adaptive robust active vibration control for flexible spacecraft

2 基于期望补偿的自适应鲁棒姿态控制

2.1 模型变换与假设

将挠性航天器中心刚体动力学方程表示为状态空间方程形式为

(2)

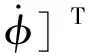
式(2)中第二个方程可改写为

(3)

由于J和Δ存在不确定性，定义需自适应更新的未知参数为θ=[θ1θ2]T=[JΔn]T，则式(3)可表示为

(4)

假设1参数不确定与扰动不确定的范围是已知的，即

θ∈Ωθ={θ:θmin<θ<θmax}

(5)

(6)

式中,θmax=[θ1maxθ2max]T和θmin=[θ1minθ2min]T分别为未知参数θ已知的上、下界，且δ也为已知。式(5)中对向量使用的运算符号“<”在本文中表示对向量中对应元素的大小进行比较。

注1由于采用了主动振动控制，主动增加了挠性附件的阻尼，使得挠性模态的幅值及速率均有界，因此未知总扰动是有界的。此外，未知参数的界一般可测量或估计得到，所以假设1是合理的。

定义被控量为

(7)

式中:e=φ-φd为挠性航天器中心刚体角位置误差;φd为规划的角位置期望路径;k1为正增益。因此，控制目标可转换为控制p。

对式(7)求导并考虑式(3)可得

(8)

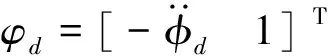
2.2 带参数投影的自适应律

为了确保参数估计始终保持在确定的界内，使用带参数投影的自适应律为

(9)

(10)

2.3 基于DCARC的姿态控制器设计

考虑到式(8)的形式，基于DCARC的姿态控制律设计为

(11)

式中：ua为自适应期望模型补偿。由于使用期望路径信息计算回归量，而非实际状态的在线测量，可以有效减少计算时间，减小测量噪声的影响;us为鲁棒控制律，且由两部分组成

us=us1+us2,us1=-ks1p

(12)

其中，

ks1≥k2+θ1k1

(13)

式中：k2和ks1均为正增益;us2为镇定参数不确定和扰动不确定的鲁棒控制项。将式(11)和式(12)代入式(8)可得

(14)

基于假设1，设计us2满足以下条件

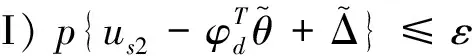
(15)

式中,ε为一个可设计的常数。本文中us2设计为

(16)

其中:h≥||θM||||φd||+δ;θM=θmax-θmin。

2.4 稳定性分析

引理1对于任意的自适应函数τ，带参数投影的自适应律式(9)都具有以下性质[18]

(17)

(18)

定理1对于挠性航天器系统式(1)，采用带有基于参数投影自适应律式(9)的DCARC控制律式(11)和式(12)可保证：

(1) 挠性航天器系统中所有信号均有界，且正定函数是有界的

(19)

(20)

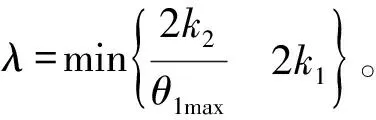
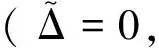
证明：对Vs求导并将式(14)代入可得

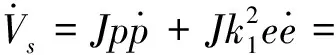
(21)

将式(7)代入，可得

(22)

考虑到式(15)的条件I)以及式(13)

(23)

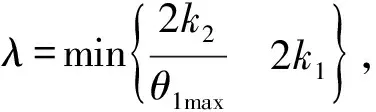
(24)

(25)

对Va求导并将式(22)代入可得

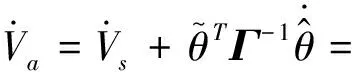
(26)

考虑到式(15)的条件II)以及式(13)和式(18)

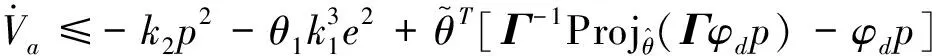
(27)

3 主动振动控制与路径规划

3.1 基于PPF的主动振动控制器设计

本文中考虑航天器的挠性附件表面黏贴有一对压电传感器/作动器，当挠性附件由于振动发生形变，压电传感器会产生电压；当主动振动控制器输出控制电压作用于压电作动器，其会产生力作用于挠性附件，进而主动抑制振动。

由于柔性结构本质上是分布参数系统，具有无穷多个模态，高模态密度会导致“溢出”现象[19]。PPF控制方法由于对溢出不敏感，被广泛应用于柔性结构的主动振动控制中。其工作原理是将柔性结构的位置信息输入给特定的二阶补偿器，再将补偿器的输出乘以一个正增益后反馈给被控结构，因此命名“正位置反馈”。PPF控制可以由以下两个方程描述，其中第一个描述被控柔性结构，第二个表示PPF补偿器[20]

(28)

(29)

式中：z是描述被控柔性结构位移信息的模态坐标;V和ω分别为结构的阻尼比和固有频率;g为正增益;ξ为PPF补偿器输出;Vc和ωc分别为补偿器的阻尼比和频率。其闭环系统的稳定条件为

0

(30)

由于挠性附件的主导模态不止一个，为了抑制多个主导模态的振动，需要使用多模态PPF控制器，即通过将多个PPF控制器并联来实现，其中每个PPF控制器针对一个特定模态，如图2所示。多模态PPF控制由以下方程描述

(31)

(32)

式中：G为增益矩阵;U为参与矩阵；η和ξ分别为被控柔性结构模态和PPF补偿器的坐标向量;Ω和Ωc分别为模态和补偿器的频率矩阵;D和Dc分别为模态和补偿器的阻尼矩阵。其闭环系统的稳定条件为

Ω-UTGU>0

(33)

忽略挠性附件模态方程中中心刚体对挠性附件的耦合影响，可得

(34)

压电传感器的输出电压可表示为附件模态坐标的函数

ys=PTη

(35)

式中，P为系数向量，与传感器的位置、尺寸、材料等因素相关。因此，多模态PPF补偿器为

(36)

式中，X∈Rb×c为设计矩阵，其所有元素均为1，且b为所需控制的模态数目，c为所使用的传感器/作动器对的数目。根据多模态PPF控制的原理，压电作动器的控制电压设计为

up=XTGξ

(37)

关于PPF补偿器频率ωc的选取，有三种情况：主动挠性、主动阻尼和主动刚度。为了产生最大阻尼作用，期望实现主动阻尼情况，即补偿器频率ωc应选择与被控结构的固有频率ω接近。而阻尼比Vc的选择，常需要权衡闭环系统的鲁棒性和主动阻尼性能进行折衷考虑。

图2 多模态PPF控制框图Fig.2 Diagram of multi-modal PPF control

3.2 BCB型机动路径规划

为了在指定时间内尽快完成挠性航天器姿态大角度Rest-to-Rest机动，快速性是需要考虑的问题之一。然而，由于航天器系统存在强烈的刚柔耦合，若中心刚体机动过快，会激发挠性附件的强烈振动。因此，需要在执行机构能力受限和角速度测量受限的情况下，规划平滑的期望机动路径。显然，中心刚体的角位置期望参考轨迹若为阶跃信号，则初始阶段较大的误差会导致执行机构的强烈动作，极易激发附件振动。目前，大角度快速机动路径一般划分为加速、匀速和减速三个阶段，以此平滑姿态运动的过渡过程。

在众多路径形式中，BCB型路径[21]形式简单，直接将加速段与减速段的角加速度设计为大小相同方向相反的常值，匀速段角加速度为零。根据机动时初始角度和期望目标角度，并综合航天器最大角加速度和最大角速度的限制可知，BCB型路径的确定只需要两个参数，即机动过程中航天器中心刚体期望角加速度以及加速段与减速段时间之和。对于路径参数的选择，本文作者在文献[22]中从频谱分析的角度出发，提出了一种兼顾机动快速性和稳定性的BCB型机动路径参数的选择方法。其主要思想是使用DFT(Discrete Fourier Transform)推导得到规划的期望路径的频谱表达式，使得其主频避开挠性附件的主导模态频率，且期望路径的频谱在附件各阶模态频率处的幅值尽量低；同时综合考虑路径参数与机动时间的关系，折衷选择。这里仍用此方法选择BCB型机动路径参数，使得挠性航天器中心刚体角位置的期望路径不易激起挠性附件的振动。

4 仿真分析

4.1 仿真参数

通过数值仿真验证本文所提控制方法的有效性，采用文献[23]中所给出的挠性航天器的物理参数。航天器转动惯量标称值为J=24.62 kgm2，挠性附件前五阶模态的频率分别为ω1=2.580 9 rad/s，ω2=19.329 6 rad/s，ω3=57.938 3 rad/s，ω4=117.971 5 rad/s，ω5=199.687 1 rad/s，阻尼比为V1=V2=V3=V4=V5=0.002，耦合系数分别为F1=3.361 7 kg1/2m，F2=0.419 8 kg1/2m，F3=0.138 4 kg1/2m，F4=0.067 7 kg1/2m，F5=0.039 9 kg1/2m。包含常值与周期性干扰的干扰力矩为d=1.4×10-4sin(0.001t+0.89)+4.3×10-5Nm，最大角加速度和角速度限制为alimit=0.4 °/s2，Vlimit=2.5 °/s。假设航天器需完成-30°～30°大角度姿态机动，且初始和最终期望角速度均为0 °/s。在仿真中，未知参数的上下界分别设为θmax=[30 0.1]T和θmin=[20 -0.1]T。使用BCB型路径规划姿态过渡，且路径参数取为a=0.2 °/s2，T=25 s。

4.2 仿真结果

根据航天器任务要求，考虑了以下四个性能指标来比较分析不同控制方案的优劣：

(1)机动时间ts,姿态角位置和角速度误差均进入5×10-4°和5×10-4°/s误差带所需的时间，评价挠性航天器机动的快速性。

(2)最大误差em,机动过程中姿态角位置误差绝对值的最大值，评价挠性航天器的动态平稳性。

(3)指向精度pm,计算从100～200 s的姿态角位置误差均方根值，评价挠性航天器的稳态性能。

(4)稳定度ps,计算从100～200 s的姿态角速度误差均方根值，评价挠性航天器的稳定性能。

在仿真中采用两种控制方案实现上述任务：

(2)DCARC+PPF,将DCARC姿态控制与PPF主动振动控制相结合，其中DCARC控制律参数与(1)中相同。本文仅针对附件前两阶主导模态设计多模态PPF控制器，且控制参数设为g1=0.135，Vc1=0.5，ωc1=2.6 rad/s，g2=0.188，Vc2=0.5，ωc2=19.4 rad/s。

两种方案的仿真结果如图3～图6所示。图3和图4分别为挠性航天器中心刚体的姿态角位置和角速度误差曲线，从图中观察到，DCARC姿态控制器在60 s之前就使角位置和角速度误差均进入5×10-4°和5×10-4°/s误差带；而采用DCARC+PPF时，航天器机动时间缩短至45 s左右，且角位置和角速度误差进一步减小。航天器挠性附件前两阶模态的响应曲线分别如图5和图6所示，采用DCARC时前两阶模态的高频振动被激发，特别是第二阶模态；而采用DCARC+PPF时，前两阶模态的高频振动被有效抑制。综上，本文所提的自适应鲁棒主动振动控制方法可在实现挠性航天器大角度姿态快速机动高精度控制的同时，有效抑制挠性附件的振动。

(a) (b) (a) (b)图3 姿态角位置误差曲线 图4 姿态角速度误差曲线Fig.3 Angular position error Fig.4 Angular velocity error

(a) (b) (a) (b)图5 第一阶模态响应曲线 图6 第二阶模态响应曲线Fig.5 Response of the first mode Fig.6 Response of the second mode

使用两种不同控制方案时挠性航天器系统的性能指标如表1所示。

表1 使用两种不同控制方案时系统性能指标

由表1中数据可以看出：

对于机动时间ts，采用DCARC+PPF控制方法，挠性航天器系统可在44.83 s内完成姿态机动控制。而使用DCARC方法，则需要57.92 s。因此，DCARC+PPF方法在挠性航天器姿态机动的快速性方面更优越。

对于最大误差em，采用DCARC+PPF控制方法时挠性航天器姿态机动过程中的最大误差为6.40×10-3°，优于DCARC方法。因此，DCARC+PPF方法在挠性航天器姿态机动的平稳性方面表现更好。

对于指向精度pm，采用DCARC+PPF控制方法时挠性航天器姿态机动控制的指向精度达到2.55×10-8°，优于DCARC方法。因此，在挠性航天器姿态机动的稳态性能方面，DCARC+PPF方法效果更佳。

对于稳定度ps，采用DCARC+PPF控制方法时，挠性航天器姿态机动控制的稳定度可达4.42×10-11°/s，相比于DCARC方法，稳定度提高了四个数量级。因此，DCARC+PPF方法在挠性航天器姿态机动的稳定性能方面表现更优。

综上，对于挠性航天器姿态机动控制的四个关键性能指标，本文所提DCARC+PPF方法均表现优越。因此，可实现挠性航天器大角度姿态快速机动，并有效抑制挠性附件的振动。

5 结 论

针对一类挠性附件粘贴有智能材料传感器与作动器的航天器进行大角度姿态快速机动的高精度控制问题，提出了一种结合路径规划、基于DCARC的姿态控制与基于多模态PPF的主动振动控制技术的自适应鲁棒主动振动控制方法。使用BCB型路径规划挠性航天器大角度姿态机动过程中的角位置，通过合适的参数选择得到不易激起挠性附件振动的期望机动路径。采用DCARC姿态控制器对规划的期望路径进行跟踪，使挠性航天器在存在外部干扰和参数不确定下完成大角度姿态快速机动的同时，具有满意的动态和稳态性能。由于在DCARC中使用期望路径信息计算回归量，可减少测量噪声的影响，缩短在线计算时间。同时，为了进一步抑制挠性附件的高频振动，设计了以压电智能材料作为传感器和作动器的多模态PPF主动振动控制器，有效提高了挠性附件的阻尼，使得航天器系统的稳定度大幅提高。仿真结果表明所提控制方法在挠性航天器大角度姿态机动的快速性、平稳性和稳态性能方面均表现优越，且对机动过程中挠性附件的振动抑制效果明显。

[ 1 ] 包为民. 航天飞行器控制技术研究现状与发展趋势[J]. 自动化学报, 2013, 39(6): 697-702.

BAO Weimin. Present situation and development tendency of aerospace control techniques [J]. Acta Automatica Sinica, 2013, 39(6): 697-702.

[ 2 ] HU Q L, MA G F. Variable structure control and active vibration suppression of flexible spacecraft during attitude maneuver [J]. Aerospace Science and Technology, 2005, 9(4): 307-317.

[ 3 ] HU Q L. Variable structure maneuvering control with time-varying sliding surface and active vibration damping of flexible spacecraft with input saturation [J]. Acta Astronautica, 2009, 64(11): 1085-1108.

[ 4 ] 胡庆雷, 马广富. 带有输入非线性的挠性航天器姿态机动变结构控制[J]. 宇航学报, 2006, 27(4): 630-634.

HU Qinglei, MA Guangfu. Variable structure control for flexible spacecraft with input nonlinearities during attitude maneuver [J]. Journal of Astronautics, 2006, 27(4): 630-634.

[ 5 ] HU Q L, LI B, HUO X, et al. Spacecraft attitude tracking control under actuator magnitude deviation and misalignment[J]. Aerospace Science and Technology, 2013, 28(1): 266-280.

[ 6 ] JIANG Y, HU Q L, MA G F. Adaptive backstepping fault-tolerant control for flexible spacecraft with unknown bounded disturbances and actuator failures [J]. ISA Transactions, 2010, 49(1): 57-69.

[ 7 ] LEE K W, SINGH S N. L1 adaptive control of flexible spacecraft despite disturbances [J]. Acta Astronautica, 2012, 80: 24-35.

[ 8 ] YAO B, TOMIZUKA M. Adaptive robust control of SISO nonlinear systems in a semi-strict feedback form [J]. Automatica, 1997, 33(5): 893-900.

[ 9 ] YAO B,TOMIZUKA M. Adaptive robust control of MIMO nonlinear systems in semi-strict feedback forms [J]. Automatica, 2001, 37(9): 1305-1321.

[10] YAO B. High performance adaptive robust control of nonlinear systems: a general framework and new schemes [C]// Proceedings of the 36th Conference on Decision and Control. San Diego: IEEE, 1997. 3: 2489-2494.

[11] YAO B. Desired compensation adaptive robust control[J]. Journal of Dynamic Systems, Measurement, and Control, 2009, 131(6): 1-7.

[12] CHOPRA I. Review of state of art of smart structures and integrated systems[J]. AIAA Journal, 2002, 40(11): 2145-2187.

[13] MEIROVITCH L, OZ H. Modal-space control of distributed gyroscopic systems [J]. Journal of Guidance, Control, and Dynamics, 1980, 3(2): 140-150.

[14] SONG G B, KOTEJOSHYER B. Vibration reduction of flexible structures during slew operations [J]. International Journal of Acoustics and Vibration, 2002, 7(2): 105-109.

[15] YU Z, GUO Y, WU L P, et al. Adaptive positive position feedback for multi-modal vibration control of a flexible beam[J]. International Journal of Modelling, Identification and Control, 2015, 24(3): 224-234.

[16] GOH C J. Analysis and control of quasi distributed parameter systems [D]. Pasadena: California Institute of Technology, 1983.

[17] SONG G B, SCHMIDT S P, AGRAWAL B N. Active vibration suppression of a flexible structure using smart material and a modular control patch [J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2000, 214(4):217-229.

[18] YAO B, TOMIZUKA M. Smooth robust adaptive sliding mode control of manipulators with guaranteed transient performance [J]. Journal of Dynamic Systems, Measurement, and Control, 1996, 118(4): 764-775.

[19] BALAS M J. Active control of flexible systems [J]. Journal of Optimization Theory and Applications, 1978, 25(3): 415-436.

[20] FANSON J L, CAUGHEY T K. Positive position feedback control for large space structures [J]. AIAA Journal, 1990, 28(4):717-724.

[21] CREAMER G, DELAHUNT P, GATES S, et al. Attitude determination and control of Clementine during Lunar mapping [J]. Journal of Guidance, Control, and Dynamics,1996, 19(3): 505-511.

[22] YU Z, ZHONG C X, GUO Y. Spectral analysis and parameter selection for BCB attitude maneuver path of flexible spacecraft [C]// Proceedings of IEEE International Conference on Information and Automation. Yinchuan: IEEE, 2013: 729-734.

[23] 胡庆雷. 挠性航天器姿态机动的主动振动控制[D]. 哈尔滨: 哈尔滨工业大学, 2006.