近、远场强震下深水桥梁群桩基础的非线性响应及损伤特性
江 辉, 王 志, 白晓宇, 曾 聪, 王 敏
(1.北京交通大学 土木建筑工程学院,北京 100044; 2.中国土木工程集团有限公司,北京 100038)
群桩基础以其造价低廉、施工方便等优点,在跨海、跨江及跨库区深水桥梁工程中得到广泛应用,如我国苏通长江大桥、杭州湾大桥和港珠澳大桥等深水桥梁,均采用了大量的桩基础。然而,桩基础往往也是地震中的易损部位和薄弱环节,如1964年日本新潟地震、1976年我国唐山地震、1989年美国Loma Prieta地震及1995年日本阪神地震中,均出现了严重的桥梁桩基震害,主要震害形式包括桩土脱离、桩基与承台连接处开裂、一定深度处桩基发生严重剪切、弯曲破坏等。
相对于陆上桥梁,由于地震下墩(桩)、水之间的动力相互作用效应,深水桥梁的振动特性和动力响应均可能发生明显改变[1-2]。因此,充分认识地震激励下动水压力对深水桥梁动力响应的影响,尤其是强震下深水桥梁群桩基础的非线性动力行为与损伤特性,对于新建深水桥梁抗震设计及已建桥梁抗震评估均具有重要意义。
对于陆上群桩基础桥梁,Kimura等[3]采用弹塑性动力分析方法研究了桩身的损伤分布特性。叶爱君等[4]采用Pushover静力方法,对桥梁群桩基础抗震性能的影响因素及改善措施进行了分析。江辉等[5]采用基于性能点轨迹法的非线性静力分析方法,发展了一种可综合考虑桩-土相互作用的地基土柔度效应、运动学效应及阻尼效应的桩基础RC桥梁抗震性能评估方法。
对于群桩基础水中桥梁的抗震研究,随着新世纪以来我国深水桥梁的大规模建设,我国学者开展了创新性工作。魏凯等[6-7]分别采用模型试验和数值模拟两种方法,对比了不同水深下桥梁群桩基础的流固耦合动力特性,并发展了适用于高桩承台基础动水效应计算的数值-解析混合算法。黄信等[8]分别采用Morison方程法和辐射波浪理论,研究了考虑土-结构相互作用时双向地震作用下动水效应对桩基桥墩地震响应的影响。宋波等[9]提出了圆形高桩承台动水压力的简化计算方法。Wei等[10]以桥梁群桩基础-水耦合系统为对象,采用模型试验方法验证了基于势流体理论的完全数值计算法(流固耦合有限元法)的有效性。
对既有研究的总结表明,当前针对深水桥梁群桩基础的研究主要集中于弹性结构,而在强烈地震下,结构有可能进入非线性损伤状态。黄麟等[11]对2008年汶川地震后庙子坪岷江大桥桥墩水下部分的检测发现,该桥5#主墩墩底裂缝宽度最大达到0.8 mm,且环向基本连通,进入严重的非线性状态。黄信等[12]研究发现,动水压力作用下考虑桥墩混凝土材料非线性时的地震响应大于弹性桥墩结构,应引起注意。
本文以某跨江深水桥梁为对象,建立考虑桩基础及墩底塑性变形集中部位非线性力学行为的等效群桩基础模型,并计入动水效应和桩-土相互作用的影响,选取六组共12条代表性的近、远场地震记录为激励,对深水桥梁群桩基础在近、远场地震作用下的非线性动力响应和损伤分布特征进行了较为系统的对比分析。
1 深水桥梁群桩基础非线性分析模型
1.1 算例概况
选取跨越松花江的某大型梁式桥为研究对象,该桥全长3 000 m,由南引桥、南航道桥、中航道桥、北航道桥、北引桥组成,按Ⅷ度(0.2g)抗震设防,桥址所在场地类型为Ⅲ类。选取该桥中航道桥主墩为研究对象,墩高17 m,3 m×4.8 m矩形截面,墩顶上部结构质量为3 000 t。该墩之下是由排列方式为3×3的9根混凝土钻孔灌注桩组成的方形群桩基础,桩总长58 m,桩径1.8 m,桩中心距4.5 m,河床面以上部分的自由段桩长为9.54 m,正方形承台厚3 m,边长12 m。
桩基、承台以及墩柱均采用C40混凝土和Ⅱ级钢筋,单桩纵向主筋采用36Φ28的HRB335钢筋,全截面配筋率为0.86%;箍筋采用R235钢筋,体积配箍率为0.38%;保护层混凝土厚度为6 cm。群桩基础立面图、平面图如图1(a)所示,图中单位为cm,桥墩、承台和桩基采用C40混凝土;墩、桩截面配筋图如图1(b)所示,图中单位为mm,保护层厚度为60 mm。
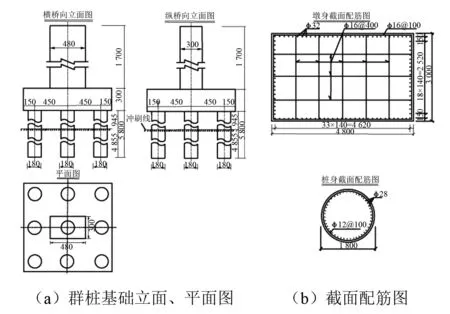
图1 群桩基础结构示意图Fig.1 Prototype of the group-piles foundation
1.2 群桩基础非线性分析模型的建立
为了研究强震下结构损伤在群桩基础各部位的分布特性,采用SAP2000有限元软件建立群桩基础的非线性有限元计算模型。其中,墩底潜在塑性区域以外的桥墩部分采用Beam弹性梁单元模拟,承台采用Solid实体单元模拟,墩顶上部结构质量采用Mass集中质量单元模拟,墩底潜在塑性区及群桩桩体全部采用Link塑性连接单元模拟[13]。
1.2.1 墩、桩非线性力学行为模拟
群桩基础的损伤状态主要由墩底潜在塑性区及桩身的塑性变形能力确定。根据桥墩和单桩的截面尺寸及配筋,采用XTRACT软件进行不同高度处截面的弯矩-曲率(M-φ)分析,可得到各截面的屈服曲率φy、极限曲率φu,以及屈服弯矩My和极限弯矩Mu,以确定非线性滞回模型的骨架曲线。恢复力模型采用Takeda三线性滞回模型模拟,如图2所示。由于地震作用过程中桥墩和群桩的轴力不断变化,既有研究表明[14],地震下的动轴力对截面滞回模型参数取值的影响不可忽略,本文采用文献[15]所提出的等代定轴力考虑动轴力对滞回模型参数的影响。所得滞回模型参数如表1所示,给出了墩底及不同高度处桩身截面的滞回参数。为了适当降低数值模拟的工作量,在保证计算精度的前提下将桩身沿高度分为七种代表性截面,冲刷线以上划为一段,冲刷线以下的分段及所对应的滞回参数见表1。
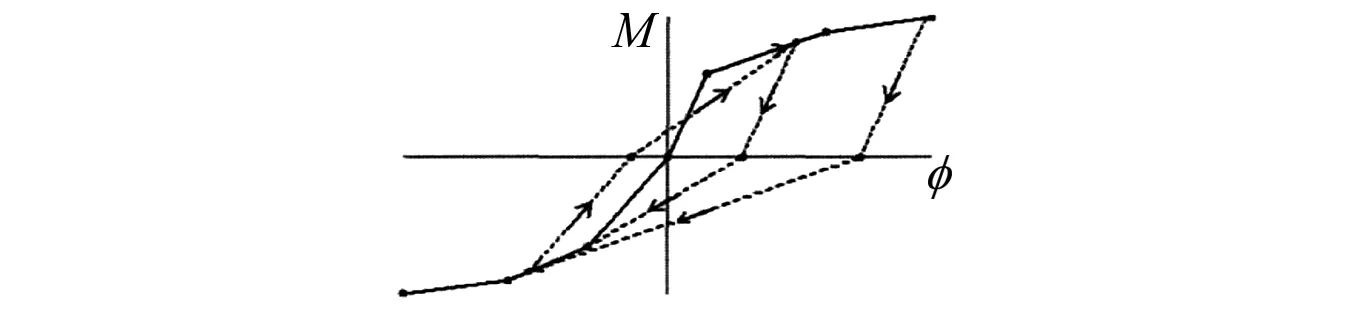
图2 Takeda三线性滞回模型Fig.2 Takeda trilinear hysteretic model

表1 滞回模型参数表
1.2.2 桩-土相互作用模拟
为了考虑桩和桩周土之间的动力相互作用,沿桥轴横向和纵向分别设置土弹簧进行模拟。依据地勘资料,当土层厚度大于等于3 m时,每3 m分为一层,当土层厚度不足3 m时,单独作为一层。桩-土相互作用弹簧的初始弹性刚度依据“m法”计算,各土层弹簧的弹性水平刚度取值如表2所示。

表2 土弹簧初始水平刚度取值
客观而言,“m法”将桩侧土视为弹性体,只适用于一般水平地震下桩顶位移较小时,而在强震下,桩侧土体很有可能进入非线性状态,导致较大的桩顶位移,此时“m法”不再适用。p-y曲线法可以较好地考虑桩-土相互作用中土的非线性特性。燕斌等[16]将p-y曲线法和“m法”计算结果对比后发现,将m值适当修正后可以得到合理的桩基础动力响应。因此,本文分别采用p-y曲线法和“m法”建立桩-土作用模型进行计算,根据两种方法下桩顶位移相一致为原则对m值进行修正。限于篇幅,文中未列出不同PGA (Peak Ground Accelerations)所对应的刚度修正值。为了验证上述处理方法的准确性,以表5中所示6条近场地震波(PGA=0.2g)为输入开展动力时程分析,图3给出了p-y曲线法模型和“m法”模型的桩身响应均值对比。可看出,对于桩身弯矩、剪力、位移,未修正的“m法”计算结果和p-y曲线法差别较为明显,而修正后的“m法”结果则和p-y曲线法吻合很好。因此,本文中采用修正m值开展动力计算。
1.2.3 动水效应的计算方法
对于结构与水体之间的动水效应,采用附加质量法计算。对于桩(墩)周动水引起的等效附加质量,采用Jiang等[17]所提出的简化公式计算;对于承台侧面动水引起的等效附加质量,采用文献[6]等所提出简化公式计算。
①桩(墩)周动水效应计算方法

图3 近场地震波作用下(PGA=0.2g)两种方法桩身响应均值对比Fig.3 Comparison of average responses using two methods under near-fault earthquakes(PGA=0.2g)
Jiang等研究发现,当忽略自由表面波和流体压缩性的影响时,由墩柱刚体运动和弹性振动所引起的动水附加质量M(1)、M(2)基本相等,可进行等效计算。以此为基础,构建覆盖面较宽的深水墩柱模型库(直径D为2~30 m,墩柱高H为2D~200 m),采用辐射波浪理论计算墩柱的动水附加质量并经参数拟合,得到圆形截面墩柱动水效应的简化算法,见式(1)。以近、远场地震波和简谐荷载为激励,采用基于势流体理论的完全数值法验证了该简化算法在深水墩柱动力响应计算中的有效性,并和Morison方程法[18]、Goto和Toki等公式[19]对比,证明所建议简化算法具有计算精度高、适用范围广的优点
(1)
式中:M(1)为单位高度水体质量(等效于墩(桩)刚体运动引起的附加质量);Mwater为单位高度墩(桩)所排开水的质量;Cαi为刚体运动附加质量系数;ρ为水体密度;a为墩(桩)半径;HW为墩(桩)入水深度;Zi为第i单元所对应的水深。
对于本文算例矩形截面桥墩动水效应的计算,需将其等效成圆形截面(见图4)[20],并引入动水附加质量修正系数KC
(2)

(3)
为了讨论不同水深的影响,设定以下4种水深(HW)工况:工况Ⅰ——HW=0 m(无水);工况Ⅱ——HW=9.54 m(水面位于承台底);工况Ⅲ——HW=12.54 m(水面位于承台顶);工况Ⅳ——HW=22.54 m(水面位于承台顶面以上10 m处)。依据以上计算方法,可计算得到不同水深下群桩基础的动水附加质量如表3所示。不同工况下,冲刷线以上桩身分为10段,每段长0.954 m,对应表中序号1~10;承台沿高度分为3段,每段厚1 m,对应表中序号11~13;水中墩身分为10段,每段长1 m,对应表中序号14~23。

图4 不同截面的换算关系Fig.4 Sketch of equivalent section

表3 群桩模型附加质量表
②承台动水效应计算方法
对于承台这种大体积混凝土,其动水附加质量的计算方法和墩、桩类的细长柱体存在差别,不仅与承台迎水面面积、水深有关,还与承台振动周期相关[21]。文献[6]采用3D势流体单元和实体单元建立承台-水耦合模型,基于势流体模型和附加质量模型周期相等的原则给出了承台动水附加质量ma的计算方法
(4)
式中:Tnw、Tw分别为承台在无水及一定水深下的自振周期;mc为承台质量。
根据上述原则,建立桥梁单墩-群桩基础的有限元模型,不同高度处墩、桩及承台的动水附加质量分别采用式(3)和式(4)计算确定,并采用节点质量单元在模型中予以施加。所建立的完整模型如图5所示,当水面刚好到达承台底面时,其前6阶自振周期如表4所示,其前4阶模态的振型如图6所示,与典型桩基础的振动特性相匹配。

表4 群桩基础模型前6阶自振周期
2 近、远场强震记录选取
在进行近、远场强震作用下群桩基础的非线性动力响应和损伤特性对比分析时,为了确保所选地震记录的科学性和代表性,按照以下原则选取:①为了尽可能在同等震源特性条件下实现近、远场效应的对比,分别选取同一典型地震下的近、远场记录;②所有地震事件的震级(M)>6.0级,按照深水桥梁所处的场地条件,记录所在场地类别为Ⅲ类;③对于近场记录,其所在台站的断层投影距离不大于10 km,且应具有明显的长周期脉冲波形,脉冲持时Tp>1 s;④近场地震波的PGV/PGA(峰值速度与加速度之比)>0.1。

图5 等效群桩基础有限元模型Fig.5 Equivalent model of the group-piles foundation
根据上述原则,分别从1979年Imperial Valley、1989年Loma Prieta、1992年Cape Mendocino、1994年Northridge、1995年Kobe和1999年Kocaeli Turkey地震中分别选取了6条具有明显脉冲效应的近场记录和6条远场记录。限于篇幅,这里未列出各条记录的加速度时程图,记录的基本参数如表5所示。12条记录的加速度谱及近、远场均值谱如图7所示,可看出,近场反应谱峰值段较宽,下降较平缓,远场反应谱峰值段较窄,在较小的周期T时达到峰值,之后迅速下降并趋于平缓。

图6 群桩基础模型前4阶自振形态Fig.6 First four vibration modes of the group-piles foundation
3 近、远场地震下群桩基础动力响应对比分析
为了对比不同水深下群桩基础在近、远场地震下动力响应的差异特性,考虑到模型在纵、横桥向的对称性,以所选用的12条地震记录为输入,沿顺桥向激励开展非线性时程计算。图8为群桩平面布置及单桩编号,可看出,因9根桩呈方形对称分布,可将其分为四组:1#、3#、7#、9#桩是角桩,为第一组;2#、8#桩是横桥向边中桩,为第二组;4#、6#桩是顺桥向边中桩,为第三组;5#桩是中心桩,可单独列为第四组。基于代表性,后续可先选取1#、2#、4#、5#桩进行对比分析。

表5 所选取的近、远场地震波


图7 地震波加速度谱(阻尼比为5%)Fig.7 Acceleration spectra of the selected earthquake records (damping ratio=5%)

图8 单桩编号示意图Fig.8 Diagrammatic sketch of the piles in the group-piles foundation
限于篇幅,以水深HW=9.54 m时为例,图9给出了群桩基础在PGA=0.2g时动力响应峰值的均值(包络值)沿不同高度h分布的对比。从图9中可看出,对于弯矩响应,从桩底到冲刷线,弯矩先增大后减小,在冲刷线以下一定位置(第5与第6土层交界处附近)达到土层内部的最大值,之后从冲刷线往上又显著增大,并在桩顶处达到整个桩身的最大值。对于剪力,其分布特征和弯矩类似,只是土层内部峰值出现的位置有所差异。对于位移响应,从桩底向上不断增大。
从图9中还可看出,近、远场地震下,1#、2#、4#、5#4根桩的动力响应分布特征及量值都相一致,因此后文以1#角桩为代表进行分析。此外,近、远场地震下的响应对比表明,近场地震下,轴力P、弯矩M、剪力Q和位移d的峰值分别为8.14 MN、4.21 MN·m、0.38 MN和21.24 cm,而在远场地震下分别对应为6.40 MN、2.03 MN·m、0.15 MN和5.16 cm,近场地震下群桩基础的动力响应明显大于远场。
为了量化对比近、远场地震下群桩基础动力响应的差异,定义无量纲指标—动力响应差异率E(M,Q,d,P),如式(5)所示。图10给出了水深HW=9.54 m时在PGA=0.2g时1#桩E指标沿高度方向(桩底到桩顶)的分布。可看出,不同高度处,E均为正值,表明近场地震下群桩基础的动力响应均大于远场,其中,弯矩、剪力、位移的最大增幅分别出现在冲刷线以下不同深度处,轴力的最大增幅则出现在桩顶处。剪力、弯矩、位移和轴力的最大增幅分别为141.2%、213.9%、333.4%和64.2%。通过上述分析可知,相比远场地震,具有明显脉冲波形的近场地震会引起群桩结构更大的动力响应。
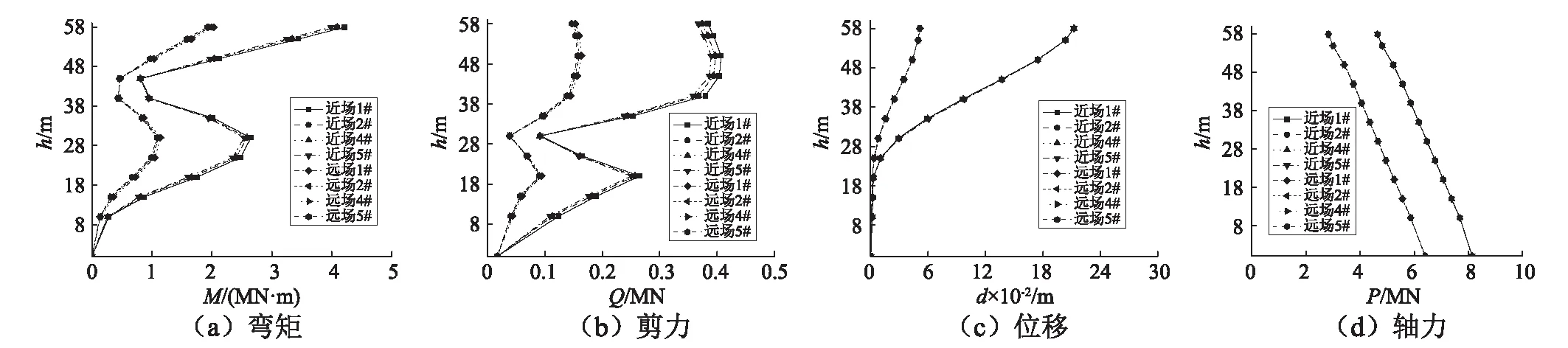
图9 近、远场地震下各桩动力响应包络图Fig.9 Envelope of the dynamic response of the piles under near-fault and far-field earthquakes
(5)
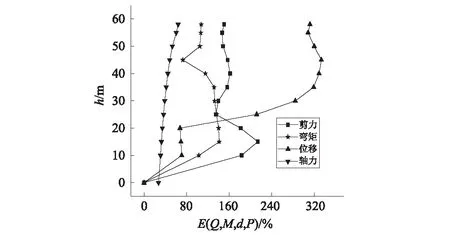
图10 近、远场地震下1#桩动力响应差异率分布Fig.10 Distribution of the dynamic response difference ratio of 1# pile under near-fault and far-field earthquakes
为了分析不同水深下桩身近、远场地震动力响应的差异率,以1#桩为对象,图11给出了近、远场地震下1#桩动力响应差异率随墩高的分布(PGA=0.2g)。从图11中可看出,桩身动力响应总体增幅随水深的增加先增大后减小。桩身弯矩、剪力、位移最大增幅位于冲刷线下不同深度处,轴力的最大增幅位于桩顶。桩身轴力、弯矩、位移和剪力的最大增幅分别为64.2%,150.6%,333.4%及227.2%。
4 群桩基础损伤特性对比分析

图11 不同水深下近、远场地震下1#桩动力响应差异率(PGA=0.2g)Fig.11 Distribution of the dynamic response difference ratio of 1# pile under near-fault and far-field earthquakes under different water depths(PGA=0.2g)
为了对比近、远场地震下群桩基础结构损伤的分布特性,根据算例桥梁的抗震设防烈度,将所选取的12条记录的PGA分别调整为0.2g(设计地震)、0.38g(罕遇地震)和0.6g(本文设定的极端罕遇地震)3种地震动水平,对不同水深下的群桩基础模型进行非线性动力时程分析,以研究损伤沿桩身和桥墩的分布特征。从图9已知,各桩的动力响应结果在数值上虽然略有差异,但总体趋势相一致,因此这里以1#角桩为代表,讨论群桩基础在不同地震动水平下的损伤特性。
4.1 损伤状态评估准则
在结构的地震损伤分析中,选取合适的破坏准则至关重要。目前,已有的破坏准则可大体归纳为4类[22]:强度破坏准则、变形破坏准则、能量破坏准则、变形和能量双重破坏准则。对钢筋混凝土结构,变形和能量双重破坏准则是当前公认的更为合理的破坏准则,该准则同时考虑了结构的最大变形效应和累积耗能损伤效应。其中,由Park等[23]所提出的双参数破坏准则最为经典,被广泛应用于钢筋混凝土结构的地震损伤评估。之后,Stone等[24-27]以Park-Ang双参数地震损伤评估模型为基础,分别进行了改进研究。本文采用Stone等提出的Park-Ang改进模型,该模型剔除了Park-Ang评估模型第一项中的可恢复弹性变形,并采用弯矩和曲率指标描述结构的地震响应,适合于群桩基础的损伤判定
(6)


表6 Stone等建议的破坏等级
4.2 群桩基础损伤分布特性
由式(6)可知,滞回耗能是地震过程中结构损伤的重要组成部分,为了揭示耗能沿桩身、墩底的分布特征,以所选用的1979年Imperial Valley地震CA-Array台站近场记录为输入,计算水面位于承台底部(HW=9.54 m)时群桩基础的动力响应。由不同高度处桩截面的滞回曲线可发现,桩顶处较早进入非线性状态并向下扩展,而桩身偏下部位则基本保持弹性状态,限于篇幅这里未列出各截面在不同PGA下的滞回图。图12给出了滞回耗能沿桩基竖向的分布,从图中可看出,3种地震动水平下,墩底(对应的结构高度H=61 m)处滞回耗能最大,在冲刷线以上,滞回耗能从桩顶自上而下逐渐减小,且随着地震动强度的增大,发生塑性耗能的范围相应扩大。当PGA=0.38g时,在冲刷线以下一定深度的两土层(第5层与第6层)交界处,桩身产生塑性耗能,出现一定程度的非线性损伤,并且,随着PGA的增大,塑性损伤逐渐向两端扩展。
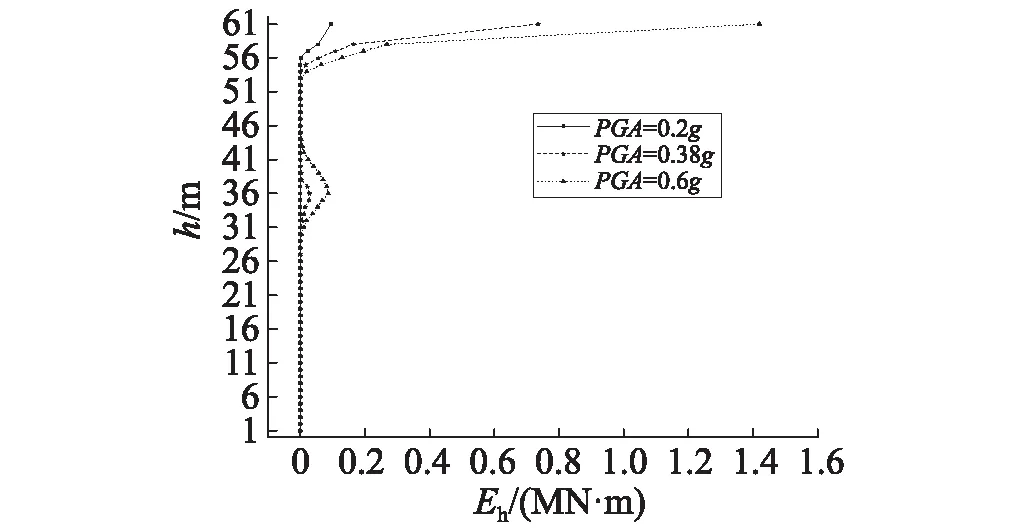
图12 CA-Array近场记录下1#桩及墩底滞回耗能分布Fig.12 Distribution of hysteretic energy along 1# pile and pier bottom under CA-Array record
为了对比近、远场地震下群桩基础的损伤分布特性,将所选取的12条记录的PGA分别调整为前述3种地震动水平开展非线性动力时程分析。图13为水深HW=9.54 m(水面位于承台底部)时损伤均值沿1#桩和墩底高度方向的分布。从图中可看出,不同PGA水平下,近场地震时桩身损伤最严重的部位均在桩顶,冲刷线以下的桩身也可能出现不同程度的损伤。具体的,PGA=0.38g时,最大损伤出现在桩顶,DI=0.19,处于第二破坏等级(0.11~0.4)之间,其损伤状态为“可修复~压溃展开但仍具有固有刚度”。PGA=0.6g时,最大损伤仍然出现在桩顶,此时DI=0.40,处于第二破坏等级(0.11~0.4)之间,其损伤状态也为“可修复~压溃展开但仍具有固有刚度”,但此时损伤开始沿桩身向下扩散。远场地震下,群桩基础主要处于弹性状态,和近场下存在显著差别。

图13 近、远场地震下1#桩和墩底损伤分布Fig.13 Distribution of damage of 1# pile and pier bottom under near-fault and far-field earthquakes
为了讨论水深的影响,图14列出了近场地震下1#桩桩顶在不同PGA水平下损伤均值随水深的分布。可发现,同一PGA水平下,桩顶损伤均随水深增加而有所增大。
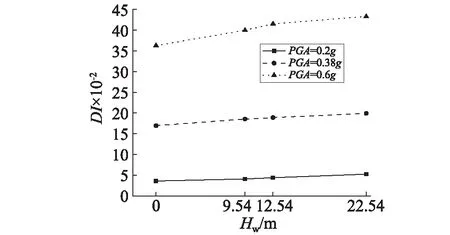
图14 近场地震下1#桩桩顶损伤随水深的分布Fig.14 Distribution of damage of 1# pile top with water depths under near-fault earthquakes
由上述分析可知,近场地震作用下群桩基础的动力响应和损伤水平均明显大于远场,表明脉冲型近场地震动具有更高的变形和耗能需求,应在近断层区深水桥梁的抗震设计中予以重视,尤其应关注高烈度区非线性阶段的延性设计。
5 结 论
通过本文分析,可得到以下结论:
(1)近场地震下群桩基础的动力响应明显大于远场,PGA=0.2g时剪力、弯矩、位移和轴力的最大增幅分别为150.6%、227.2%、333.4%和64.2%,表明脉冲型近断层地震动具有更高的需求,应在深水桥梁的抗震设计中予以重视。
(2)墩底、承台底与桩顶交界处是群桩基础的主要易损部位,近场地震下,其损伤水平随地震动强度增加而增大,随水深增加而略有增大。不同地震动水平下,桩顶分别处于“完好或局部轻微开裂”和“可修复~压溃展开但仍具有固有刚度”状态,且损伤范围不断扩大。远场地震下,群桩基础主要处于弹性状态。
(3)由于桩周土的约束作用,一定深度的土层交界处(本文算例为第5层与第6层土交界附近)也可能出现结构损伤,且损伤程度会随着地震动强度的增加而增大,并向两端扩散,但损伤程度低于桩顶。
(4)“m法”是一种线弹性模拟方法,不能直接用于强震下桩侧土进入非线性状态后的模拟,此时如继续采用“m法”,有可能导致计算结果偏于保守。对比可发现,根据桩侧土体进入非线性程度的不同对m值进行适当修正后,也可以得到较为准确的桩基础动力响应。
[ 1 ] LIAW C Y, CHOPRA A K. Dynamics of towers surrounded by water[J]. Earthquake Engineering and Structural Dynamics, 1974, 3(1): 33-49.
[ 2 ] GOYAL A, CHOPRA A K. Earthquake analysis of intake-outlet towers including tower-water-foundation-soil interaction[J].Earthquake Engineering and Structural Dynamics, 1989,18(3): 325-344.
[ 3 ] KIMURA M, ZHANG F. Seismic evaluation of pile foundation[C]∥Proceeding of 6th International Symposium, Numerical Models in Geomechanics. Montreal: Balkema,1997: 545-548.
[ 4 ] 叶爱君,鲁传安.基于Pushover分析的群桩基础抗震性能分析方法[J].土木工程学报,2010,43(2): 88-94.
YE Aijun, LU Chuan’an. A seismic performance analysis approach based on pushover analysisfor group pile foundations[J]. China Civil Engineering Journal, 2010, 43(2): 88-94.
[ 5 ] 江辉,李杰,杨庆山.考虑SSI 三种效应的桩基础RC 梁式桥抗震性能评估方法研究[J].振动与冲击,2012,31(5): 65-72.
JIANG Hui, LI Jie,YANG Qingshan. A seismic performance evaluation method for a pile-foundation RC girder bridge considering three kinds of SSI effect[J]. Journal of Vibration and Shock,2012,31(5): 65-72.
[ 6 ] 魏凯,伍勇吉,袁万城,等. 桥梁群桩基础-水耦合系统动力特性数值模拟[J].工程力学,2010,28(增刊1): 195-200.
WEI Kai, WU Yongji, YUAN Wancheng, etal. Numerical dynamic analysis for water-pile group bridge foundation interacted system[J].Engineering Mechanics, 2010, 28(Sup1): 195-200.
[ 7 ] 魏凯,袁万城.深水高桩承台基础地震动水效应数值解析混合算法[J].同济大学学报(自然科学版),2013,41(3):336-967.
WEI Kai, YUAN Wancheng. A numerical-analytical mixed method of hydrodynamic effect for deep-water elevated pile cap foundation under earthquake[J]. Journal of Tongji University(Natural Science), 2012, 41(3): 336-967.
[ 8 ] 黄信,李忠献. 动水压力作用对深水桥墩地震响应的影响[J]. 土木工程学报,2011,44(1): 65-73.
HUANG Xin, LI Zhongxian. Influence of hydrodynamic pressure on seismic response of bridge piers in deep water[J]. China Civil Engineering Journal, 2011, 44(1): 65-73.
[ 9 ] 宋波,李悦. 高桩承台动水力简便计算方法[J]. 北京科技大学学报,2011,33(4): 509-514.
SONG Bo,LI Yue. Simplified calculation method of hydrodynamic force for elevated pile caps[J]. Journal of University of Science and Technology Beijing, 2011, 33(4): 509-514.
[10] WEI K, YUAN W C, BOUAANANI N. Experimental and numerical assessment of the three dimensional modal dynamic response of bridge pile foundations submerged in water[J].Journal of Bridge Engineering,2013, 18(10): 1032-1041.
[11] 黄麟,蒋劲松,姚红兵. 庙子坪岷江大桥震后主墩裂缝的成因分析以及深水修复与加固[J]. 西南公路,2008(4): 32-35.
HUANG Lin, JIANG Jingsong, YAO Hongbing. Crack cause analysis for the main pier of Miaoziping Min River bridge after earthquake and repair and reinforcement under deep-water environment[J]. Southwest Highway, 2008(4): 32-35.
[12] 黄信,李忠献. 动水压力作用下深水桥墩非线性地震响应分析[J]. 震灾防御技术,2010,5(3):352-357.
HUANG Xin, LI Zhongxian. Nonlinear seismic response analysis of bridge pier in deep water under hydrodynamic pressure influence[J]. Technology for Earthquake Disaster Prevention, 2010, 5(3): 352-357.
[13] 孙治国,王东升,郭迅,等. 钢筋混凝土墩柱等效塑性铰长度研究[J]. 中国公路学报,2011,24(5):56-64.
SUN Zhiguo, WANG Dongsheng, GUO Xun, et al. Research on equivalent plastic hinge length of reinforced concrete bridge column[J]. China Journal of Highway and Transport, 2011, 24(5) : 56-64.
[14] 杨红,白绍良. 基于变轴力和定轴力试验对比的钢筋混凝土柱恢复力滞回特性研究[J]. 工程力学, 2003, 20(6): 58-64.
YANG Hong, BAI Shaoliang. The hysteretic behavior of RC columns based on the contrasting tests under constant and varying axial forces[J]. Engineering Mechanics, 2003, 20(6): 58-64.
[15] 汪训流,陆新征,叶列平. 变轴力下钢筋混凝土柱的抗震性能分析[J]. 工业建筑, 2007, 37(12): 71-75.
WANG Xunliu, LU Xinzheng, YE Lieping. Analysis of earthquake-resistent behaviors of RC columns under variable axial loads[J]. Industrial Construction, 2007, 37(12): 71-75.
[16] 燕斌,王志强,王君杰. 桥梁桩基础计算中p-y曲线法与m法的对比研究[J]. 结构工程师, 2007, 23(4): 62-68.
YAN Bin, WANG Zhiqiang, WANG Junjie.Study on comparison ofp-ymethod and m-method in computation of bridge pile foundations[J]. Structural Engineers, 2007, 23(4): 62-68.
[17] JIANG H, WANG B X, BAI X Y, et al. Simplified expression of hydrodynamic pressure on deep-water cylindrical bridge piers during earthquakes[J]. Journal of Bridge Engineering, 2017 , 22 (6) :04017014.
[18] MORISON J R, O’BRIEN M P, JOHNSON J W, et al. The force exerted by surface waves on piles[J]. Journal of Petroleum Technology, 1950, 2(5): 149-154.
[19] GOTO H, TOKI K. Vibration characteristics and a seismic design of submerged bridge piers[C]∥Proceedings of the 3rd World Conference on Earthquake Engineering. New Zealand:New Zealand National Committee on Earthquake Engineering, 1965: 107-122.
[20] BHATTA D D, RAHMAN M. On scattering and radiation problem for a cylinder in water of finite depth[J]. International Journal of Engineering Science, 2003,41(9): 931-967.
[21] 王君杰,赖伟,胡世德. 深水高桩基础桥梁地震水动力效应分析[J]. 同济大学学报(自然科学版),2011,39(5): 650-655.
WANG Junjie, LAI Wei, HU Shide. Seismic hydrodynamic effects on group-pile foundations with caps merged in water[J]. Journal of Tongji University(Natural Science), 2011, 39(5) : 650-655.
[22] 庞于涛,袁万城,沈国煜,等. 基于结构易损性分析的公路桥梁可靠度研究[J]. 哈尔滨工程大学学报,2012,33(9):1091-1096.
PANG Yutao, YUAN Wancheng, SHEN Guoyu, et al. Reliability analysis of highway bridges based on structural vulnerability analysis[J]. Journal of Harbin Engineering University, 2012,33(9): 1091-1096.
[23] PARK Y, ANG A H. Mechanistic seismic damage model for reinforced concrete[J]. Journal of Structural Engineering, 1985, 111(4): 722-739.
[24] STONE W C, TAYLOR A W. ISDP: Integrated approach to seismic design of reinforced concrete structures[J]. Journal of Structure Engineering, 1994, 120(12): 3548-3566.
[25] 牛荻涛,任利杰. 改进的钢筋混凝土结构双参数地震破坏模型[J]. 地震工程与工程振动,1996,16(4):44-54.
NIU Ditao, REN Lijie. A modified seismic damage model with double variables for reinforced concrete structures[J]. Earthquake Engineering and Engineering Vibration,1996, 16(4): 44-54.
[26] 王东升,冯启民,王国新. 考虑低周疲劳寿命的改进Park-Ang地震6损伤模型[J]. 土木工程学报,2004,37(11):41-49.
WANG Dongsheng, FENG Qimin, WANG Guoxin. Amodified Park-Ang seismic damage model considering low-cycle fatigue life[J]. China Civil Engineering Journal, 2004, 37(11): 41-49.
[27] 江辉,朱晞. 以性能指标为控制变量的强度折减因子[J]. 铁道学报,2008,26 (6): 88-95.
JIANG Hui, ZHU Xi. Strength reduction factor model with performance index as control parameter[J]. Journal of the China Railway Society,2008,26(6): 88-95.

