一种新型TBM刀具磨损检测技术
李宏波, 孙振川, 周建军, 张宏伟, 韩雪峰, 喻 伟
(1.盾构及掘进技术国家重点实验室,郑州 450001;2.中铁隧道集团有限公司,河南 洛阳 471009;3.中铁建设投资集团有限公司,广东 深圳 518000)
随着隧道及地下空间工程的大发展,TBM(Tunnel Boring Machine)工法被越来越多的在城市地铁隧道,引水供水隧道,穿江越海隧道,电力电讯及供气工程中使用。TBM也被称为隧道硬岩掘进机,在施工中更多的被应用于硬岩地层,在硬岩地层掘进中,由于岩石强度高,刀具磨损剧烈,加之在隧道施工过程中,地质工况复杂,如未能及时了解刀具磨损信息而对刀具状态做出合理的评估,一旦刀具磨损报废后,刀具更换复杂困难,成本巨大,不但会影响整个工程的质量还会拖延工期。因此,对TBM刀具磨损状态进行检测和有效评估是当前研究的一个热点问题[1-4]。
目前TBM刀具检测多依靠刀具制造商在制造刀具过程中内置的传感器电路或液压油路来完成检测,该检测方法仅当刀具磨损到一定程度,出现内置电路短路或油路泄压后才有效,该方法仅作为一种更换刀具的参考判断,无法评估在掘进过程中刀具的偏磨程度,刀圈磨损等过程状态,本文提出的利用声发射作为检测手段,基于自适应卡尔曼(Kalman)滤波和改进的信息熵值模型多散点多参量的权重融合刀具检测是基于刀具磨损过程的检测[5-9]。
刀具磨损在微观上表现为材料内部细微裂纹的扩展,声发射(Acoustic Emission,AE)技术对裂纹的扩展非常敏感,能够反映出裂纹的早期形成及发展裂化的过程[10-12]。以TBM模态掘进试验台搭载的不同刀具为研究对象,采集声发射多散点信息,提出了一种基于改进的熵值赋权法来融合多特征参量的刀具状态评估模型。声发射信号的多散点及多特征参量的融合有效的消除了单个异常数据样本点的影响。此外在声发射特征输入模型算法评估前,对AE散点采用门槛阈值滤波,对AE波形采用自适应Kalman滤波,以便获取更加真实有效的样本原始信号,文章从刀具试验和模型算法二方面进行研究,将熵权法刀具状态评估值同实际的TBM刀具磨损状态进行比对,从而后续为TBM刀具的现场检修和保养提供指导,文章的整体研究结构框架图如图1所示。
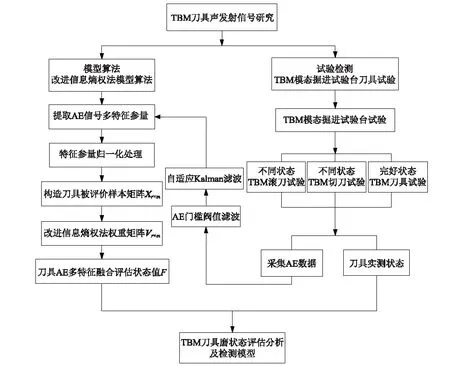
图1 研究框架流程图Fig.1 The study flow diagram
1 基于自适应Kalman滤波的信号处理
Kalman滤波是在平稳及非平稳环境下利用基于状态空间的最佳线性递推方法来实现滤波,自适应Kalman滤波则是在经典Kalman滤波的基础上进行改进,通过己知状态方程和量测方程获得的当前的估计值和观测值。在滤波过程的实现中,自适应Kalman滤波一方面利用观测值修正预测值,同时也对未知的或不确切的系统模型参数和噪声统计参数进行修正,自动调整滤波器参数,以适应信号或噪声未知的或随时间变化的统计特征,从而达到最优的滤波结果[13-15]。自适应Kalman滤波原理图如图2所示。

图2 自适应Kalman滤波Fig.2 Adaptive Kalman filter
z(k)为采集的原始信号k时刻数值,z(k)由能够反映出被测评对象的真实有用信号x(k)和噪声v(k)构成的,x(k)和v(k)不相关。自适应Kalman滤波利用量测数据进行递推滤波时,实时估计和修正系统噪声和量测噪声的统计特性,从而达到降低系统模型误差、抑制滤波器发散提高滤波精度,该滤波的模型如下,假设
xk=Φk, k-1xk-1+wk
(1)
zk=Hkxk+vk
(2)
(3)
通过对滤波器模型参数的实时估计,得出各个参量的估计量为
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
式中,N为滤波器平滑窗口宽度。
2 基于改进信息熵值赋权法状态评估
2.1 改进熵权法模型
熵的概念起源于热力学,又称为平均信息量,表征信息的无序程度,信息熵越大,信息无序度越高,信息效用值越小。信息熵越小,信息的无序度越小,信息的效用值越大,利用熵值法这一特征信息可区分信息的多参量权重层次[16-20]。
传统信息熵值模型仅针对一路被测信号多特征来赋权评估,当被评估预测对象为多组信息时,熵权法无法有效使用。由于声发射信号的特殊性,每次数据采集可以得到多个声发射散点,每个AE散点均可看成一组完整信息,每个散点均均包含多个特征信息参量。并且每个AE散点包含的故障信息不同,对评估对象的状态信息贡献度也不同。此外,还考虑到多组AE散点中有一些偏离真实状态的异常样本点,因此对传统信息熵权法模型进行改进,将被评估对象的多个数据样本点和其对应的多个特征信息参量进行融合,提出了一种基于声发射信号的多散点多特征融合的熵权法模型算法,该算法模型可有效的对AE多特征参量进行融合,且消除AE异常样本点的影响。现将该模型算法介绍如下。
传统的信息熵模型可简单表示为在一个信息通道中传输的第i个信号的信息量Ii
Ii=-lnpi
(12)
式中,pi为该信号出现的概率,如果有n个信号,其出现的概率分别为p1,p2, …,pn,那么这n个信号的平均信息量即熵
(13)
改进熵权法AE信号评估则针对多组信号,多特征参量进行融合,假设被测评对象为n,每个测评对象包含r个数据样本,构造测评向量{p1,p2, …,pn},数据样本向量{Q1,Q2, …,Qr},AE数据样本点Q和特征值T可以组成设备状态评价样本特征矩阵。
(14)
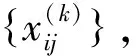
(15)
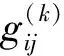
(16)
(17)
(18)
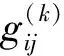
(19)

(20)
2.2 熵权法状态评估
依托TBM模态掘进试验台采集不同刀具的声发射信号,获得声发射信号源,针对声发射多散点和多特征参量构造评价矩阵Xr×m,Xr×m为r个数据样本点,每个样本点对应m个特征值。利用模型算法得出Vr×m赋权矩阵,故声发射的多散点和多特征信号后得出的状态评估数值Fn可以表示为
(21)
式中,Fn作为被评估对象的综合评估值融合了r个声发射事件样本散点和其对应m个特征量,有效的减少了异常AE样本点的影响,剔除异常数据散点的差异。
3 TBM刀具声发射信号实验分析
TBM模态掘进试验台(见图3)是为真实模拟实际TBM掘进施工而设计的硬岩掘进平台,该平台可以搭载不同的TBM刀具,模拟不同状态的刀具破岩机理,TBM模态掘进试验台岩石箱体是固定的,电机通过减速器、安全轴、小齿轮、大齿圈、主轴承各个部件带动刀盘旋转和刀盘推进。实验平台的额定扭矩和加载推力大,能够真实反映出硬岩掘进施工TBM的状态信息。为了验证基于自适应Kalman滤波和改进的信息熵值模型多散点多参量的权重融合方法可清晰有效的反映出刀具的不同磨损状态,以TBM模态掘进试验台搭载的不同刀具为研究对象进行刀具声发射信号采集。

图3 TBM模态掘进试验台Fig.3 TBM mode driving test bench
3.1 试验设计及参数设置
为了验证该模型评估算法的有效性以期对实际TBM刀具磨损状态进行有效的评估和检测。考虑到试验的比对效果,设计3组试验分别对不同磨损状态的TBM滚刀状态进行评估检测、对不同磨损状态的TBM切刀状态进行评估检测、对完好状态的不同TBM刀具进行状态评估检测。通过在刀箱中安装不同磨损状态的刀具,搭载声发射数据采集设备采集TBM刀具破岩声发射信号。在TBM掘进试验台上设置好设备参数,为了有所比对,每次测试设备参数保持一致。特别需要说明的是,由于试验均是单刀进行破岩,刀具承受的载荷很大,推进速度不宜过快。在破岩掘进过程中,TBM模态掘进试验台设备参数设置如表1所示。

表1 TBM模态试验台掘进参数
检测系统采用美国PAC的多通道声发射数据采集系统进行数据采集,通过磁力座将声发射传感器固定在刀箱上。在声发射数据采集设备中设置好采集参数,进行AE数据采集。连续采集240 s的声发射信号。然后更换刀具,按照相同的步骤依次采集其它刀具的声发射信号,AE设备采集参数如表2所示。

表2 采集参数
3.2 数据处理及结果分析
每次试验对刀具破岩的声发射信号进行采集,作为一次状态评估样本,采集到的声发射散点信号如图4所示,图中每个声发射散点均为一个完整的AE波形信号,相应的每个散点均可以提取声发射多个特征参量。
试验提取声发射信号的12个特征参量:上升时间、持续时间、信号强度、RMS(Root Mean Square)、幅值、峰频、平均频率、ASL(Automatic Shift Lock)、峰值频率、能量、绝对能量、中心频率。提取声发射特征参量前,为了被测试对象的状态评估的准确性,需要尽可能的减少噪声等干扰信号的影响。采取了二次滤波处理方法,一次滤波是通过在声发射数据采集时门槛阈值进行滤波,通过环境背景噪声的测试,设置门槛阈值为35 db,即AE散点在该门槛阈值以下的信号直接去除。二次滤波则是采用自适应Kalman滤波降噪处理方法,该滤波算法特别适应信号随时间变化的统计特征,如图5所示,可以看出通过滤波后去除了干扰信号,声发射信号的峰值等特征信息更加明显。
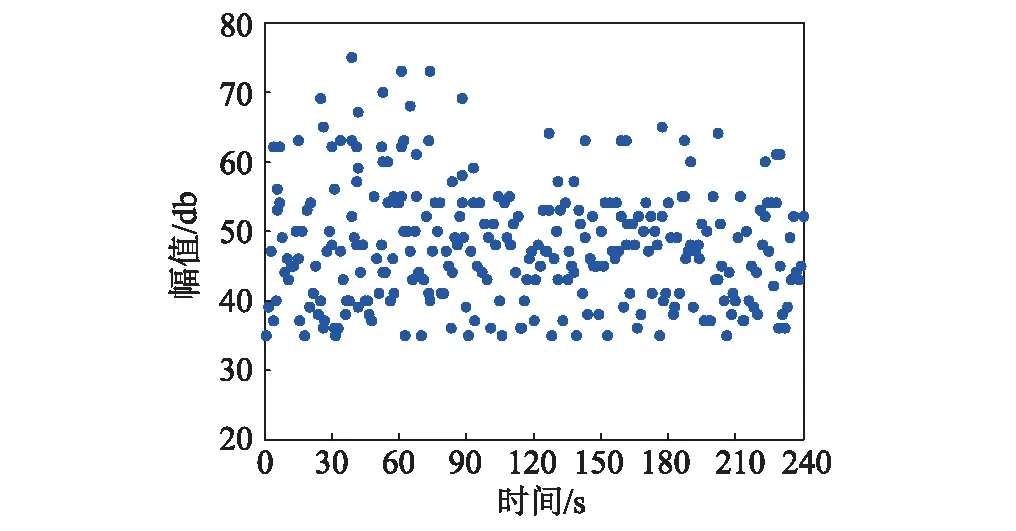
图4 AE散点图Fig.4 AE scatter diagram
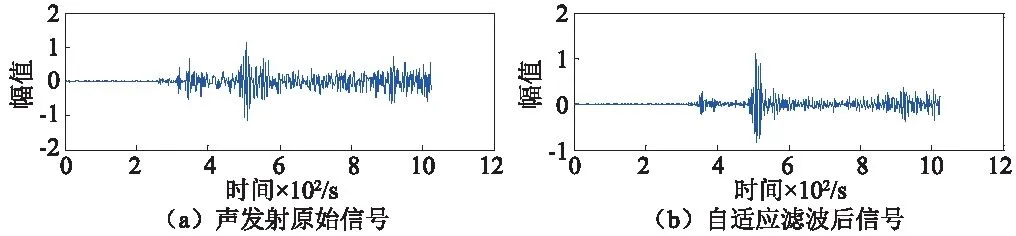
图5 自适应Kalamn滤波Fig.5 Adaptive Kalman filter
针对不同磨损状态的滚刀破岩实验,现有从施工现场得到的处于磨损或报废状态的单刃17英寸滚刀共5把,完好状态的滚刀1把。分别将这些不同磨损状态的滚刀安装在刀箱上,采集AE信号,通过自适应Kalman滤波和改进的信息熵值模型多散点多参量的权重融合后得到评估结果如表3所示。
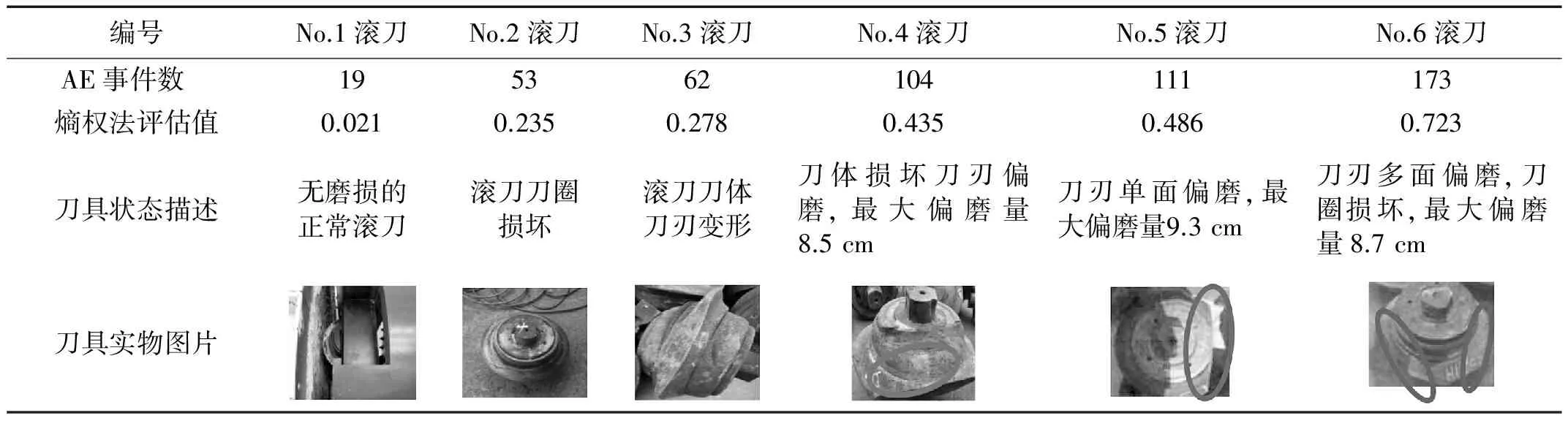
表3 不同磨损状态滚刀模型评估检测
通过表3发现不同磨损状态的滚刀在测试过程中产生的AE事件是不同的,本文提出的模型在有效滤波的前提下,最大限度的利用了AE散点数据,区分了每个事件的特征参量的权重,通过多散点,多特征参量的融合,综合考虑每个AE散点和其对应的特征量的作用,该方法不仅可以消除偏差大的异常点的影响,而且在赋权过程中,突出了重要特征参数的赋权数值,进而准确反映出滚刀的磨损劣化趋势及不同磨损状态的滚刀状态,整个滚刀磨损的趋势图如图6所示。
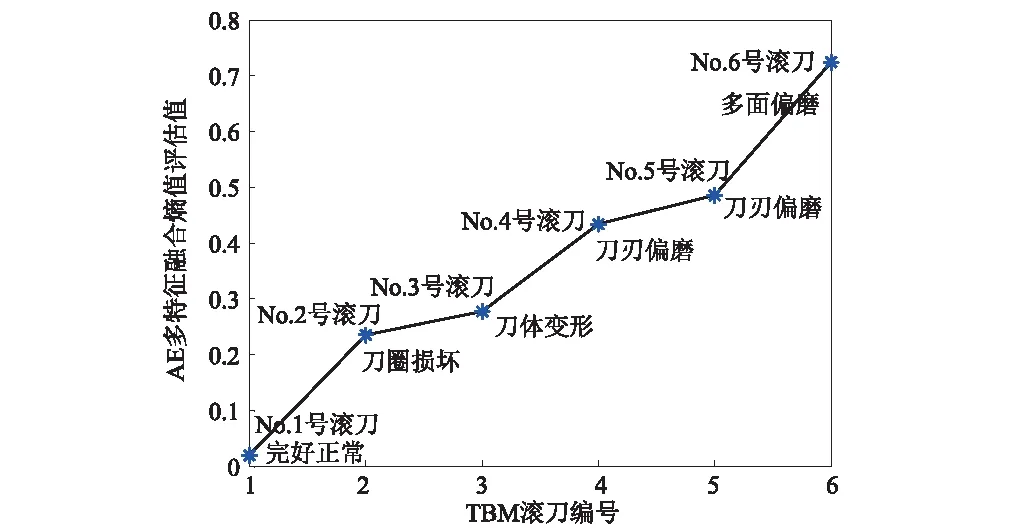
图6 不同状态滚刀状态评估检测值Fig.6 Different hob evaluation values
此外,通过表3中No.5滚刀和No.6滚刀的对比分析,发现如果单一采用磨损量来评估检测滚刀磨损状态,No.5滚刀的最大磨损量为9.3 cm,No.6滚刀最大磨损量为8.7 cm。No.5滚刀的损坏程度应该更加严重,但是No.6滚刀实际中发生了多面偏磨,损坏程度更为剧烈,通过熵权法评估值可以将其有效的区分。
为了进一步验证该评估模型算法对其它刀具的有效性,针对不同磨损状态的切刀开展破岩实验,目前现有施工现场收集的故障切刀2把,完好状态的切刀1把,通过该评估算法得出的结果如表4所示。
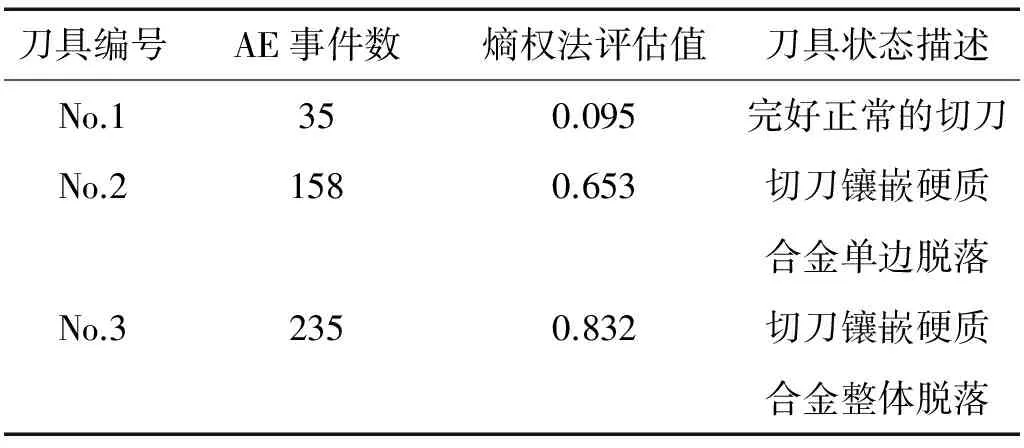
表4 不同磨损状态切刀模型评估检测
局限于切刀的样本少,本次实验仅取了3把刀具进行试验。区别于滚刀的滚压破岩,切刀在与岩石相同接触后更多的是嵌入后的撕裂,因此在相同的35 db门槛阈值滤波下,产生的AE事件更多,但是通过AE多散点多特征融合后依然能够反映出切刀的故障程度和劣化趋势,趋势如图7所示。后续研究过程中需要进一步的积累不同损伤程度的切刀样本来增加试验的可靠性。
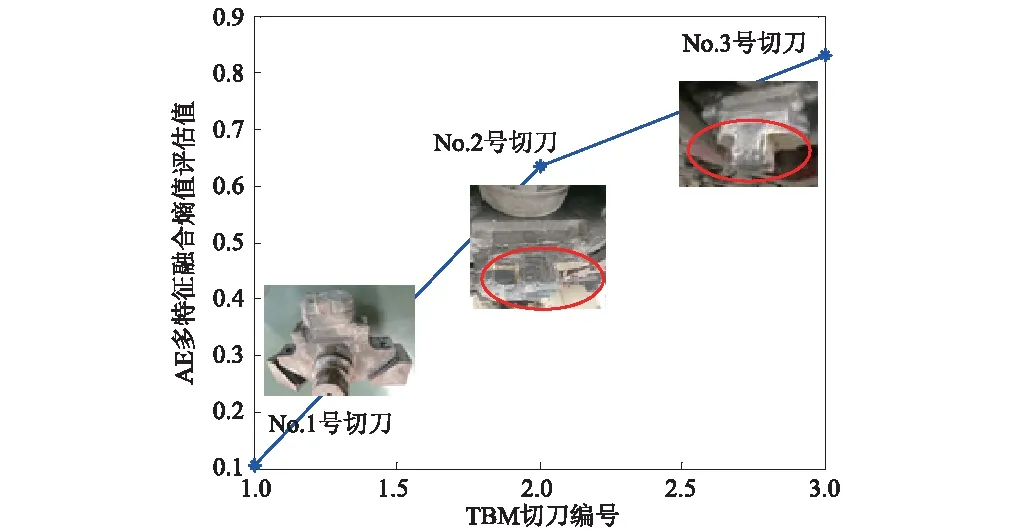
图7 不同状态切刀状态评估检测值Fig.7 Different cutter evaluation values
为了更进一步的验证该模型的通用性,结合本文提出的刀具检测技术,对完好的不同的刀具进行状态检测评估。试验采用17英寸滚刀、19英寸滚刀及双刃滚刀进行试验。试验结果如表5所示。

表5 不同刀具模型评估检测
通过表5发现,如果是正常状态的刀具通过该方法后得到的综合评估值都相对较小,该数值可以作为正常刀具检测的初始数值,即刀具没有磨损的原始状态。
基于自适应Kalman滤波和改进的信息熵值模型多散点多参量的权重融合刀具检测的最终的目的是利用该刀具检测方法,将TBM上配置的不同的刀具实际磨损状态同该熵权法评估值在区间上进行对应,然后同实际的刀具磨损图片进行对应,以便对整个刀具的状态有直观的了解。后续需要针对更多的不同的刀具磨损故障样本进行研究,建立熵权法评估数值同刀具磨损样本的区间对应关系,进而为TBM刀具现场检修和保养提供指导。
4 结 论
(1)利用声发射信号的多散点多特征信息,将声发射技术应用于TBM刀具检测领域,利用自适应卡尔曼滤波对声发射信号进行滤波处理,排除噪声等干扰信号,在此基础上提取声发射信号的多特征信息,保证了信号处理的真实有效性,为声发射信号的后期处理奠定基础。
(2)提出了一种基于改进信息熵值赋权状态评估新方法,该方法综合考虑了声发射数据样本点的差异和多特征值的影响,对多个数据样本点对应的多个特征值进行赋权,强化了对状态评估贡献度大的特征值赋权,突出关键特征参量的作用,消除了偏差较大异常样本点的影响,该方法能够有效的区分和评估TBM刀具的磨损状态。基于改进的信息熵值模型多散点多参量的权重融合刀具检测技术可为现场TBM刀具的检维和保养提供数据参考。
[ 1 ] MBA, ALFAYEZ. Detection of incipient cavitationand determination of the best efficiency point forcentrifugal pumps using acoustic emission[J]. Journal of Mechanical Process Engineering, 2013, 25(9/10): 342-343.
[ 2 ] NEILL, REUBEN. Detection of recirculation in pumps using acoustic emission[C]∥ Comadem. Monash: Monash University, 1998.
[ 3 ] 宗源,张梦.基于趋势分析的AMDF基音检测改进算法[J].振动与冲击,2014, 33(20): 35-38.
ZONG Yuan,ZHANG Meng.Modified ADMF pitch detection algorithm based on trend analysis[J].Journal of Vibration and Shock, 2014, 33(20): 35-38.
[ 4 ] 孙金山,陈明.TBM滚刀破岩过程影响因素数值模拟研究[J].岩土力学,2011, 32(6): 1892-1897.
SUN Jinshan,CHEN Ming. Numerical simulaition of influence factors for rock fragmentation by TBM cutters[J]. Rock and Soil Mechanics, 2011, 32(6): 1892-1897.
[ 5 ] TOUTOUNTZAKIS T, MBA D.Observations of acoustic emission activity during gear defect diagnosis[J].NDT&E International, 2003, 36(7): 471-477.
[ 6 ] MIETTINEN J,ANDERSSON P. Methods to monitor the running situation of grease . lubricated rolling bearings[J]. Lubricated Rolling Bearings, 2015: 92-101.
[ 7 ] TAN C K, MBA. Identification of the acoustic emission source during a comparative study on diagnosis of a spur gearbox[J]. Tribology International, 2005, 38(5): 469-480.
[ 8 ] 胡晓依.基于滤波器组分解的周期性振动冲击信号解调方法及其应用[J].振动与冲击,2008, 27(8): 132-135.
HU Xiaoyi. Demodulation method and its application of periodic vibration signal based on filter bank decomposition[J]. Journal of Vibration and Shock, 2008, 27(8): 132-135.
[ 9 ] MARTYR A J. Engine testing[M]. Holland: Elsevier, 2007: 170-196.
[10] BARAN G, TSNDA I. A new method for computing Lyapunov exponents[J]. Physics Letters A, 2013, 175(6): 421-427.
[11] 郭瑜,迟毅林.弗德卡曼滤波阶比跟踪解耦新方法[J]. 振动与冲击,2009, 28(7): 66-68.
GUO Yu, CHI Yilin. New decoupling approach for Vold-Kalman-filtering order tracking[J]. Journal of Vibration and Shock, 2009, 28(7): 66-68.
[12] CAO Liangyue. Practical method for determining theminimum embedding dimension of a scalar times ries[J]. Physical D, 1997, 110 (122): 43-50.
[13] ALBANO A M, MUENCH J. SVD and grassberger procaccia algorithm[J]. Physical Review A, 2011, 38: 3017-3026.
[14] ROGERS L M. The application of vibration analysis and acoustic emission source location to on-line condition monitoring of antifriction bearings [J]. Tribology International,2004, 12(2) : 51-59.
[15] ABDULALLH M, AL-GHANDI, MBA. Estimation of bearing defect size with acoustic emission[J].Insight-Non-Destructive Testing and Condition Monitoring, 2004,46(12): 758-761.
[16] TAKEO, YOSHIOKA. A detection of rolling contact subsurface fatigue cracks using acoustic emission technique [J]. Lubrication Engineering, 1993, 49 (4) : 303-308.
[17] TAKENS F. Detecting strange attractors in turbulence[J]. Lecture Notes in Math, 1981, 898: 366-381.
[18] KIM H S, EYKHOLT R, SALAS J D. Nonlinear dynamics,delay times, and embedding windows[J]. Physica D, 2009, 127(1/2): 48-59.
[19] SATOSHI O D A. Acoustic emission of bending fatigue process of super-carburised spur gear teeth[J]. Progress in Acoustic Emission XI, 1992, 89: 304-310.
[20] MIYACHIKA K, ODA S, KOIDE T. Acoustic emission of bending fatigue process of spur gear teeth [J]. Journal of Acoustic Emission, 2005, 58: 47-53.

