波形钢腹板PC组合箱梁桥的挠度计算与分析

冀 伟， 蔺鹏臻， 刘世忠

(兰州交通大学土木工程学院，甘肃兰州730070)

波形钢腹板PC箱梁桥是一种新型的钢-混组合结构桥梁.该桥型与传统的混凝土箱梁桥相比可以减轻梁体自重，提高预应力的施加效率［1］，因而已在国内外的桥梁建设中得到了广泛的应用.

波形钢腹板PC箱梁桥在竖向荷载作用下，波形钢腹板承担了全部剪力，其产生的剪切变形对波形钢腹板PC箱梁桥的挠度有较大影响.国内外众多学者已对波形钢腹板的剪切性能进行了研究:SAMANTA等研究了波形钢腹板有效剪切模量的取值［2］;YI、ELDIB 及 HASSANEIN 等［3-5］研究了波形钢腹板的剪切屈曲强度;K ESDI等对波形钢腹板在剪切力作用下引起的翼板附加横向弯矩进行了研究［6］;李宏江等分析了波形钢腹板的剪切变形对波形钢腹板混凝土简支箱梁桥挠度的影响程度［7］;聂建国等建立了可考虑钢腹板剪切变形梁的理论模型，推导了端部无约束和有约束条件下波形钢腹板简支箱梁桥在均布加载和集中加载下的解析解［8］，随后依据变形等效原理，通过引入重要的影响参数对波形钢腹板梁变形的解析解进一步简化，提出了波形钢腹板梁变形的简化计算方法——有效刚度法［9］;李明鸿等在考虑波形钢腹板剪切变形影响下，推出了波形钢腹板混凝土组合梁的挠曲线初参数方程，并分析了波形钢腹板混凝土简支箱梁桥在多种加载形式下的挠度［10］.

波形钢腹板PC箱梁属于薄壁箱梁构件，其剪力滞效应会降低上、下混凝土翼板的弯曲刚度［11］，会对结构的挠度造成一定的影响.在特定的宽跨比和特定的波形钢腹板截面高度下，箱梁剪力滞效应对结构挠度的影响也不可忽略.文献［12］在考虑箱梁剪力滞和钢腹板剪切变形影响下，运用能量变分法推导出了波形钢腹板PC简支箱梁的挠度计算公式，但是在分析剪力滞效应时选择了普通箱梁桥剪力滞效应的翘曲位移函数，影响了波形钢腹板PC箱梁这一特殊结构剪力滞效应分析理论的严密性.

针对研究现状和存在的问题，本文从波形钢腹板PC箱梁剪力滞产生的本质即混凝土上、下翼板的面内剪切变形和弯曲剪力流的分布规律出发，并以“拟平截面假定”为变形协调条件［13］，在理论上推导可同时考虑箱梁剪力滞效应和波形钢腹板剪切变形的波形钢腹板PC箱梁桥特有的纵向位移函数，并运用能量变分原理，以所得的纵向位移函数为基础，推出了该桥型的挠度计算公式.计算公式的正确性得到了有限元和室内模型试验的验证，从而为该桥型的挠度计算和分析提供科学合理的理论依据.

1 波形钢腹板PC箱梁桥挠度计算公式推导

在任意的竖向荷载作用下，波形钢腹板PC箱梁桥的挠度W会受到箱梁剪力滞效应(如图1所示)及波形钢腹板剪切变形的影响(如图2所示).

图1 波形钢腹板PC箱梁的剪力滞效应Fig.1 Shear lag effect in a box girder with CSWs

在波形钢腹板剪切变形的影响下，其挠曲线上任一点斜率，包含由弯矩引起的曲率y和波形钢腹板剪切变形γs.

图1中:σx为考虑剪力滞效应的正应力;

珚σx为初等梁理论计算的正应力;

ht为箱梁上翼板中心到截面中性轴的距离;

hb为箱梁下翼板中心到截面中性轴的距离;

hw为波形钢腹板的高度;

b为箱梁顶板宽度;

a为箱梁翼缘板宽度，a=ζb，其中ζ为系数.

图2 波形钢腹板PC箱梁在x-z平面内的剪切变形Fig.2 Shear deformation in a box girder with CSWs in x-z plane

1.1 波形钢腹板PC箱梁纵向位移函数的推导

薄壁箱梁的剪力滞效应是翼板的面内剪切变形引起的正应力沿翼板宽度的非均匀分布现象［14］，因此可以从混凝土上、下翼板的面内剪切变形规律出发来定义波形钢腹板PC箱梁的剪力滞翘曲位移函数.对于图1所示的波形钢腹PC箱梁截面，可以在箱梁顶、底板任意位置虚构一个切口，使之成为开口断面，此时由竖向剪力Q引起的弯曲剪力流q的计算公式为［15］

式中:Iy为波形钢腹板PC箱梁对y轴的截面惯性矩;

t为翼板的壁厚.

以顶板的弯曲剪力流计算为例，若周线坐标s的原点选在顶板中心处，则由式(1)可得

设u为顶板的纵向位移，顶板的面内剪切变形为

式中:Gc为混凝土的剪切模量.

对式(3)进行积分可得

式中:u0为顶板中心处的纵向位移.

由式(4)可得顶板与波形钢腹板交界处的纵向位移为

由式(6)可得箱梁顶板的最大纵向位移差函数为

利用顶板的纵向位移边界条件:当y=0时，u=u0;当y=b时，u=u1，可得箱梁顶板考虑剪力滞效应的纵向位移函数为

同理可得波形钢腹板PC箱梁的悬臂板和底板的纵向位移函数 ux(x，y，z)和 ub(x，y，z).

波形钢腹板PC箱梁纵向弯曲受力时，其横截面的“拟平截面假定”成立，在波形钢腹板和上、下混凝土翼板交界处的1、2位置的纵向位移可表达为式(10)和(11)，式中考虑了波形钢腹板的剪切变形影响.

式中:f(x，z)为理论上推导所得适用于波形钢腹板PC箱梁桥的剪力滞翘曲位移函数.

1.2 能量法推导挠度计算公式

波形钢腹板PC箱梁的顶板、悬臂板和底板沿纵向的正应变和横向的剪应变如式(14)、(15)所示［15］.

顶板、悬臂板和底板的应变能为

波形钢腹板的剪切应变能为

式中:As为波形钢腹板有效剪切面积;

Gs为波形钢腹板的有限剪切模量，计算方法详见文献［2］.

波形钢腹板PC箱梁桥的外力势能珚W为

由最小势能原理可知，体系总势能的一阶变分为0，即

对式(19)～(21)变换整理后可得式(23)～(24)

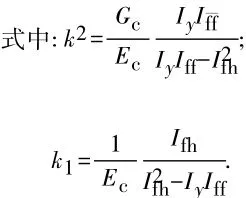
对式(23)进行两次积分运算后便可得到波形钢腹板PC箱梁桥的挠度计算公式为

式中:

2 算 例

2.1 均布荷载作用下波形钢腹板PC简支箱梁桥的挠度

如图3所示，在均布荷载q作用下的波形钢腹板PC简支箱梁桥，距离坐标原点任意位置x处的剪力和弯矩分别为

图3 均布荷载作用下的波形钢腹板PC简支箱梁桥Fig.3 Simply supported girder under a uniform load

由文中第2部分的推导可得其挠度计算公式为

2.2 均布荷载作用下波形钢腹板PC连续箱梁桥的挠度

如图4所示的在均布荷载q作用下的波形钢腹板PC两跨连续箱梁桥，距离坐标原点任意位置x处的剪力和弯矩分别为

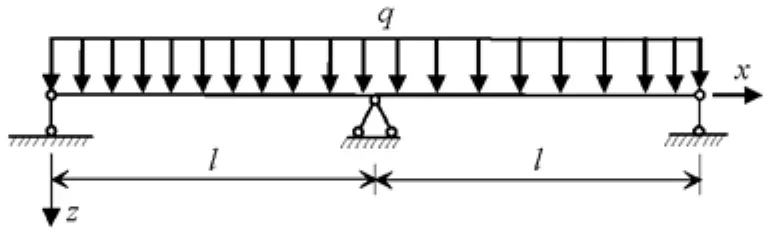
图4 波形钢腹板PC连续箱梁桥承受均布荷载作用示意图Fig.4 Continuous box girder under uniform load

则由文中第2部分的推导可得其挠度计算公式为

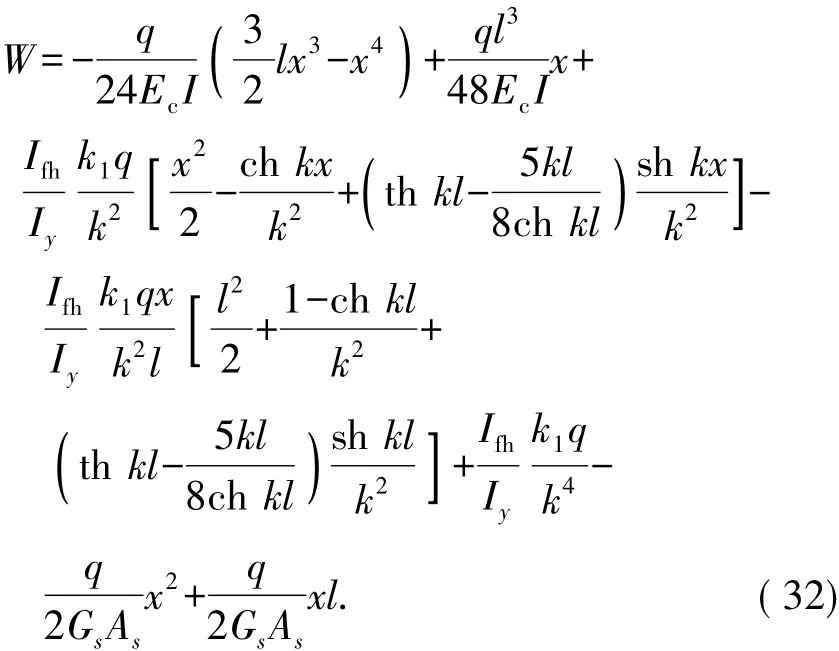
2.3 集中荷载作用下波形钢腹板PC连续箱梁桥的挠度

如图5所示，波形钢腹板两跨连续箱梁桥承受跨中集中荷载P，以左跨为研究对象，其弯矩与剪力方程为分段函数

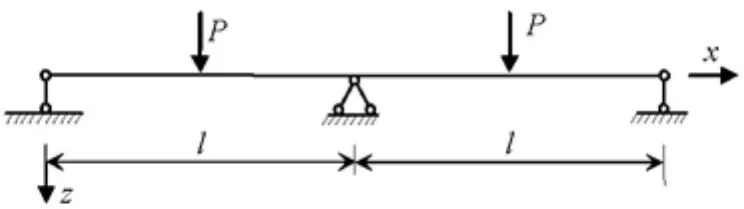
图5 波形钢腹板两跨连续箱梁桥承受集中荷载作用示意图Fig.5 Continuous box girder under concentrated load

则由文中第2部分的推导可得其挠度计算公

3 模型试验

为验证本文所得的求解波形钢腹板PC箱梁桥挠度计算公式的正确性，以所建成的波形钢腹板PC连续箱梁桥-山东省鄄城黄河公路大桥的跨中横截面尺寸为依据，按1∶10缩尺(如图6所示)制作了6 m等截面波形钢腹板PC简支箱梁桥和3+3 m等截面波形钢腹板PC连续箱梁桥的模型试验梁.试验梁的上、下翼板采用C50混凝土，波形钢腹板采用Q235钢，型号为1600型.

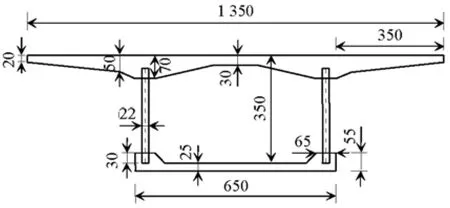
图6 模型梁的横截面尺寸Fig.6 Cross section dimensions of model girder

3.1 模型试验梁的加载工况

(1)波形钢腹板PC简支箱梁桥和连续箱梁桥的均布荷载加载工况

首先在试验梁顶板与波形钢腹板交界处沿桥梁纵向铺设两列方砖，如图7(a)所示，然后在方砖上方沿试验梁中心线对称满铺钢板(钢板重量与预压方砖重量相同，用以消除结构非弹性变形的影响)，随后在钢板上方整齐均匀铺设方砖来近似模拟均布加载，均布加载分为 1.2、2.4、3.6 t 3 个等级进行，挠度测点布置于跨中截面.

(2)波形钢腹板PC连续箱梁桥的集中荷载加载

在波形钢腹板PC连续箱梁桥的跨中截面顶板与腹板交界处放置4个直径为100 mm的钢制圆形分载器来进行集中荷载加载，如图7(b)所示.采用圆钢管架设的支撑体系放置于分载器上，随后在支撑体系上放置形状统一、重量均匀的沙袋近似模拟集中加载，集中荷载加载分为 0.5、1、1.5 t 3 级等级进行.

图7 试验梁加载Fig.7 Test beam loading

3.2 波形钢腹板PC箱梁桥的有限元模型

采用ANSYS 14.0有限元软件建立了波形钢腹板PC箱梁桥的有限元模型，如图8所示.

图8 波形钢腹板PC箱梁桥的有限元模型Fig.8 FEM of the PC box girder bridge with CSWs

4 结果分析对比

运用本文所得的计算公式求得波形钢腹板PC简支箱梁桥及连续箱梁桥在不同荷载类型作用下跨中截面的挠度值，并与有限元值及实测值进行对比，对比结果如图9～10所示.

由图9～10可知，计算值、实测值及有限元值三者吻合良好，验证了本文计算公式的可靠性.

4.1 剪力滞及钢腹板剪切变形随宽跨比变化分别对挠度的影响

假定波形钢腹板的截面高度不变，波形钢腹板PC箱梁桥的跨径l分别取为1～6 m(1的整数倍)，对应实桥的跨径为10～60 m，宽跨比(2b/l)为0.650～0.108.以总挠度 W 为分母，以式(37)考虑剪力滞效应对总挠度的影响和式(38)考虑波形钢腹板剪切变形对总挠度的影响，分析在宽跨比变化时两者对波形钢腹板PC箱梁桥挠度的影响程度.

图9 均布荷载下波形钢腹板PC简支、连续箱梁桥跨中截面挠度Fig.9 Mid-span cross section deflections of simply supported and continuous box girder bridge with CSWs under a uniform load

图10 集中加载下波形钢腹板PC连续箱梁桥跨中截面挠度Fig.10 Mid-span cross section deflections of a continuous box girder bridge with CSWs under a concentrated load

(1)均布荷载作用下的波形钢腹板PC简支箱梁桥

在均布荷载作用下，求得了波形钢腹板PC简支箱梁桥的剪力滞效应(Ja1)和波形钢腹板剪切变形(Jb1)随宽跨比变化对跨中挠度的影响程度，所得结果如图11所示.

由图11可以看出，波形钢腹板PC简支箱梁桥承受均布荷载，在宽跨比范围为 0.108～0.650时，剪力滞效应对其跨中挠度影响较小，而波形钢腹板剪切变形对其跨中挠度影响显著.

(2)均布荷载作用下波形钢腹板PC连续箱梁桥

在均布荷载作用下，求得了波形钢腹板PC连续箱梁桥的剪力滞效应(Ja2)和波形钢腹板剪切变形(Jb2)随宽跨比变化对跨中挠度的影响程度，所得结果如图12所示.

图11 Ja1、Jb1随宽跨比变化示意图Fig.11 Ja1、Jb1varies with the width-span ratio variation

由图12可知:当宽跨比超过 0.650时，剪力滞效应对波形钢腹板PC连续箱梁桥跨中挠度的影响会超过5%;当宽跨比在 0.108～0.650 范围内，波形钢腹板剪切变形对跨中挠度的影响显著.

(3)集中荷载作用下波形钢腹板PC连续箱梁

在集中荷载作用下，求得了波形钢腹板PC连续箱梁桥的剪力滞效应(Ja3)和波形钢腹板剪切变形(Jb3)随宽跨比变化对跨中挠度的影响程度，所得结果如图13所示.

图12 Ja2、Jb2随宽跨比变化示意图Fig.12 Ja2、Jb2varies with the wideth-span ratio variation

图13 Ja3、Jb3随宽跨比变化示意图Fig.13 Ja3、Jb3varies with the width-span ratio variation

由图13可以看出，在集中加载时，箱梁的剪力滞效应要大于均布加载时的剪力滞效应，由剪力滞效应引起的挠度也要大于均布加载的情况.因此，当宽跨比在0.108～0.650范围内时，剪力滞效应和波形钢腹板剪切变形对波形钢腹板PC连续箱梁桥跨中挠度的影响均较大.

由图11～13还可以看出，在集中荷载和均布荷载作用下，剪力滞效应和波形钢腹板剪切变形对波形钢腹板PC箱梁桥(简支和连续体系)跨中挠度的影响程度均随宽跨比的减小而减小.

4.2 剪力滞及钢腹板剪切变形随腹板高度变化分别对挠度的影响

假定波形钢腹板的高度取50～350 mm(50的整数倍)，在宽跨比 0.108～0.650范围内，计算了波形钢腹板PC箱梁桥在不同荷载类型加载下剪力滞效应及波形钢腹板剪切变形分别对其跨中挠度的影响程度，如图14～16所示.

图14 Ja1、Jb1随波形钢腹板高度变化示意图Fig.14 Ja1、Jb1varies with different height of CSWs

(1)均布荷载作用下波形钢腹板PC简支箱梁桥

由图14可以看出，在均布荷载作用时，在同样的宽跨比下，剪力滞效应和波形钢腹板剪切变形随波形钢腹板高度的变化对波形钢腹板PC简支箱梁桥跨中截面挠度的影响较小，尤其是当波形钢腹板高度较低时，两者对跨中挠度的影响基本无变化.当 2b/l=0.650 且 hw/l＜0.2 时，剪力滞效应的影响超过工程允许值的5%.

图15 Ja2、Jb2随波形钢腹板高度变化示意图Fig.15 Ja1、Jb1varies with different height of CSWs

(2)均布荷载作用下波形钢腹板PC连续箱梁桥

由图15可以看出，在均布荷载作用时，在同样宽跨比下，剪力滞效应和波形钢腹板剪切变形随波形钢腹板高度的变化对波形钢腹板PC连续箱梁桥跨中截面挠度的影响较小.当2b/l=0.650且hw/l＜0.25 和 2b/l=0.325 且 hw/l＜0.1 时，剪力滞效应对挠度的影响会超过工程允许值的5%.

(3)集中荷载作用下波形钢腹板PC连续箱梁

由图16可以看出，当宽跨比为 0.108～0.650时，在集中加载时，箱梁的剪力滞效应大于均布加载时的剪力滞效应，剪力滞效应引起的挠度大于均布加载的情况，这时剪力滞效应和波形钢腹板的剪切变形对集中荷载作用下的波形钢腹板PC连续箱梁桥跨中挠度的影响均超过工程允许值的5%.

由图14～16可以看出，波形钢腹板PC连续箱梁桥在集中力作用下跨中截面处的剪力会发生突变，突变的方向与集中力的作用方向一致，剪力突变幅度等于外力的大小，由此引起的剪力滞效应和剪切变形较为明显.波形钢腹板PC连续箱梁桥在均布荷载作用下，其对应区间的剪力图为斜直线，斜线的斜率等于均布荷载的集度，剪力在区间内无突变，引起的剪力滞效应和剪切变形相对于集中荷载作用时小.

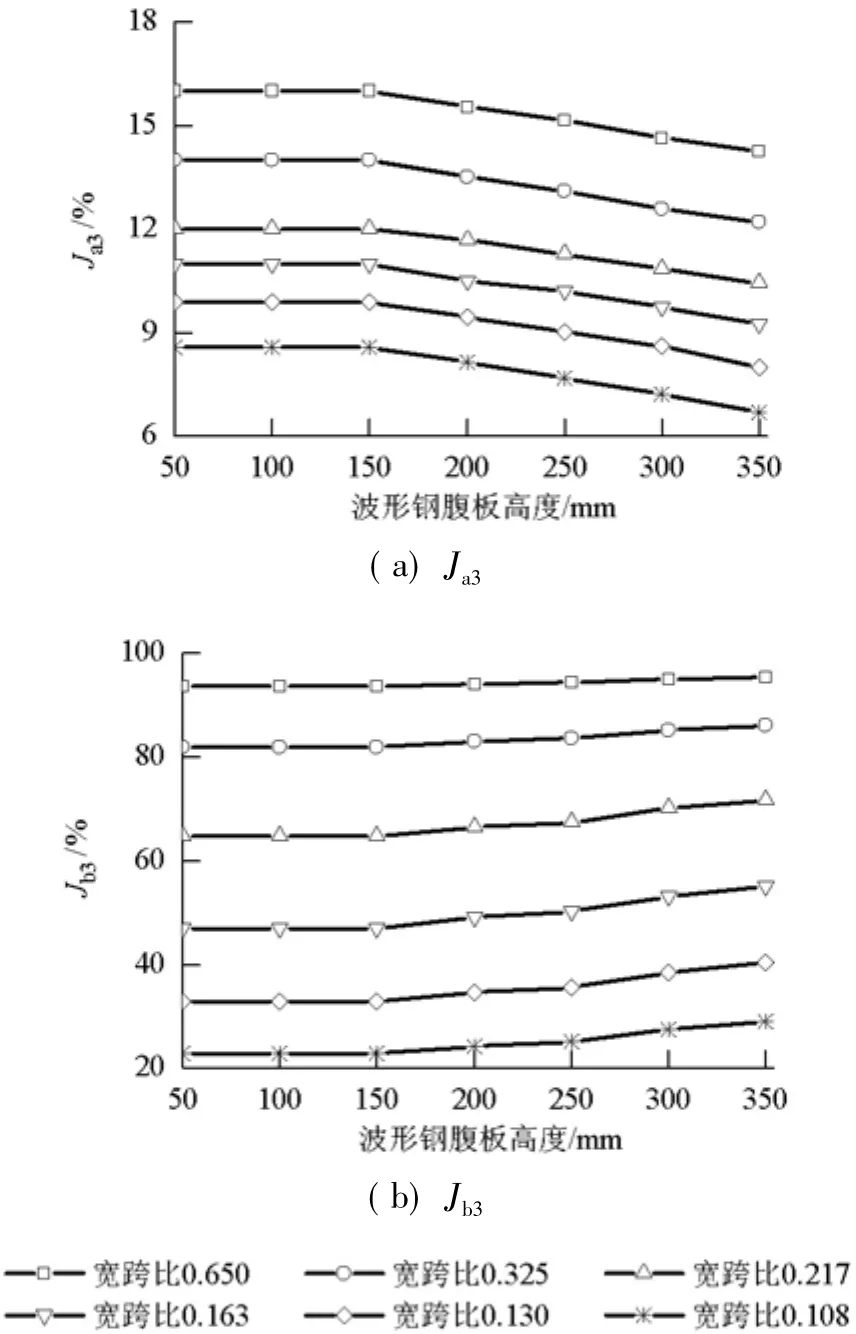
图16 Ja3、Jb3随波形钢腹板高度变化示意图Fig.16 Ja3、Jb3varies with different height of CSWs

5 结论

通过本文的推导分析，可得如下结论:

(1)本文运用能量变分法，在考虑箱梁剪力滞效应和钢腹板剪切变形的基础上，推导出了波形钢腹板PC箱梁桥的挠度计算公式，计算公式的精确度高，可以用于实际工程中此类型桥梁的挠度计算.

(2)在集中荷载和均布荷载作用下，剪力滞效应和波形钢腹板剪切变形对波形钢腹板PC箱梁桥(简支和连续体系)挠度的影响均随着宽跨比的减小而减小.

(3)当波形钢腹板PC箱梁桥的宽跨比恒定，波形钢腹板的高度变化时，剪力滞效应和波形钢腹板剪切变形对波形钢腹板PC箱梁桥挠度的影响较弱，尤其当波形钢腹板高度较小时，两者对该桥型挠度的影响基本无变化.

(4)均布荷载作用下的波形钢腹板PC简支箱梁桥和连续箱梁桥，当宽跨比2b/l=0.108～0.650时，需要考虑波形钢腹板剪切变形对其挠度的影响;当 2b/l=0.650 且当 hw/l＜0.2 时，需要考虑剪力滞效应对波形钢腹板PC简支箱梁桥挠度的影响;当 2b/l=0.650 且 hw/l＜0.25 时和 2b/l=0.325且hw/l＜0.1时，需要考虑剪力滞效应对波形钢腹板PC连续箱梁桥挠度的影响.

(5)集中荷载加载下，当宽跨比2b/l=0.108～0.650时，剪力滞效应和波形钢腹板剪切变形对波形钢腹板PC连续箱梁跨中截面挠度的影响较大，在挠度计算中需要考虑两者对挠度的影响.

致谢:兰州交通大学优秀平台资助(201601).

［1］ 陈宜言.波形钢腹板预应力混凝土桥设计与施工［M］.北京:人民交通出版社，2009:1-12

［2］ SAMANTA A，MUKHOPADHYAY M.Finite element static and dynamic analysesoffolded plates［J］.Engineering Structures，1999，21(3):277-287.

［3］ YI J，GILB H，YOUM K，et al.Interactive shear buckling behavioroftrapezoidally corrugated steel webs［J］.Engineering Structures，2009，30(6):1659-1666.

［4］ ELDIB M.Shear buckling strength and design of curved corrugated steelwebs forbridges［J］.Journalof Constructional Steel Research，2009，65(12):2129-2139.

［5］ HASSANEIN M F，KHAROOB O F.Shear buckling behavior of tapered bridge girders with steel corrugated webs［J］.Engineering Structures，2014，74(9):157-169.

［6］ K ESDI B，JER B，DUNAI L.Bending and shear interaction behavior of girders with trapezoidally corrugated webs［J］.Journal of Constructional Steel Research，2016，121(6):383-397.

［7］ 李宏江，叶见曙，万水，等.剪切变形对波形钢腹板箱梁挠度的影［J］.交通运输工程学报，2002，2(4):17-20.LI Hongjiang，YE Jianshu，WAN Shui，et al.Influence of shear deformation on deflection of box girder with corrugared steelwebs［J］.JournalofTraffic and Transportation Engineering，2002，2(4):17-20.

［8］ 聂建国，李法雄.考虑腹板剪切行为的波形钢腹板梁理论模型［J］.中国公路学报，2011，24(6):40-48.NIE Jianguo，LI Faxiong.Theory model of corrugated steel web girder considering web shear behavior［J］.China JournalofHighway and Transport， 2011，24(6):40-48.

［9］ 聂建国，李法雄，樊健生.波形钢腹板梁变形计算的有效刚度法［J］.工程力学，2012，29(8):71-79.NIE Jianguo，LI Faxiong，FAN Jiansheng.Effective stiffness method for calculating deflection of corrugated web girder［J］.Engineering Mechanics，2012，29(8):71-79.

［10］ 李明鸿，万水，蒋正文，等.波形钢腹板混凝土组合梁挠度计算的初参数法［J］.华南理工大学学报:自然科学版，2015，43(2):66-74.LI Minghong，WAN Shui，JIANG Zhengwen，et al.Initial parameter method for deflection calculation of concrete composite girder with corrugated steel webs［J］.JournalofSouth China University of Technology:Natural Science Edition，2015，43(2):66-74.

［11］ 吴文清，万水，叶见曙，等.波形钢腹板组合箱梁剪力滞效应的空间有限元分析［J］.土木工程学报，2004，37(9):31-36.WU Wenqing，WAN Shui，YE Jianshu，et a1.3-D finite element analysis on shear lag effect in composite box girder with corrugated steel web［J］.China Civil Engineering Journal，2004，37(9):31-36.

［12］ 刘保东，任红伟，李鹏飞.考虑波纹钢腹板箱梁特点的挠度分析［J］.中国铁道科学，2011，32(3):21-26.LIU Baodong，REN Hongwei，LI Pengfei.Deflection analysis considering the characteristics of box girder with corrugated steel webs［J］.China Railway Science，2011，32(3):21-26.

［13］ 吴文清，叶见曙，万 水，等.波形钢腹板-混凝土组合箱梁截面变形的拟平截面假定及其应用研究［J］.工程力学，2005，22(5):177-178.WU Wenqing，YE Jianshu，WAN Shui，et a1.Quasi plane assumption and its application in steel-concrete composite box girders with corrugated steel webs［J］.Engineering Mechanics，2005，22(5):177-178.

［14］ 张元海，白昕，林丽霞.箱形梁剪力滞效应的改进分析方法研究［J］.土木工程学报，2012，45(11):153-158.ZHANG Yuanhai，BAI Xin，LIN Lixia.An improved approach for analyzing shear lag effectofbox girders［J］.China Civil Engineering Journal，2012，45(11):153-158.

［15］ 张士铎，邓小华，王文州.箱形薄壁梁剪力滞效应［M］.北京:人民交通出版社，1998:19-27.