初中数学课堂教学“减负增效”的实践分析

周巧仙

[摘 要] 教师必须弄懂“减负”与“增效”之间的辩证关系，在知识呈现、情境创设、解题教学、作业设计等环节中进行贴合学生实际的考量与权衡，才能使教学做到“加减得法”并因此将“减负增效”真正落到实处.

[关键词] 减负增效；知识呈现；情境创设；过程教学

初中数学教学中的“减负”和“增效”就好比“鱼”和“熊掌”一样都是我们所需要的，但很多教师在实际教学中却往往不能做到两者兼顾. 有的教师过分注重基础知识而令课堂成为教师的“一言堂”，有的教师过于注重基本技能的训练而令数学学习成为机械的“题海战”. 很多教师固执地以为这样的教学是符合落实“双基”的课程要求的，但当前数学教学目标中却又新增了“基本思想”与“基本活动经验”这两大要求，这些教师的教育观念无疑是守旧而落后的.

事实上，数学教育教学改革所追求的目标就包含“减负增效”这一内容，回顾多年课改的历程，数学教学在“减负增效”上所做出的努力、获得的成效也是比较明显的. 不过，学生却仍然无法从内心深处对“数学之美”进行欣赏，有的学生仍然对数学学习存在畏惧心理，数学教师因此在教学中仍然不遗余力地奋斗着. 那么，数学教师在课堂教学中应采取哪些措施来实现真正意义上的“减负增效”呢？

在知识的呈现上减负增效

多年课改确实令我们的数学课堂教学有了巨大的改变，但有的教师在知识的呈现上却仍然不能舍弃新课标已经删除的知识，这种行为势必造成学生学习的负担.

笔者对于此题的求解并没有过于追求效果，但学生却对此题深感兴趣，甚至还有学生提出了这一规律是否适合任何有根的一元二次方程的疑问. 笔者趁机对学生进行了引导，学习尚有余力的学生也在此题的探索中有了更多的收获. 笔者的做法或许比较中庸，但在课堂教学的“加减得当”上也不失为一种良策. 我们数学教师在具体的教学中应把握好课程标准的尺度并将“减负增效”落到实处.

在情境创设上减负增效

教师应经常结合学生实际对教学内容、教学方式等进行新的审视与定位，贴合学生实际需求与认知水平的丰富情境能够更好地唤醒学生的课堂注意力.

例如，圆周角的教材设置中有以下问题情境：某海洋馆的横截面示意图如图1所示，人们观看海洋动物的位置在窗弧AB处，甲位于圆心O处，乙位于窗弧AB正对靠墙的位置C处，甲乙两人的视角∠AOB与∠ACB有何关系呢？假如丙、丁二人分别位于靠墙的位置D与E处，丙丁二人的视角∠ADB，∠AEB与乙的视角是否一样呢？这一情境虽然贴合教学内容，但与学生的生活实际却相当遥远，有的教師进行了海洋馆相关知识的补充以帮助学生理解题意，但这一行为却无形中增加了学生的负担. 有的教师认为这一情境会增加学生负担便将其舍弃，取而代之的是纯粹的讲解，这些行为显然都是比较片面的.

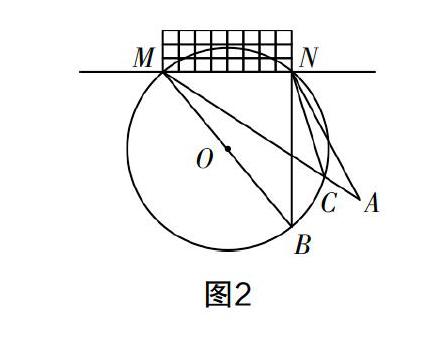
笔者索性对问题进行了重新设计：如图2，甲乙两人在足球比赛中相互配合着向对方球门MN攻去，甲带球至A点时，乙已经跑至B点，这时候甲传球给乙射门还是自己直接射门比较好呢？笔者同时还播放了一个Flash动画以帮助学生理解题意，这一不“加”不“减”的做法令学生的注意力分外集中.

例题、习题上的减负增效

例题教学的处理不当往往会加重学生的负担，史宁中教授就曾强调过数学需要思考这一观点，他认为教师在具体的教学中不应该一味追求熟练，而应该引导学生在不同的尝试中进行探索与归纳，并最终实现思维的突破.

例如，笔者在“配方法解方程”的教学中设计了以下问题串.

问题1：

①x2+14x+______=（x+7）2；

②x2-3x+______=（x-1.5）2；

③x2-9x+______=（x-______）2.

问题2：代数式“x2+10x+______”中应填多少才能令其变为完全平方式呢？

问题3：你在上述问题的解决中可曾发现常数项是与哪一项有联系呢？联系如何？

问题4：请根据自己的发现将式子“x2+px+______”配成完全平方式________.

最后，笔者又请学生思考方程x2-10x+16=0转化为（x+a）2=b时首先应做什么，学生的思路在一个个问题的思考与解决中变得越来越清晰. 笔者以为，教师在具体教学中应围绕教学重难点进行合理的设计，并引导学生不断对问题的本质进行认知与揭示，看似“增加”学生负担的教学设计与行为实际上对学生思维的触动是积极有力的.

作业上的减负增效

很多家长、学生对数学作业往往都会有“浩如烟海”的感觉，数学课堂练习、课后书面作业、周末家庭作业往往让学生苦恼而压抑. “减负增效”的观点一经提出，大家基本上都会将眼光投向“作业”，很多专家、教师在作业的减负增效上也确实投入了很多的精力，教育部门对作业时间不超过1.5小时的要求也是基于这一方面的考虑. 笔者以为，学生作业的布置确实应该得到更多的思考与权衡，合适的权衡与改进才能真正促进学生作业的减负与增效. 学生往往能够在作业中获得更多的基本活动经验并得到不同的发展，因此，作为数学课堂延续的作业环节在数学学习中是不可或缺的. 教师在设计作业时应考虑其实践性、探索性、层次性、指导性、及时性、鼓励性、发展性，将承载学生数学思维发展的作业设计落实，以帮助学生数学思想的形成.

例如，解直角三角形中有这样一道题：在某一热气球上看向某大楼顶部时的仰角是30°，看向其底部的俯角是60°，热气球跟大楼之间的水平距离有120 m，该幢大楼的高度是多少米（结果保留小数点后一位）？笔者在这一解直角三角形的实际问题解决之后又选择了一道中考试题供学生练习：我校数学沙龙社团本周的活动主题为测量旗杆的高度，表1是该社团的部分研究记录，你能根据表中信息求得旗杆AG的高度吗（取1.7，结果保留两位有效数字）？以课题报告形式呈现的作业给学生耳目一新的感觉，学生在这一具有实践性、探索性以及趣味性的作业中也获得了不同的收获与发展.

笔者也因此对问题背景进行了新的审视并设计出了以下作业：①自备工具并自主设计测量旗杆高度的方案，测量时不能放倒或攀爬旗杆；②请在方案设计结束后运用直角三角形知识对方案的可行性进行解释和验证；③将自己设计的方案转化成数学问题并供同伴思考和解决；④评价同伴的解决方案. 一部分学生虽然不能完整而准确地完成这一“另类”的作业，但问题①的解决中却呈现出了勾股定理、全等三角形、相似三角形、解直角三角形等多种方案，出人意料的诸多答案也说明不同认知层次的学生都在问题①的探讨中获得了发展. 问题②和③也令大部分学生体验到了数学转化的基本思想. 可喜的是问题④的完成情况最好，学生在自己当老师的情景下进行了作业的批改、评价甚至建议.

也许很多教师对于笔者设计的作业方案、转化思想的体现会感觉过于复杂，也许有的教师还会认为创新评价是多此一举的，甚至有的还会认为笔者的这一设计是增加学生负担的行为. 但实际上，这些想法都是忽视数学真谛而形成的，研究空间形式与数量关系的数学学科一点都不能缺失探究与思考的“过程”，促进学生思考与探索的过程教学对于增加学生课业负担一说是完全没有根据的.

数学教师在实际教学中要将“减负”与“增效”这“两难”做到“双赢”并不是不可能，教师必须弄懂“减负”与“增效”之间的辩证关系，在知识呈现、情境创设、解题教学、作业设计等环节中进行贴合学生实际的考量与权衡，使得自己的教学能够做到“加减得法”并因此将“减负增效”真正落到实处.