对数学问题1637的探究

李凤清，张子卫

（四川职业技术学院应用数学与经济系，四川遂宁629000）

1 两个引理

为行文方便，先给出两个引理.

引理1 n倍角的余弦公式（文[2]中第（9）式）设是不小于2的正整数，则

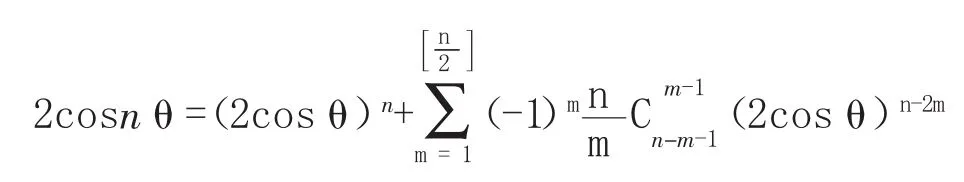
当1≤k≤n时，恒有a0Sk+a1Sk-1+…+ak-1S1+kak=0；

当k＞n时，恒有a0Sk+a1Sk-1+…+an-1Sk-n+1+akSk-n=0.

2 数学问题1637的两个简解

数学问题1637 P是正三角形A1A2A3的内接圆O上的任一点，P至A1A2，A2A3，A3A1的距离分别为d1,d2,d3，问当P点位置变动时，++是否为定值.++是否为定值？说明理由.

原文解答计算量较大，下面先给出两个简解.

解1不妨设圆O的半径为1,设线段A1A3的中点为F，记∠FOP=θ,根据原文解答过程知-θ）.由余弦的三倍角公式，可知当k=0,1,2时，均有-θ）=cos3θ，即d1,d2,d3是一元三次方程4（1-x）3-3（1-x）=cos3θ的三个根，将这个方程化简为

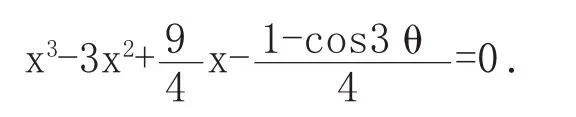
根据一元三次方程根与系数的关系我们可以得到：

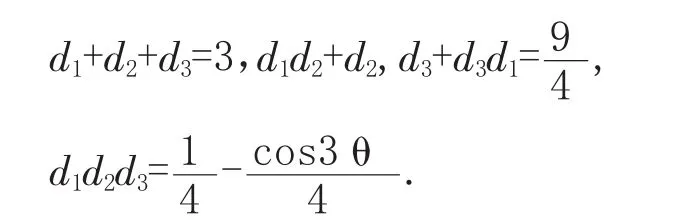
运用牛顿公式，我们即可得到：

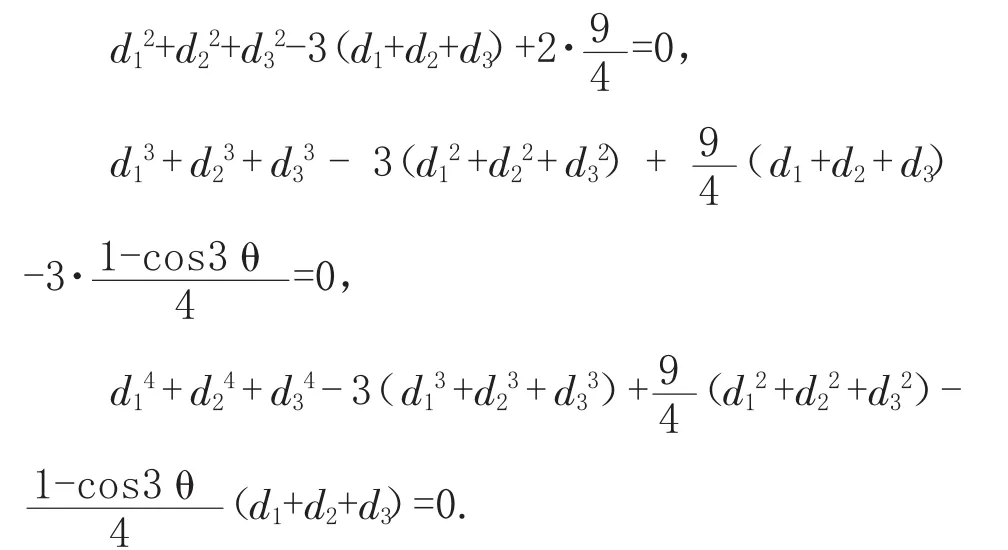
即可得：

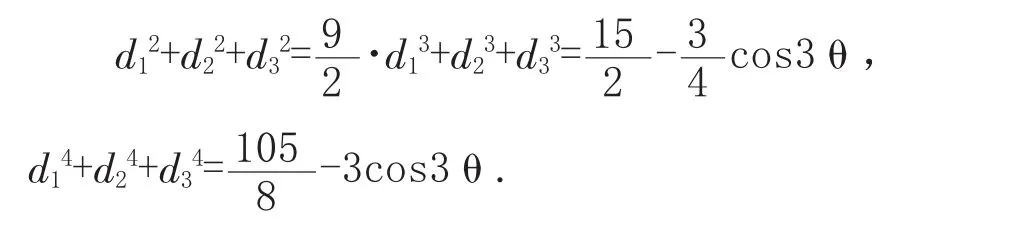
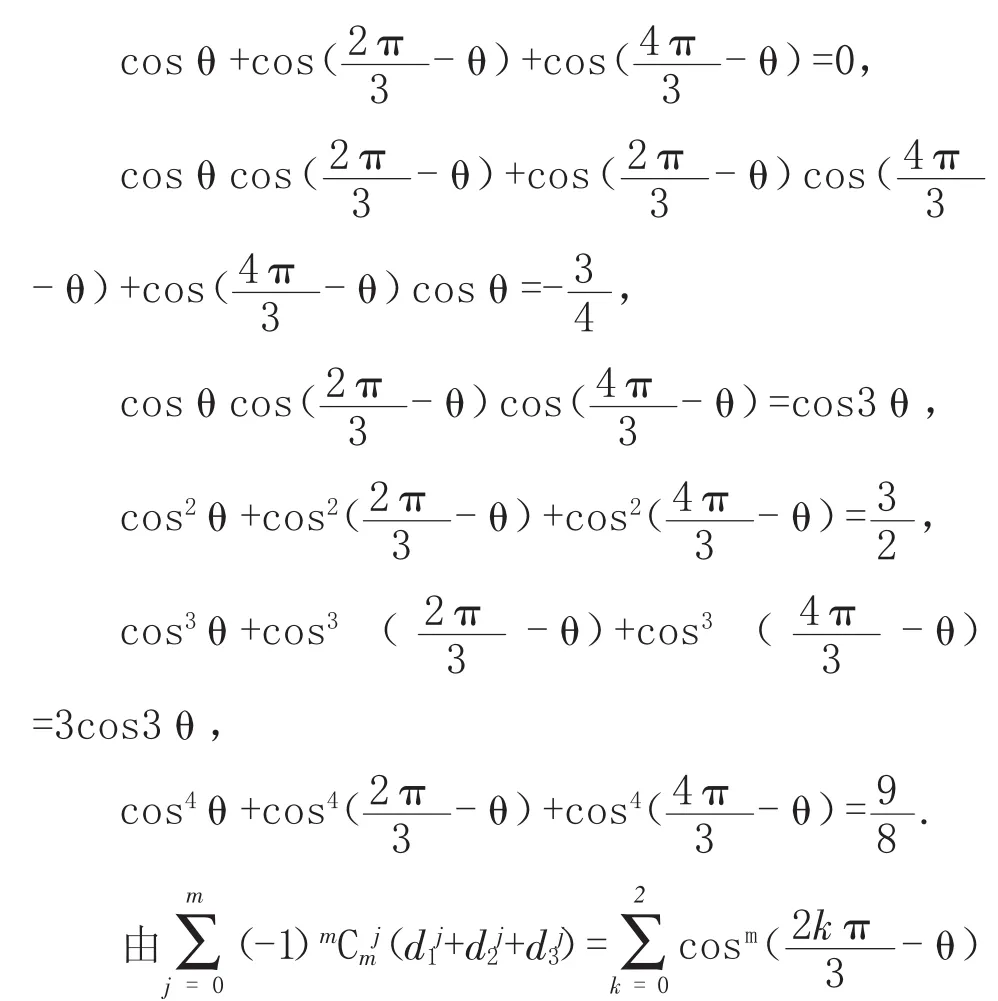
3 一个三角恒等式

由上面解法2可以得到一组三角恒等式.

定理s，n是正整数且n≥3，则

证明根据引理1，当k=0,1,2,…，n-1时，由多倍角的余弦公式可知2cosnθ=2cosn（

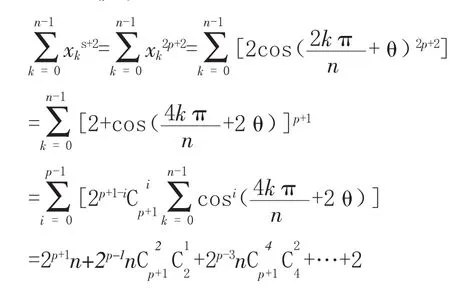
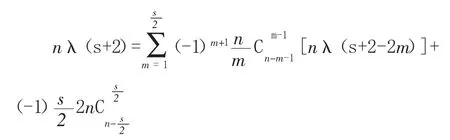
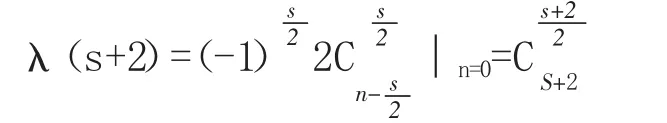
运用上面定理，我们可把上面问题推广到正多边形，得到下面结论.

命题正n边形A1A2…A（nA1，A2，…，An按逆时针旋转排列）的中心为O且内切圆半径为R,圆O在正n边形A1A2…An的内部且半径为r，P是圆O上任一点，P至A1A2，A2A3，…An-1An，AnA1的距离分别为d1，d2，…，dn，记，则当m=1,2,…,n-1时，S（m）为定值；当m=n，n+1时，S（m）不为定值.

证明类同上面的证明2，此处略去，留给读者.

[1] 王君丽.n倍角的余弦公式[J].昭通师范专科学校学报，2006,（10）.