线性变换的零化多项式与线性空间的直和分解

邹宗兰

(四川职业技术学院应用数学与经济系，四川遂宁629000）

1 预备知识

设V是数域P上的一个n维线性空间，σ是V的一个线性变换，f（x）是数域P上的一个多项式，如果f（σ）=0，则称f（x）零化σ．我们用σ（V）或σV表示σ的值域，σ-1（0）表示σ的核．根据哈密顿-凯莱定理，线性变换σ的特征多项式是σ的零化多项式．参考文献[1]第309页的定理12证明了

如果线性变换σ的特征多项式f（λ）可分解为一次多项式的乘积

那么V可分解为不变子空间的直和

其中Vi={ξ│(σ-λi)riξ=0,ξ∈V},i=1,2,…，s．（ε表示恒等变换）

本文将把上述结果推广到线性变换σ的任意零化多项式的情形，即设f（x）是线性变换σ的任意一个零化多项式，我们利用f（x）的标准分解式把线性空间V分解成的σ一些不变子空间的直和．

2 利用线性变换的零化多项式对线性空间作直和分解

定理1设σ是数域P上的n维线性空间V的一个线性变换，数域P上的多项式

使得f（σ）=0,f1（x）,f2（x）,…,fs（x）两两互素，再设

那么1）fi（σ）-1（0）=gi（σ）-1V,gi（σ）-1（0）=fi（σ）V,i=1,2,…，s；

2）V可分解为σ的不变子空间的直和

证明：1）由gi（x）的定义知fi（x）gi（x）=f（x），于是

另一方面，因为f1（x）,f2（x）,…,fs（x）两两互素，所以fi（x）与gi（x）=f1（x）…fi-1（x）fi+1（x）…fs（x）互素，从而存在ui（x）,vi（x）∈P[x]使得

这样对于Vi的任意一个向量α有

因此α∈gi（σ）V这就证明了

由（1），（3）得gi（σ）V=fi（σ）-1（0）=Vi，i=1,2,…，s.

2）由于σ与fi（σ），gi（x）可交换，所以fi（σ）的核fi（σ）-1（0）和gi（σ）的gi（σ）像gi（σ）V都是σ的不变子空间．

由f1（x）,f2（x）,…,fs（x）两两互素不难知道g1（x）,g2（x）,…,gs（x）是互素的，因此存在多项式hi（x）∈P[x],i=1,2,…，s使得

于是

对于V的任意一个向量ξ，由（4）式得

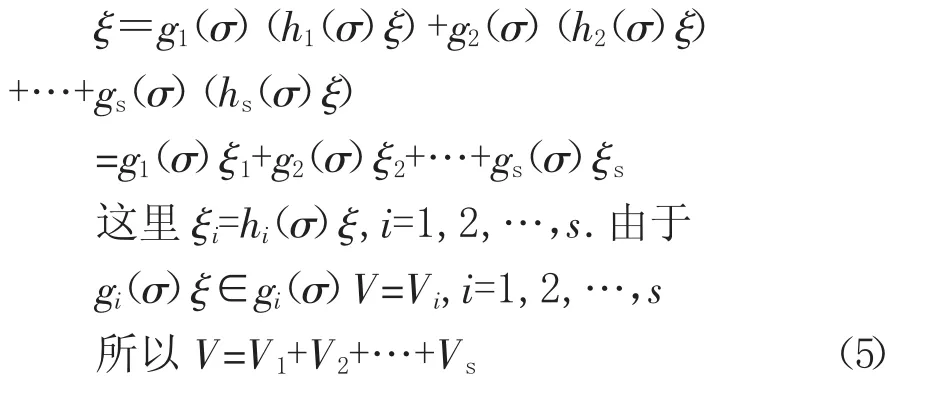
下证（5）是直和．设γi∈Vi,i=1,2,…，s,使得

因为gi（σ）=f1（σ）…fi-1（σ）fi+1（σ）…fs（σ），所以当j≠i时，Vj=fj（σ）-1（0）的元γj在gi（σ）之下的象为零，即

于是用gi（σ）作用于（6）的两边得

根据（2）和（7）式得

这就证明了

由（5）和（8）式得

根据这个定理，我们立刻知道参考文献[1]第309页的定理12给出的结果是定理1的一个推论.对于线性变换σ的最小多项式m（x）∈P[x]同样可得到下面的结论：

定理2设σ是数域P上的n维线性空间V的一个线性变换，为σ的最小多项式，它在数域P上的标准分解式为

证明：取f（x）=m（x），令f1（x）=Piki（x），i=1,2,…，s，则f1（x），f2（x），fs（x）和f（x）适合定理1的条件．

定理3设σ是数域P上的n维线性空间V的一个线性变换，m（x）为σ的最小多项式，那么存在V的一组基，使得σ在这组基下的矩阵是对角形矩阵当且仅当

证明：如果σ在基α1，α2，…，αn下的矩阵是对角形矩阵A．不妨设

其中EKi表示ki级单位矩阵，λ1，λ2，…，λs互不相等，k1+k2+，…，ks=n，那么σ的最小多项式m（x）=（x-c1）（x-c2）…（x-cs），这里ci=cj,i=1,2,…，s．

反之，如果σ的最小多项式m（x）可分解为不相等的一次因式的乘积

设αi1，αi2，…，αiri为Vi的一组基，i=1,2,…，s,r1+r2+,…，rs=n，那么α11，α22，…，αir1，…αs1，αs2，…αsrs是V的基，而αi1，αi2，…，αiri是σ的属于特征值ci的特征向量，故σ在这组基下的矩阵是

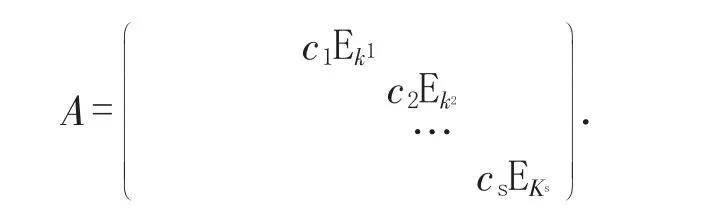
3 结语

由前面的讨论可知，定理1给出的结果具有一般性，而将f（x）取为线性变换σ的特征多项式或最小多项式时，都是定理1的特殊情形，可作为定理1的推论处理．因此在讲授这部分教材时我们建议将参考文献[1]第309页的定理12改为本文的定理1．

我们知道，数域上的一个线性空间的全体线性变换的集合做成数域上一元多项式环的上的模．在这个模中,一个线性变换零化多项式的集合是环的一个理想，称为这个线性变换的零化子．在模论里，模元素的零化子可用来刻画模的结构．因此，在高等代数里讨论用一个线性变换的零化多项式来构作线性空间的直和分解问题，对于学生将来学习模论是有益的．

[1] 万哲先.代数导引[M].北京：科学出版社，2004：231-239．

[2] 北京大学数学系几何与代数教研室.高等代数［M］.北京：高等教育出版社，2003：242-272．