借助几何直观 培养学生数感

杨熠

摘要：“几何直观”和“数感”虽是两个不同领域的内容，但“幾何直观”具有直观的形象，可以解决抽象性的“数感”问题。教师可从“理解数的意义、把握数的大小、辨析运算定律、明晰数量关系”等四个方面利用“几何直观”培养学生数感。通过降低学生的思维难度，减少数学的抽象性，给学生提供一条更为明晰的思维路径。

关键词：小学数学；几何直观；数感；培养

中图分类号：G623.5 文献标识码：A 文章编号：1009-010X（2017）25-0027-04

“数感”是《义务教育数学课程标准（2011年版）》的十大核心关键词之一，主要是指关于数与数量、数量关系、运算结果估计等方面的感悟。众多学者一致认为“数感”是一种直观的感悟。史宁中教授认为：“数感是对数的感悟，它表现为对量与数的一种直观能力。”詹国良认为：“狭义的数感就是数字感，即人脑对于数字或数字运算定律的直觉；广义的数感就是数学感，即人脑对于数学对象的直觉。”叶蓓蓓认为：“数感是一种关于数字的直觉”。

数是对数量的抽象。数的意义、大小、运算、数量关系等都相对抽象，要培养直观的“数感”，就需要通过直观的手段。史宁中教授指出：“在教学中，要为学生提供丰富的情景，引导学生通过观察，感悟量的多少，促进学生数感的发展。”

“几何直观”和“数感”虽是两个不同领域的内容，但如果能利用图形把抽象的数直观地表示出来，搭建通往“数感”的桥梁，就能化抽象为形象，加深学生对数的理解和感悟。更重要的是，几何图形的直观性能帮助学生在脑中建立起相关的模型，促使学生在以后遇到类似问题时能自觉地利用图形进行思考，达到“学生自觉地感悟（或意识）”。本文将从“理解数的意义”“把握数的大小”“辨析运算定律”“明晰数量关系”等四个方面人手，阐述如何借助几何直观，培养学生数感。

一、借助直观图形，理解数的意义

理解数的意义是“数感”的主要表现，也是数学教学的重要任务。《义务教育数学课程标准》在不同学段都提出了“理解数的意义”的目标，如第一学段提出：“经历从日常生活中抽象出数的过程，理解万以内数的意义”；第二学段提出：“理解分数、小数、百分数的意义，了解负数的意义”等。数的意义本身是抽象的，学习时需要给学生提供具体的可供感知的素材。但随着数的范围的扩大，数与具体事物的对应会变得困难，影响学生对数的意义理解。

生活中的“数”总是和“量”紧密相连，不同的量会带给学生不同的感受。如“1000”，1000粒大米和1000颗黄豆对学生造成的感觉是不一样的。几何图形，正可以摆脱“量”的羁绊，让学生把注意力更多的集中到“数”的层面。

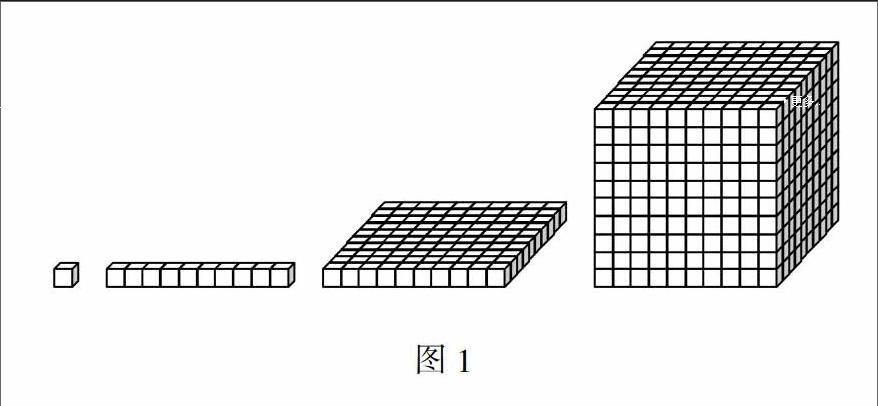
教学中可以借助立方体来说明“一千”，借助直观图形，让学生理解“千”作为计数单位和“个（一）、十、百”之间的关系，感受计数单位之间“满十进一”的十进制计数法；并通过观察1000与500、200、100之间的联系，最小四位数和最大三位数之间的联系等，帮助学生从多个角度理解“1000"，培养学生的数感。

（一）理解千与“百、十、个（一）”的关系

1.结合图形（图1）数数：一个一个数，10个一是十；十个十个数，10个十是一百；一百一百数，10个一百是一千。

2.师：你有什么发现？

生：都是十个十个的。

生：10个一是十，10个十是一百，10个一百是一千。

生：都是10倍的。

生：……

（二）多角度理解“1000”

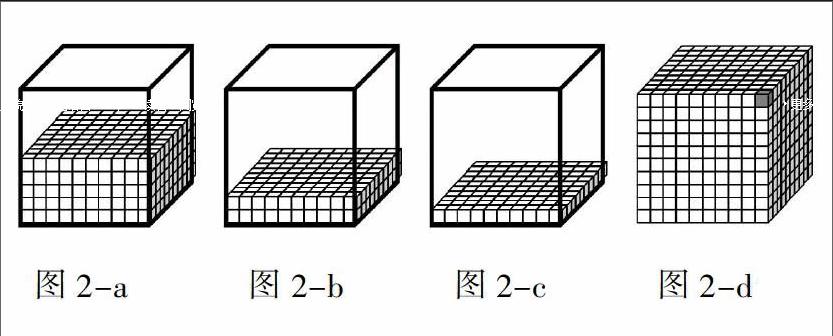
1.从1000里面去掉一层，还剩多少？再去掉100呢？……一直到去掉5个一百，还剩几百？一千里面有几个五百？……1000里面有几个2007有几个1007（图2-a、2-b、2-c）

2.1000去掉1后还有多少？（图2-d）（生：999）沟通“最小四位数和最大三位数”。请学生指出哪里是900，哪里是90，哪里是9。如果把这个“1”放回去，第一排9个加1个就满十；这个十加上90就是100，100加上900就是一千。让学生体会“满十进一”。

当数的范围扩大后，借助直观图形，对数进行分解与组合，用不同方法思考数、表示数，能加深学生对数的意义的理解。

二、结合直观演示，把握数的大小

史宁中教授指出：数的关系的本质是数的大小。在具体的情境中把握数的相对大小关系，不仅是理解数概念的需要，同时也会加深学生对数的实际意义的理解。结合直观演示，动态展示“数”的形成及大小关系，能促进学生把握数的大小。

如“分数”，它既表示部分与整体之间的关系，又表示一个数。在教学“分数的意义”时，可以借助长方形和线段辅助教学，把“数”在“形”的一一对应中找出来，理解数的意义和大小。

（一）把一个长方形平均分成2份，每份就是这个长方形的1/2.

（二）把一个长方形平均分成3份，每份就是这个长方形的1/3.

……

这样不但帮助学生理解了分数的意义，还能让学生直观地感受到分数的大小。接着再深入一步，把分数在数轴上表示出来，形成完整的数的序列。

（三）如下图（图3-a、图3-b、图3-c、图3-d）一个长方形就代表1，2个长方形就代表2，三个长方形就代表3.

1.

2.加上数字：

3.让学生在图中找到1/2和1/3。

（四）把长方形逐渐压缩，成为一条线，形成数轴，构建数的体系。

（五）让学生找一找1/4在哪里，再思考，1/10可能在哪里？

数字之间的关联与顺序是数感的重要体现。通过“数”与线段上点的对应，结合直观演示，完整的数序列就直观地呈现在学生的面前了，扫清了对数大小理解的障碍，还为后续的学习及大小比较等做了铺垫。endprint

三、依托图形表征，辨析运算定律

运算定律是在抽象的数的基础上对数之间关系的再抽象，运算律的运用是数感形成的标志。灵活分辨和运用运算定律，对学生来说是一件困难的事。究其原因，在于没有一种形象直观的表征方式能让学生体会不同运算定律之间的区别。对运算定律进行图形表征，让学生在应用时能自觉地在脑中产生相对应的图形模型，有助于加强学生对运算定律意义的理解，正确辨析。

如乘法结合律与乘法分配律，可以这样教学：

（一）把4个长25、宽7的长方形排成一排，组成的大长方形的面积是多少？请先画图，再列式说明。（得到两种图形：图4-a和图4-b）

得到4×25×7或25×（4×7）

比较：哪种方法计算时更简便？

（二）两个分别是长25宽4，长7宽4的长方形组成一个大长方形，大长方形的面积是多少？请画出示意图（图5），并列式计算，得到25×4+7×4或（25+7）×4.

（三）比较两道题目和图形，有什么发现？让学生理解乘法结合律相当于求若干个相同长方形的总面积，乘法分配率相当于求由两个一边相等的小长方形组成的大长方形的面积。

（四）试着用图形语言去解释算式：63×25+37×25，63×37×25.比較这两个算式的区别。

通过联系、沟通图形表征与算式表征，帮助学生深入理解运算定律，产生自觉利用图形进行辨析的意识，大大减少了两者混淆的情况。

四、建立直观模型。明晰数量关系

数学的“解决问题”是对生活现象的高度抽象，抽象的数量关系导致学生在理解上的困难。

现行小学数学教材弱化了数量关系的教学，要求学生在具体的问题情境中去探索、去发现数量之间的关系。这固然可以起到避免思维固化与模式化的作用，但一定程度上也提高了学习难度。教学中应建立直观模型，明确地表示出数量之间的关系，降低思维难度，获得解决问题的方法和能力。

线段图是“几何直观”应用的典范。除了线段图，教学中还可以根据题目和学生的思维发展情况，适度借助其它几何图形，更好地直观展示出题目数量之间的关系。

如“一桶水连桶共重16千克，倒掉半桶水后连桶重9千克，水和桶分别重多少千克？”。这样的题目变换数字后，在二年级到六年级都会出现。对于低年级学生来说，难度较大，即便是加上线段图的辅助都还比较抽象。我在教学中给学生提供了如下的图形（图6）：

通过图形演变，学生会发现16-9在解决这个问题中的作用。再让学生列式，结合图理解每一步算式的意思，巩固解题方法。学生一般还能想到其它的解法：9-16÷2=1，1×2=2，16-2=14.或9×2-16=2，16-2=14.让学生根据思路画出图形，把解题思路形象化，进行巩固。

直观图形的使用不仅能帮助学生理解题意，解决问题，更是帮助学生建立起了解决问题的直观模型。到了高年级，遇到类似“一桶水连桶共重17.75千克，把水倒出1/2后，重12.25千克，空桶重多少千克？”的题目，学生也能通过画图轻松解答了。

数学的直观，是开启儿童学习数学大门的钥匙。根据教学内容，借助几何直观，能降低学生的思维难度，减少数学的抽象性，给学生的思维发展提供明晰的路径。教师应深入理解几何直观与数感的本质，巧妙借助几何图形，把抽象的数的意义、大小、运算、数量关系等直观地表示出来，帮助学生建立自觉理解数和运用数的态度与意识，培养学生数感。

【责任编辑 王悦】endprint