一道习题的解法、推广及拓展

福建省福安市第二中学 林如翰

教学中发挥例习题的功能，有利于学生掌握知识、提高技能，形成能力。因此，教师在讲评例习题中，注重并挖掘例习题的本质，探究例习题的价值，对培养与发展学生的数学思维能力具有重要意义。本文通过一个习题的解法、推广及拓展，并结合自己的教学实践谈谈感悟与思考。

一、习题及解法

题目：如右图，已知抛物线y2=4x的焦点为F，过焦点F的直线l交抛物线于A、B两点，O为坐标原点，若△AOB的面积为求弦长

解法1：依题可知l的斜率存在，设直线l的方程为y=k(x-1)且k≠0，代入抛物线方程y2=4x得[k(x-1)]2=4x，即k2x2-2(k2+2)x+k2=0，则Δ＞0且原点O到直线l的距离为所以△AOB的面积

解法2：设直线l的方程为x-1=my且m≠0，将x=my+1代入抛物线方程y2=4x得y2-4my-4=0，则Δ＞0且y1+y2=4m，y1y2=-4，所以则

解法4：以焦点F为极点，Fx为极轴建立极坐标系，则抛物线y2=4x的极坐标方程为所以令点A的极坐标为(ρ1，θ),则点B的极坐标为(ρ1,θ+π)，所以原点到直线l的距离d=1×sinθ，且=6。

二、推广与拓展

1.最值问题

若解析几何中的相关长度、面积、斜率、离心率等几何量是某变量的函数，则都可以转化为求目标函数的最值问题，这是函数思想方法在解析几何中的应用。

解：不妨设直线l1的倾斜角为θ且则直线l2的倾斜角为由以上可得弦长当sin2θ取得最大值为1时，即取得最小值，为8p。

2.轨迹问题

圆锥曲线中有许多丰富的、有趣的轨迹问题，如某动点轨迹、中点轨迹、相关点轨迹、重心轨迹、垂心轨迹等问题，都是十分有趣、有益的探究学习活动。

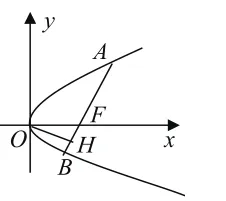
例2 已知抛物线点F的直线l交抛物线于A、B两点，O为坐标原点，过点O作弦AB的垂线，垂足为H，求H的轨迹方程。

3.对称问题

圆锥曲线中的对称问题包括点关于点的对称、曲线关于点的对称、曲线关于直线的对称等，抓住中点坐标与斜率关系是处理这类问题的关键。

解：（1）当直线l的斜率不存在时，显然抛物线上不存在两点C、D关于直线AB对称；

三、启示与展望

通过一道习题的求解及拓展、探究并解决解析几何中常见问题，从中感受抛物线焦点弦所蕴含的丰富数学内容。在数学教学中实施探究性学习，提升学生探究能力和学会数学地思考，有利于培养科学精神、数学思维品质与能力，从中体会到弗赖登塔尔的“再创造”原理。数学教学方法的核心是学生的“再创造”，应引导学生经历数学“再创造”、交流数学和应用数学，同时也启发我在今后的教学中应充分挖掘习题的潜在功能与价值，为追寻数学教学之道而努力。

[1]裴金楼.抛物线焦点弦的几条性质[J].数理天地（高中版），2007（10）：4-5.