例谈初中数学“题·问”的顺敞性设计与实践

江苏省苏州工业园区星洋学校 杨雪华

一、顺敞性——顺在“水到渠成”

《数学课程标准》指出：数学课程内容要符合学生的认知规律，要贴近学生的实际，有利于学生体验与理解、思考与探索；教师教学应该以学生的认知发展水平和已有的经验为基础，注重启发式和因材施教，要引导学生独立思考、主动探索、合作交流，使学生理解和掌握基本的数学知识与技能、数学思想和方法，获得基本的数学活动经验。具体实践中，在课堂上，学生掌握数学知识不能依赖死记硬背，而应以理解为基础，并在知识的应用中不断巩固和深化新知。

笔者曾在一次公开课上执教了一个直线公理：经过两点有且只有一条直线。当时就有学生提出：他过两点画出了两条直线。这是一个让笔者有点意外的问题，公开课后，很多数学老师都津津乐道于此问题（如图）。

课堂实录：“过两点我画出了两条直线。”

生1：老师，“经过两点有一条直线，并且只有一条直线”这句话是错的。

图2

笔者：为什么？

生1：老师你看，过两点我画出了两条直线。如图1。

笔者：同学们，他的发现好像有道理，你们能不能再深入思考？

生2：老师，好像经过点A、B还可以再画一条。（如图2）

笔者：画得很好，按这样的画法，一共可以画几条呢？

生：争论，画出的条数越来越多。

笔者：仔细想一想，为什么能够画出这么多条直线？

生3：点越大，能够画出的直线的条数就越多。

笔者：那么点到底可以画多大呢？

生4：老师，点是没有大小的。

笔者：总结得很好，那刚才为什么过两点可以画很多条直线呢？生5：点画“大”了。

生6：点“大”了就变成了平面，在平面上画直线就有很多条了。笔者：善于仔细观察和思考，就能剖析疑惑、解决问题。

笔者的课堂生成是紧紧围绕该学生的观点，引导他步步深入、作图验证，得出了“过两点可以画出无数条直线”的命题，再进一步让学生研究其原因。得出的结论是“点画大了”，再追问“点有没有大小呢？”至此，这个课堂尴尬“顺思”迎刃而解，可以看出本节课的释疑解惑“顺敞性”设计是成功的。

学生的疑惑和不解往往是理解不畅导致的，很多时候是一种误解，只要耐心地顺着他的想法“将错就错”、“用其之矛攻其之盾”，就能够很好地让学生理解和掌握数学知识。

二、顺敞性——敞在“透明思维”

教学实践中，我们的课堂讲解、启发引导的出发点和指向性都是为学生理解知识、掌握技能服务的。但实事求是地讲，我们的课堂可能还或多或少地存在着教师的“教”与学生的“学”脱节的情况，而学生的想法“不敞”是其中的一个重要原因，这也导致了少部分数学课的教学效率稍显低下。为此，打开学生的心扉，了解学生的思维习惯，遵循学生的认知规律，注重数学知识与学生生活实际的联系、与学科知识的联系，这就成了敞开思维、提高效率的前提条件。一次教研活动中，一位教师讲解了如下问题：

已知：如图3，线段BE和CF是△ABC的中线，它们相交于点G，

求证：FG∶GC=EG∶BG。

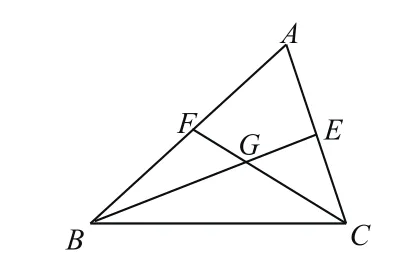
图3

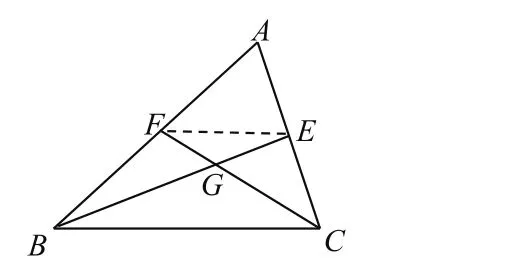
图4

课堂上，执教老师可能会忽略学生的思路，分析时直接提出了连接EF（如图4），让学生证明△EFG∽△BCG，得出求证的结论。这样的教学可能错过了一个很重要的数学资源，教学实践中，如果敞开学生的思维过程，学生就可能会出现证明△BGF和△CGE相似。事实上，这个结论是不成立的。笔者认为在教学中不要急于纠正错误结论，而要让学生讨论，自主判断这两个三角形是否相似？进而得出“中点出现时”的常规处理方法，让学生合作归纳出中点出现的试题经常使用的解题通法。

所以，笔者觉得教师在备课时要认真揣摩学生的心理，估计学生可能发生的各种情况，先将不正确的思路自主排除，再将学生引入正途，这时的学生不需启发，自然而然地就会利用“E、F分别为AC、AB的中点”的条件，连接EF解决此问题。

三、“题·问”是顺敞性设计实践的抓手

课堂教学是一个“研无定法”的深奥话题，笔者在一线教学实践中主张的“顺敞性”，其实是数学课堂教与学链接的最核心要素，而其抓手则是“试题”与“问题”，一线教学中也有较多老师的课堂教学就“提问”谈“提问”，不能与“顺敞”和“问题”本身有效联系起来。本文中所谓的“题问”实际上是对题的一种理解和感悟，能够找到独特的视角、精准剖析、突破疑点。“题”是“问”的基础和源泉，“问”是“题”的内涵和升华，“题问”、“顺敞”是相辅相成的共同体，而“顺敞性”则是“题、问”的纽带，是解决数学教学中疑难问题的有效手段，它是初中学生学习数学、思维发展、知识生成、能力提升的有效途径。