数学品格形成“四部曲”

福建省泉州市丰泽区实验小学 伍媚燕

品格是指一个人的人品和做事风格，而在数学教学中，“数学品格”是指在数学学习当中所表现出来的积极的思维态度、科学严谨的思维方式、强烈的思维内驱力、密集的脑力思维容量等方面的品格，它是数学教学中的重要部分。因此，我们在教学中要以数学品格为核心去培养学生的数学素养。

一、问题解决，奠定数学品格之基础

在数学教学中，我们的主要目的是培养学生运用所学的知识去提出问题、发现问题、分析问题以及解决问题的能力。问题解决能力是指学生从发现问题到解决问题的全过程，在这个过程中，学生能够积淀自己的数学活动经验，从而能够促进数学素养的养成。正如弗赖登塔尔所认为的，“数学化”包括横向数学化和纵向数学化，横向数学化是考验学生的数学猜想力、判断力等等，而纵向数学化是指学生的数学逻辑力和推断力，而这正是问题解决的关键，奠定学生数学品格的基础。

例如，在学习《分数》时，教师在教学的过程中先给出一道题目让学生进行思考，学生在这个过程中可以把数学化的思想运用到解决题目的过程中，教师在教学的过程中也可以运用对话的形式对学生数学品格的形成起到一定的效果。

师：有一根绳子，要平均分成5份，把第一段绳子剪断需要2分钟，那么我们把绳子平均分成5份，同学们猜猜要多少时间？

生1：剪断第一份绳子需要2分钟，那么把绳子弄成5段，就需要10分钟。

生2：不对，断第一份绳子需要2分钟，那么把绳子剪成5段，只需要剪4次，只需要8分钟。

生3：我赞成生2的说法。

……

学生在这个对题目的解答过程中，就运用到了数学化的思想，如让学生猜猜锯掉钢管共需要多少时间，就是考验学生的猜想力，而学生在解题的过程中列出的算式就是对纵向数学化的运用，学生在这个过程中运用数学化的思想解决了问题，并且奠定了数学品格的基础。

二、数学思维，形成数学品格之关键

数学是一门抽象化的学科，因此在数学教学中，教师要引导学生运用思维的方法去学习具体的知识内容。教师应基于思维教，围绕思维学，让学生去发散自己的思维，从而让学生养成良好的数学品格，这是养成数学品格的关键。

例如：一根竹竿长9米，一只蚂蚁从下往上爬，蚂蚁白天向上爬3米，晚上向下掉2米，那么蚂蚁要用多少天才能爬到顶端？

师：按照正常的逻辑来推算，蚂蚁爬上竹竿的时间是需要9天，你们觉得这样对吗？

生1：我们从蚂蚁实际的爬行情况分析，蚂蚁在最后一天爬行的时候，往上爬3米后就不会再掉下来了，所以只需要8天的时间就可以了。

生2：题目中问的是蚂蚁需要多少天，而不是具体的哪一天。蚂蚁在前8天就已经爬上了4米，而在第8天的白天就达到顶端了，按每天24小时来计算，所以蚂蚁只用了8天半的时间就爬上了顶端。

生3：答案为8天，蚂蚁在第7天的白天刚好达到顶端就又开始往下掉，不能算成功登顶了，而第8天要爬3米，所以无论如何都爬上顶端了。

……

这一道题目考验了学生的理解能力，学生凭借理性的思考去领悟知识的本质，在这个过程中，学生学会用不同的角度去考虑问题，同时也是对他们思维的发散和拓展，让他们有自己的思想，实现他们的主体意识，学会自主思考、自主判断和分析，正是对他们数学思维能力的培养，也是对他们数学品格养成的关键之处。

三、数学思想，赋予数学品格以质感

数学思想是教师教学过程和学生学习过程中的精神实体，在数学思想中贯穿着转化思想、假设思想、实验思想等等，数学思想因其内涵性和紧凑型而赋予数学品格以质感。著名日本学者米山国说：“作为知识的数学出校门不到两年就忘了，唯有深深铭记在头脑中的数学精神、数学思想、研究方法和着眼点等，随时随地地发生作用，使人终身受益。”因此，在小学数学教学中，教师要有意识地渗透数学思想，让学生明白数学思想的重要性。

例如：甲、乙两个城市相距357千米，有两辆车（快车和慢车）分别从两个城市相向而行，快车每小时行驶79千米，3小时后两车相遇，问慢车平均每小时比快车少行多少千米？

师：请同学们用不同的方法进行解答。

生1：我列出的算式是[357-（79×3）] ÷3=40（千米），快车每小时行驶79千米，所以79-40=39（千米）就是答案。

师：这是运用数学思想中的类比思想，同学们还有其他的方法吗？

生2：我还有其他的方法，我同样也是用类比的思想，79-（357÷3-79）=39（千米）。

师：其他同学还有吗？

生3：我有，假设慢车平均每小时行驶x千米，则有79×3+3x=357，解得x=40，79-40=39（千米）。

师：好，这个同学运用了假设的数学思想，同学们还有其他解法吗？

生4：假设慢车平均每小时比快车少行x千米，则有（79-x）×3=357-79×3。

师：这也是对假设思想的运用，同时也是运用了转化思想。

……

学生在数学思想的指导下，对一道题目进行了一题多解。在这个过程中，学生的数学思维得到了培养，同时这种思想也深深地印入了脑海中，并让数学思想成为学生主体能动的认知，让他们在相互探究中学习，去探究数学思想给他们带来的乐趣，同时也培养了学生的数学品格。

四、文化精神，闪烁数学品格之光辉

数学文化也是一种文化，数学教学必须以一定的数学品格来濡染学生的身心，让学生练就一定的数学品格和眼光。数学文化不仅包括数学的思想方法，更包括数学的情感，对数学学习的态度以及学习数学后对数学形成的价值观等等。数学文化来自学生对数学内在美的追求、对数学精神文化的追求。例如，在学习《找质数》这一课时，教师在这个过程中就让学生体会到了数学文化的源远流长，感受数学文化的精神及魅力。

师：早在两千多年前，希腊数学家就想出了一个有趣的方法来寻找质数，那我们一起来看看他的方法。（教师在黑板上出示1～100的表格及方法）

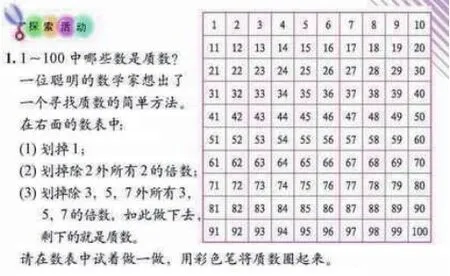
生1：这个方法有些看不懂，老师能给我们讲讲吗？

师：好，我们来看看，我们按照他的方法看能不能找出质数。先划掉1，然后划掉除2以外的2的

倍数，再划掉除3、5、7之外的它们的倍数，那我们看看通过这个方法能不能找出质数。

生2：（通过观察和动手）发现这样做了之后就得到了质数，并且不会有错。

生3：我们划去2的倍数、3的倍数、5的倍数、7的倍数……（除了这些数本身外）其余的数都是合数，那么自然而然地，剩下的数就是质数了。

师：是的，这个同学说得很对，他的这个方法是筛选法，把合数筛去，剩下的就是质数了。

在这个过程中，教师让学生了解了质数的定义，同时通过对希腊数学家的方法进行验证，从而加深了对质数的认识，增加了课堂的文化底蕴和史实韵味，同时渗透了数学文化，激发了学生的学习热情，使学生在学习过程中感受到数学文化的源远流长和无穷魅力，对其数学品格的养成也有一定的帮助。

爱因斯坦说：“素质是一个人遗忘了在学校所学的知识后所剩下的东西。”那么对于小学数学来说，我们所剩下的就是数学品格了，培养学生的数学思维，渗透学生数学思想，让学生在数学学习中感受数学的文化魅力，才能让学生的数学品格得到完善，真正成为学生的数学核心导向。