例谈核心素养引领下的高中数学教学中例题的选择
江苏省外国语学校 严良惠
数学核心素养反映了数学的本质和教学思想,作为数学教学中一个重要环节的例题教学,无疑是培养学生核心素养的重要途径,学生通过例题的学习,将知识、技能、思想和方法联系在一起,发展了思维能力,逐步学会了分析问题和解决问题的策略和方法。因此,对教师而言,例题的选择十分重要,不仅要考虑培养学生基础知识、基本技能类的基础题,更要考虑发展学生思维的能力题;不仅要考虑选题利于培养单一思维能力,还要考虑学生的思变能力;不仅要分析所授例题的类型、几个例题之间的异同点,还要有利于让学生学会解决问题的方法。只有精选例题,教师才能掌握教学的主导权,才能有效提高课堂教学的效果。
一、例题有利于抽象理论知识的理解
高中数学概念的高度抽象性与学生思维的具体形象性形成了矛盾,造成了学生在理解概念时一种复杂的特殊的心理过程。而例题可帮助学生进行思维的调控、升华、沉淀,进而帮助学生顺利地建构知识。
例1:已知A={x|x<0},B={y|y<-1},求A∩B,A∪B。
通过该例题的设计,学生首先要正确理解集合的有关概念,特别是集合中元素的三要素;对于用描述法给出的集合{x|x∈p},要紧紧抓住竖线前面的代表元素x以及它所具有的性质p;重视、发挥图示法的作用,通过数形结合直观地解决问题。
因此,落实所学知识,让学生在解题过程中体验,促使内化的生成,进而生成解决此类问题的思路,从而展示知识的发生过程,促进知识的迁移,并强化知识的内在联系,加强知识网络的形成,有利于学生将所学知识融会贯通,提高其解题能力,促进数学思维的形成,提高数学素养。
二、例题有利于激发学生的思维能力
新课程标准要求学生自主探索学习,强调培养学生应用数学和创新能力,鼓励教师创造性教学。那么,教学如何从静态转为动态?如何指导学生独立分析、解决问题,并形成有效的学习策略?引导学生进行一题多解和多题一解的训练,将会对这些问题做出一些解答。在高中数学教学中贯彻“一题多解”与“多题一解”的思想,其作用是培养学生的数学思维,在教学中应教学生掌握基本的解题模式和方法,形成必要的解题技能,有利于掌握一定的探索数学问题的能力。
1.一题多解
在高中数学教学中选择一题多思、一题多解、一题多讲的例题,可巩固知识点,训练学生的思维,开拓学生的视野,使学生善于从多角度、多方位去探索同一个问题,不仅可以开阔解证问题的思路,同时提高了应变能力,而且最大限度地挖掘了学生已有知识的潜在能力,使学生克服了思考问题的片面性,避免了顾此失彼而孤立地分析问题,进而潜移默化地提高了审题能力。因此,从多角度去看一道题,强化了思维的连贯性和知识的衔接性,并利用所学知识解决实际问题,激发学生思维。
例3:已知正数x,y满足x+y=1,求的最小值。
方法一:(“1”的妙用)令x+2=a,y+1=b,则a+b=4(a>2,当且仅当时取等号。
方法二:(幂平均不等式)设a=x+2,b=y+1,
方法三:(常数代换)设a=x+2,b=y+1,
当且仅当a=2b时取等号。
通过这一道例题的分析与解答,可锻炼学生的思维能力,同时温故知新,这就是一题多解的好处。题目是做不完的,而学生需通过例题的学习来锻炼自己的思维能力。
2.多题一解
多题一解是用一种数学知识解决不同的数学问题,不仅能更牢固地掌握和运用所学知识,而且通过分析比较,可以寻找解题的最佳途径和方法,能够培养创造性思维能力。
例4:设函数f(x)=mx2-mx-1。(1)若对于一切实数x,有f(x)<0恒成立,求m的取值范围;(2)若对于x∈[1,3],有f(x)<-m+5恒成立,求m的取值范围。变式训练:(1)若不等式x2-2x+5≥a2-3a对任意实数x恒成立,则实数a的取值范围为________。
(2)已知a∈[1,3]时,不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为________。
学生要学会灵活变动,随着题目的变化,解题思维也发生变化。只要学生掌握它的精髓,则可解一题懂一类题,进而提高学习效率,激发学习兴趣、创新意识和探索精神。在数学教学中,让学生学会一题多解与多题一解,更是培养学生创新思维能力的有效途径之一。
三、例题有利于创新能力的培养
《数学课程标准》明确指出:“教材编写应以《标准》为依据,提供的素材要密切联系生活实际,让学生体会到数学在生活中的作用,题材应丰富多样,呈现方式应丰富多彩。”
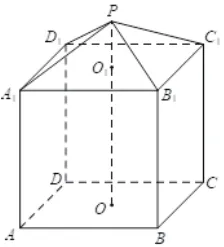
例5:现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥P-A1B1C1D1,下部分的形状是正四棱柱ABCD-A1B1C1D1(如右图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍。(1)若AB=6cm,PQ1=2cm,则仓库的容积是多少?(2)若正四棱锥的侧棱长为6cm,则当PO1为多少时,仓库的容积最大?
联系生活实际进行例题设计,可展现数学的应用价值,让学生体会到生活中有数学,数学就在身边,进而培养了学生学习数学的兴趣及创新能力。例题的开放性能给学生提供更多的思考和探索空间,有利于激发学生的创新精神,促进学生的可持续发展。
四、例题有利于学生养成良好的学习习惯
选择好例题,通过例题的讲解,引导学生养成倾听的习惯以及积极发言、独立思考、质疑问题的能力。

例6:如图,在直三棱柱ABC-A1B1C1中,D、E分别为AB、BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1。求证:(1)直线DE∥平面A1C1F;(2)平面B1DE⊥平面A1C1F。
在课堂上给出例题,学生需思考怎样用数学语言回答,接着要倾听别人的意见,然后反思总结。其中,
倾听别人的意见是一种良好的学习习惯,学生在课堂上能认真倾听老师的讲课和同学们的发言,这样才能积极有效地参与到教学活动中,才能保证课堂活动的有效进行,学生学会了倾听,学习就主动了。总之,培养学生的倾听能力,使学生养成良好的倾听习惯,会提高情商,学会了倾听,也就学会了尊重别人,学会了真诚处事,学会了关心他人,也学会了与他人合作。
高中例题是学生学习知识的桥梁,学习方法的探究,解题方法的示范,能起到贯通知识、归纳方法、熟练技能、培养能力和发展思维等作用,是学生数学学习中培养核心素养的最重要的渠道。因此,高中数学教学中,我们要充分认识到例题环节的重要性,要以新课程理念为指导,切实做到例题设计适度回归生活,关注动手实践,适度倡导合作开放,既关注学生知识技能的发展,又关注学生思维能力、情感态度与价值观的培养,进而为学生的可持续发展能力的培养奠定坚实的基础。

