贮料粒径对筒仓卸料流态及仓壁压力影响的细观机理研究

王世豪，肖昭然，刘克瑾

（河南工业大学 土木建筑学院，河南 郑州 450001）

贮料粒径对筒仓卸料流态及仓壁压力影响的细观机理研究

王世豪，肖昭然，刘克瑾*

（河南工业大学 土木建筑学院，河南 郑州 450001）

从贮料的细观散体颗粒性入手，利用离散单元法对筒仓卸料过程进行模拟。分析卸料过程中粒径变化对流动状态、力链网络以及仓壁侧压力的影响，发现不同粒径对卸料流动状态和仓壁侧压力有较大影响，并探讨了其影响的内在机理。结果显示，粒径越大，卸料压力峰值越大，对筒仓结构的稳定性越不利。卸料过程中仓壁侧压力总体呈现先增大后减小的趋势，并在增大和减小的过程中出现震荡现象。与国内外研究对比，证明了该研究对实际工程具有参考价值。

筒仓；离散单元法；细观机理；流动状态；侧压力

0 引言

目前，国内外多用筒仓储存粮食、煤炭及矿物等散体物料。在筒仓内散体物料的卸料过程中，筒仓侧壁受到的卸料压力峰值比静态压力要大得多，大部分筒仓工程事故都是由这种过大的卸料压力引起的。近几十年来，世界各国专家对此进行过大量的研究，但由于筒仓卸料过程中颗粒的受力及运动太过复杂，所以目前并没有形成统一的计算理论。

由Cundall提出的离散单元法把单个颗粒定义为允许部分重叠的刚性体，颗粒的运动遵循牛顿第二定律。由于颗粒与颗粒可以接触，也可以分离，因此，离散单元法对于解决体系大变形和非线性等问题有着重要作用。目前，离散单元法在采矿、岩土等诸多领域的应用已经相当广泛，该方法也成为研究和分析颗粒材料力学特性的重要工具。

离散单元法已被国内外许多学者证实了其在模拟筒仓卸料中的准确性。Oldal等[1]用离散单元法模拟了不同漏斗角度的筒仓中颗粒在卸料过程中的流动状态和卸料速率，并用试验验证了模拟结果的准确性。Cheng等[2]进行了单出口及双出口筒仓卸料试验，并用离散单元法进行模拟，观察到了在卸料过程中卸料口附近拱的形成。余良群等[3]探讨了筒仓内散体物料密实度与流态的关系，并验证了离散单元法在模拟和分析筒仓内颗粒运动以及筒仓侧壁压力方面具有可行性。陈长冰等[4]用PFC2D研究了筒仓卸料过程中储料的流动状态、颗粒间接触力以及侧壁压力的变化，并将模拟得到侧壁卸料、贮料压力与试验值比较，结果显示其吻合性很好。Wu等[5]用试验和离散元软件研究了筒仓卸料流态及颗粒内部接触力分布，结果显示筒仓几何结构对卸料流态有较大的影响。肖昭然等[6]用PFC建立原型筒仓的实际模型，模拟结果与原型筒仓静态计算结果较为吻合，并研究了筒仓卸料动态压力计超压系数的分布。

尽管前人对筒仓卸料进行了许多研究，但关于贮料粒径对卸料过程影响的研究相对较少[5]。PFC是由美国ITASCA公司研发的离散元数值模拟软件，作者采用PFC2D对筒仓卸料过程进行数值模拟，探讨不同粒径对卸料过程中颗粒流动状态、颗粒速度、颗粒间接触力以及仓壁侧压力的影响，为后续室内模型试验奠定基础。

1 模型建立

为研究卸料过程中粒径变化对流动状态、力链网络以及仓壁侧压力影响，本文共建立4个模型仓，模型仓固定仓体尺寸、颗粒和墙体力学参数。为了明确不同直径的颗粒卸料过程中的流动状态、力链网络以及仓壁侧压力，一组颗粒直径选取小麦直径5 mm，并按等梯度原则选取其他3组颗粒直径为10、15、20 mm，4组颗粒按所占总体积一致的原则分别生成。

模型中颗粒的刚度选取需要与实际相符，刚度过大或者过小都会使模拟结果不准确。如果仓壁的刚度过大，在装料过程中仓内颗粒不易稳定；如果仓壁刚度过小，在模拟中颗粒有可能会穿过墙体。通过模拟计算发现，一般墙体刚度为颗粒刚度的10倍，可较准确地模拟刚性墙体。考虑实际工程中仓壁比较光滑，在模拟中忽略墙壁竖向摩擦力的影响。参考文献[7]确定模型参数如表1所示。

表1 模型参数Table 1 Model parameters

模型筒仓高1 m，直径0.5 m，出口直径0.1 m，位于筒仓底部中心。仓体左右两侧各设置侧压力监测墙10个，测墙高度均为0.1 m，模型筒仓如图1所示。

2 装料过程模拟分析

直径为5、10、15、20 mm的颗粒均采用颗粒自然下落的方法装仓，在筒仓上方连续生成颗粒下落至满仓，通过控制不同直径的颗粒生成数量使筒仓内颗粒所占体积为一定值，满仓时仓内颗粒数量为1 275～20 400不等。并在满仓之后进行静力平衡迭代以使整个系统达到稳定状态，通过观察墙壁侧压力曲线及颗粒不平衡力来判断系统是否稳定。各测墙侧压力值记为测墙高度1/2处的侧压力值（筒仓仓壁最高点为深度零点，方向向下为正）。

达到稳定状态后筒仓侧壁静止侧压力沿高度方向分布与Janssen公式计算结果（取筒仓上部颗粒不平整区域重心高度为深度零点，方向向下为正）对比如图2所示。图2显示在仓体上部，模拟结果与计算结果较为吻合，在仓体下部，直径5 mm的颗粒较其他直径的颗粒产生的仓壁静止侧压力更接近Janssen公式计算值，但总体的各粒径模型的仓壁静态侧压力值与Janssen公式计算结果较为吻合。这说明，该筒仓模型可以反映实际筒仓的受力及颗粒的流动情况。

图2 静止状态下仓壁侧压力的数值模拟结果与Janssen值Fig.2 Numerical simulation results and Janssen values of lateral pressure of silo wall under static state

3 卸料过程模拟分析

3.1 流态与力链网络

在整个模型达到稳定状态后，删除筒仓底部中心的墙，开始模拟筒仓中心卸料过程。在整个卸料过程中，考虑在卸料完成不同程度时颗粒流动状态的不同，选取初始状态，卸料完成5%、25%、50%、75%时的颗粒流动状态，速度场分布及力链如图3—图5所示。

图3和图4显示，在卸料前期，上方颗粒流动状态为整体流动，在筒仓仓底附近出现混合流动；在卸料中期，筒仓内颗粒出现管状流动状态；在卸料后期，则呈现漏斗流动状态[5]。从图5可以看出，颗粒直径越大，颗粒间形成的力链网络骨架越清晰。在静止状态下，筒仓侧壁附近的力链网络随着筒仓深度的增加逐渐密集；在卸料过程中，力链网络结构不断变化，出口附近有力链拱的形成与塌落，这与Cheng等[2]的发现一致。

图3 不同直径颗粒卸料流动状态Fig.3 Flow pattern of different diameter particles during discharge

图4 不同直径颗粒卸料速度场Fig.4 Velocity field of different diameter particles during discharge

图5 不同直径颗粒卸料力链分布Fig.5 Distribution of force chains of different diameter particles during discharge

观察图3可以得出，大直径颗粒比小直径颗粒出现管状流动的时间要早。对比不同直径颗粒的流动状态图及速度云图可以看出，粒径越大，管状流动的流动区域直径就越大：粒径5 mm的流动区域直径约为0.3 m，粒径10 mm的流动区域直径约为0.4 m，粒径15 mm的流动区域直径约为0.5 m，粒径20 mm的流动区域直径约为0.6 m。对比图5可以看出，粒径越大，力链网络结构越简单。这表明对于筒仓内距离相同的两个颗粒，粒径越大，两颗粒间的力的传递越直接，因此，出口处拱的形成和塌落引起的颗粒间接触力的变化传播速度越快，影响范围越广，从而使大直径颗粒的流动区域直径比小直径颗粒的流动区域直径大。

观察图5发现，在仓底与仓壁相接处附近有力链拱的形成，拱的中部力链网络较为稀疏，拱的两端力链网络较为密集。这表明拱的中部区域内颗粒间的接触力较小，拱的两端附近的颗粒间的接触力较大。在拱中部的颗粒间的接触力随着卸料的进行迅速衰减，对比图4可以发现，拱的中部区域颗粒下落速度比拱的两端附近的颗粒下落速度大，这是因为密集的力链网络会抑制附近的颗粒的运动[2]。

对比图4和图5可以看出，筒仓侧壁附近，颗粒速度较小的区域内的力链网络比颗粒速度较大的区域内的力链网络更为密集，表明颗粒间的接触力在流动速度较小的地方比流动速度较大的地方大。这与Cheng等[2]的发现一致。卸料完成75%左右时，在筒仓底部与侧壁相接处附近会出现滞留区域，在这个区域内，力链网络一直较为密集，在其范围内的仓壁的侧压力一直较大。

3.2 卸料压力

卸料过程中，仓壁侧压力一直在不断变化，不同直径的颗粒在不同高度产生的侧壁压力随着卸料进行的变化如图6—图9所示。

图6 直径5 mm颗粒卸料过程中仓壁侧压力Fig.6 Lateral pressure of silo wall during discharge of 5 mm diameter particles

图7 直径10 mm颗粒卸料过程中仓壁侧压力Fig.7 Lateral pressure of silo wall during discharge of 10 mm diameter particles

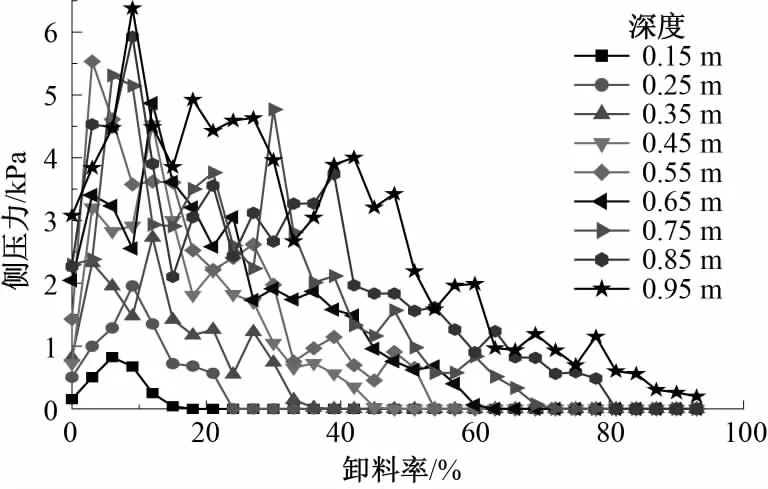
图8 直径15 mm颗粒卸料过程中仓壁侧压力Fig.8 Lateral pressure of silo wall during discharge of 15 mm diameter particles

图9 直径20 mm颗粒卸料过程中仓壁侧压力Fig.9 Lateral pressure of silo wall during discharge of 20 mm diameter particles

图6 —图9显示，不同直径颗粒在卸料过程中产生的仓壁侧压力都呈现先增大后减小的趋势，并且在增大或者减小的过程中出现震荡现象。另外，仓壁的卸料压力峰值并不是在开始卸料的瞬间出现的，而是在卸料开始一段时间之后才出现[6]。在卸料过程中，同一深度的仓壁侧压力并不是一直增大或者减小，而是在侧压力增大的过程中，会在较短的时间范围内出现侧压力减小的现象；在侧压力减小的过程中，会在较短的时间范围内出现侧压力增大的现象。对比图5可以发现，这种同一高度仓壁侧压力大小的震荡现象是由力链网络在卸料过程中的不断变化引起的。

3.3 静压力与卸料压力

各国筒仓规范对卸料压力的计算均是将静态压力乘以一个放大系数作为该高度的卸料压力值，这表明在同一高度，卸料压力峰值与静态压力有一定关系。

将图10及图11模拟结果与静态压力Janssen值和规范卸料压力进行了对比。图10显示，筒仓卸料在侧壁各个高度产生的卸料压力峰值均大于静态压力，卸料压力峰值随深度增加而增大，最大值出现在侧壁底部[8-9]。颗粒直径越大，卸料产生的卸料压力峰值越大，且基本大于规范值。图11显示卸料压力峰值约为静态侧压力的2～4倍，大于规范的超压系数Ch=2.0。

图10 模拟静压力、卸料压力、Janssen值及规范卸料压力Fig.10 Simulation static pressure,emptying pressure,Janssen value and code emptying pressure

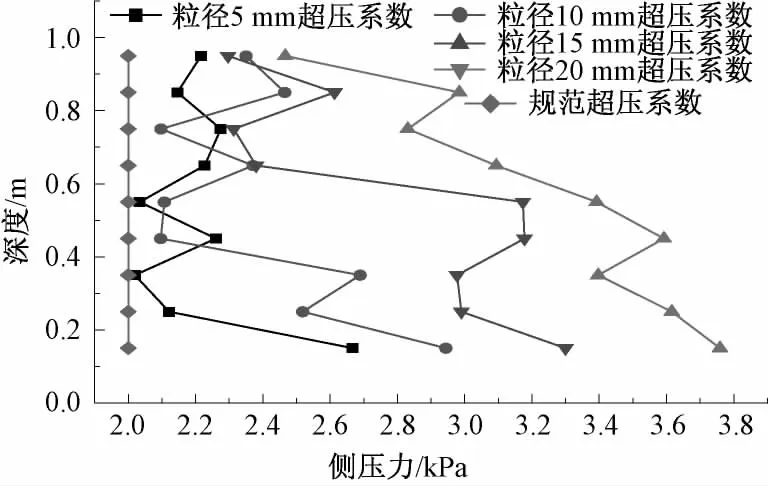
图11 超压系数Fig.11 Overpressure coefficient

从图10和图11可以看出，卸料过程中，粒径越大，仓壁受到的卸料压力峰值越大，对比图4和图5发现，这可能是因为滞留区域对流动区域产生的卸料压力有缓冲作用。对比图5发现，筒仓底部与侧壁相接点附近的力链始终比其他区域密集，表明这个区域内颗粒间的接触力比其他颗粒间的接触力大，从而导致了仓壁侧压力最大值始终出现在侧壁底端。

4 结论

本文通过对4组装有不同直径颗粒的模型仓的静态及卸料过程的模拟，并从细观尺度对模拟结果进行对比分析，得出以下结论：

（1）卸料之前，在重力作用下，颗粒间最大的接触力出现在筒仓底部附近。仓壁侧压力模拟结果与Janssen公式计算值相符。在卸料过程中，最大接触力始终出现在筒仓底部与侧壁相接处附近。如果遍历整个卸料过程的力链图和速度云图，可以明显看出颗粒间最大的接触力出现在颗粒速度最小的区域，颗粒间最小的接触力则出现在颗粒速度最大的区域。

（2）卸料过程中，密集的力链网络会抑制区域内颗粒的流动速度，使区域内颗粒流动速度减小，并使区域边缘的仓壁侧压力增大；反之，稀疏的力链网络对区域内颗粒流动速度受到的抑制作用较小，该区域内的颗粒具有较大的流动速度。

（3）筒仓侧壁受到的最大侧压力并不是在开始卸料的一瞬间出现的，而是在开始卸料一段时间之后出现的。

（4）在卸料过程中，同一高度的仓壁侧压力并不是一直增大或减小，而是在侧压力增大和减小的趋势下出现震荡现象。

（5）在相同筒仓中，颗粒直径越大，在卸料过程中产生的卸料压力峰值越大，出现的管状流动时间越早，管状流动的流动区域直径越大。

［1］ OLDAL I，SAFRANYIK F.Extension of silo discharge modelbased on discrete element method［J］.Journal of Mechanical Science and Technology，2015，29（9）:3789-3796.

［2］ CHENG Y M，CHAU K T，XIAO L J，et al.Flow pattern for a silo with two layers of materialswith dingle ordouble openings［J］.Journal of Geotechnical and Geoenvironmental Engineering，2010，136（9）:1278-1286.

［3］ 俞良群，邢纪波.筒仓装卸料时力场及流场的离散元法模拟［J］.农业工程学报，2000，16（4）:15-19.

［4］ 陈长冰，梁醒培.筒仓卸料过程的离散元模拟分析［J］.粮油食品科技，2008，16（1）:11-13.

［5］ WU J，JIANG B，CHEN J，et al.Multi-scale study of particle flow in silos［J］.Advanced Powder Technology，2009，253:62-73.

［6］ 肖昭然，王军，何迎春.筒仓侧压力的离散元数值模拟［J］.河南工业大学学报（自然科学版），2006，27（2）:10-12.

［7］ 戚迎花.散储粮储藏容重与若干影响因素的关系试验研究及离散元模拟［D］.郑州：河南工业大学，2014.

［8］ HAMMADEH H.Flow and pressure during centric and eccentric discharge in cylindrical silos［J］.Science&Technology，2012（4）:44-48.

［9］ YANG Y M， ROTTER M，OOI J，et al.Flow channel boundaries in silos［J］.Chemical Engineering Technology，2011，34（8）:1295-1302.

［10］ 曾长女，于航.基于线性接触模型的小麦三轴试验细观模拟［J］.河南工业大学学报（自然科学版），2015，36（2）:66-70.

MESO-MECHANISM OF THE EFFECT OF STORAGE PARTICLE SIZE ON THE DISCHARGE FLOW PATTERN AND LATERAL PRESSURE OF SILO

WANG Shihao，XIAO Zhaoran，LIU Kejin
（School of Civil Engineering and Architecture，Henan University of Technology，Zhengzhou 450001，China）

In the discharge process of granular materials in silo，the peak value of lateral press of silo is much greater than that of static pressure. Most of the silo engineering accidents are caused by the excessive discharge pressure. The discrete element method is used to simulate the silo discharge process in this study. Starting from the meso-particulate dispersion of storage，the effect of particle size change on the flow pattern，the force chain network and the lateral pressure on the silo wall during discharge was investigated and the internal mechanism of the influence was discussed. The results showed that the different particle size had great influence on the discharge flow state and the lateral pressure of the silo wall.The larger of the particle size，the greater of the peak value of discharge pressure，which was detrimental for the stability of the silo structure. It was found that the lateral pressure had the trend of increasing first and then decreasing，and the oscillating phenomenon was presented. Compared with the research at home and abroad，it was proved that the results of this study had reference value for practical engineering.

silo；discrete element method；meso-mechanism；flow pattern；lateral pressure

TS210.3

B

1673-2383(2017)06-0086-05

http://kns.cnki.net/kcms/detail/41.1378.N.20171226.1723.030.html

网络出版时间：2017-12-26 17:24:10

2017-04-13

河南工业大学高层次人才基金项目（150597）；国家自然科学基金项目(51178165，51708183)

王世豪（1993—），男，河南洛阳人，硕士研究生，研究方向为粮仓稳定性分析。

*通信作者