基于微课下的高中数学概念教学探究

李丽

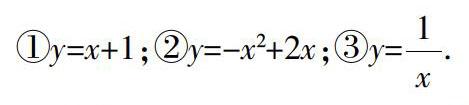
[摘  要] 数学概念贯穿于整个高中数学教学，基于微课下的高中数学概念教学能够充分调动学生参与数学课前预习的积极性，加深新概念形成的过程，大幅度提高高中学生数学概念的学习效果. 从概念形成理论、概念同化理论、有意义学习理论、发现学习理论等四个方面阐述基于微课下的高中数学概念教学策略.

[关键词] 微课;高中数学;概念教学

数学概念是推导数学定理、公式以及法则的基础，是解决数学问题的必要条件. 而数学概念抽象性较强，在较短时间内学生很难理解数学概念的真正意义，常常把题目做错归咎于“计算出错”、“计算粗心大意”等等，忽视了数学概念在解题中的关键作用. 自2012年教育部教育管理信息中心实施微课比赛以来，笔者开始在高中数学概念教学中引入微课，不仅构建了以学生为中心的课堂教学，而且引导学生追本溯源，了解具体数学概念产生的背景、形成过程，从本质上促进学生理解和掌握数学概念.

概念形成理论下的高中数学概念微课教学

概念形成是以学生的直接经验为前提，在对各种例证和客观事物反复感知抽象、比较和分析的基础上，以归纳的方式形成数学概念的一种方式. 例如在学习“函数单调性”时，教师应创设概念学习情境，通过学生熟悉的实际生活问题引入课题，充分调动学生主体参与的积极性. 在具体教学实践中，笔者从学生熟悉的生活情境引入，设计了以下微课内容：

四川省某市2017年1月1日24 小时内的气温变化如图1所示，请仔细观察这张气温变化图，回答以下问题.

①随着时间的变化，气温是如何变化的？

②随着时间的增长气温逐渐升高，这句话应用数学语言如何表示？

③在8时至18时，气温是否随着时间的增大而增大？

设计意图：通过观察不同时间内气温的变化，初步感受气温增减的趋势，为函数单调性的定义打下基础. 同时，将学生对气温升降的感性认识逐渐上升为函数图像增减性的理性认识，揭示了函数单调性最为本质的东西，有利于增函数、减函数等定义的自然生成.

又如，在微课设计中，教师注重新知和旧知之间的联系，给出了以下函数式：

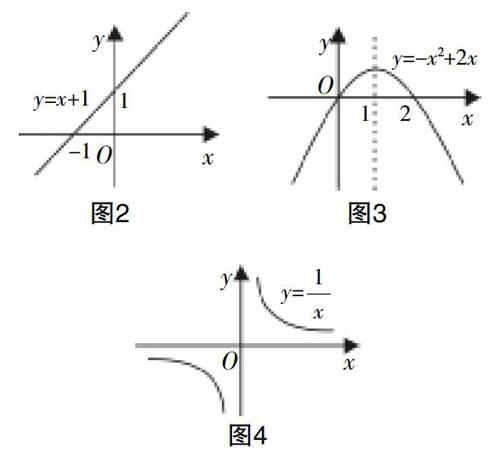
要求学生描绘出上述函数图像，亲自体会不同区间内函数的升降趋势，通过观察图像，如图2、图3、图4所示，让学生自主分析，得出函数单调性的初步概念，将原本十分抽象的函数单调性概念具体化，激发了学生学习的兴趣.

概念同化理论下的高中数学概念微课教学

概念同化是以学生的间接经验为前提，利用学生已经掌握的数学概念和知识经验或原有认知结构去学习新的数学概念，从而完善学生认识结构的过程. 值得一提的是，这种概念同化必须具备两个条件，一是新概念必须具有逻辑意义;二是学生原有认知结构中必须具备同化新概念的知识经验.

例如学习映射概念时，学生已经学习了函数的概念，此时，教师可以利用微课加深函数与映射这两个数学概念之间的区别和联系. 在具体教学实践中，笔者设计了以下微课内容：

首先回顾函数的概念，通过以下案例要求学生总结出这些对应具有什么特点，为即将学习的映射概念做铺垫.

①对于每一个三角形都有唯一的面积与之对应;

②班级中的每一个学生都有唯一的座位与之对应;

③对于任意有序实数对在直角坐标系中都有唯一的点与之对应.

设计意图：通过已经学习过的函数知识，结合所列举的例子，让学生自己总结出对应规律，初步了解映射的特殊情况.

其次，列举如下对应关系，并回答以下问题.

①例子中的“唯一”是什么意思.

②在上述三组图像中，如果第一、二组中的对应我们称之为映射，请概括出映射的定义.

③映射与函数之间是什么关系.

设计意图：利用图组的形式，通过类比归纳出映射的含义.

最后，联系生活实际，列举出现实生活中含有映射的实例.

设计意图：强化训练，深刻感知映射的概念.

有意义学习理论下的高中数学概念微课教学

有意义学习是在原有认知结构的基础上，在新观念和原有认知上建立非人为和实质性的联系，从而帮助学生形成新的认知结构过程，其中，原有的认知结构对于新概念的学习始终是一个最为关键的因素.

例如，在高中函数学习中，函数的概念至关重要，对其能否真正理解直接关系着三角函数等知识的学习，然而，对于初次接觸函数概念的学生来说，抽象性较强，这就要求教师充分利用学生已有的认知结构，构建有意义的学习. 在具体教学实践中，笔者设计了以下微课内容.

首先，引导学生回顾初中数学中函数的定义和表示方法，并设计出学生骑自行车上学的情景，要求学生说出该实例中涉及哪些变量，这些变量之间有什么样的关系.

设计意图：通过引入初中函数的定义和学生熟悉的生活实例，引导学生理解描述变量之间关系的数学模型就是函数，为高中函数概念的有意义学习打下基础.

其次：设立探究任务，导入新课，请学生思考以下问题，根据初中函数的定义，总结出函数的概念.

①图6是1979-2001年南极上方臭氧层空洞的面积，该例子中涉及哪些变量，变量之间有什么关系？

②一枚炮弹发射26 s后击中目标，已知炮弹的射高为845米，且炮弹发射后的时间t与炮弹距地面的高度h符合h=150t-t2，请问t和h之间有什么关系？

③表1是2006-2015年中国城镇居民家庭恩格尔系数，请问年份和恩格尔系数之间存在着什么关系？

设计意图：以上3个实例均是函数关系的对应，有利于知识的正向迁移，并鼓励学生通过观察、分析、对比、归纳出对应关系在函数概念中的作用，培养学生分析问题、提取信息和抽象思维的能力，启发学生思考探究，促进学生有意义学习.

发现学习理论下的高中数学概念微课教学

发现学习理论认为只有在具体情境中，学生才能在发现和亲身体验过程中获得最有价值的知识和能力，因此，在数学概念教学中，教师必须重视知识的发生过程，设计和制定各种问题情境，让学生在独立思考和自主探究的过程中加深对数学概念的理解.

例如在“集合的基本运算”学习时，教师可以类比子集概念的发现过程，鼓励学生自己发现问题.笔者在组织学生学习交集、并集概念时，设计了以下微课内容.

首先，回顾旧知，引发问题. 通过提示性的语言或挖空的方式回顾子集和集合相等的数学概念，引导学生思考实数之间除了比较大小外，还常常进行实数的加减，那么两个集合能否“加减”了？

设计意图：通过回顾旧知，类比子集概念的生产过程，并联系实数的加减运算，为交集和并集的概念打下基础.

其次，类比加法运算，归纳并集和交集的数学概念.笔者设计了以下几个集合，要求学生归纳出集合A、集合B、集合C之间的关系.

①A={xx是有理数}，B={xx是无理数}，C={xx是实数}.

②A={1，3，5，7}，B={2，4，6，8}，C={1，2，3，4，5，6，7，8}.

设计意图：通过类比熟悉的加法运算，归纳出上述两个例子的共同点，为并集概念奠定基础.

观察下面几个集合，归纳出集合A、集合B、集合C之间的关系.

①A={直角三角形}，B={等腰三角形}，C={等腰直角三角形}.

②A={2，3，5，7，8}，B={1，4，6，8}，C={8}.

设计意图：通过寻找集合A、集合B、集合C之间的关系，归纳出集合C既属于集合A，又属于集合B，为交集概念奠定基础.

最后，归纳总结，回顾前面集合C和后面集合C之间的联系与区别，从数学概念的本质上进行分析.

综上所述，数学概念贯穿于整个高中数学教学，基于微课下的高中数学概念教学能够充分调动学生参与数学课前预习的积极性，加深了新概念形成的过程，大幅度提高了高中学生数学概念的学习效果.