高中数学人教A版、B版教材习题的认知水平比较
覃淋
[摘 要] 对高中数学人教A版、B版教材“统计与概率”部分习题的数学认知水平进行比较,研究发现:水平3——迁移性理解水平的题目,A版教材和B版教材所占比例相差不大;水平1——操作性记忆水平的题目,二者占比相差较大,B版教材较A版教材多了15.6%;水平2——概念性理解水平的题目,A版教材比B版教材多了9.6%;A版教材在水平4的习题类型比B版教材丰富,数量也比B版教材多.
[关键词] 数学教材;统计与概率;认知水平;比较
数学教材是“课程标准”理念的体现,一般是由正文、例题、习题三部分有机组成的. 例题、习题作为中学数学教材的重要组成部分,例题、习题的设置在某种程度上反映了教材的特征和教材编写者的价值取向,在教材中的重要性不言而喻. 数学家哈尔莫斯认为,问题是数学的心脏;波利亚也指出“中学数学的首要任务就是加强解题训练”“掌握数学就意味着善于解题”. 因此,对数学教材中的例题、习题进行研究是数学教材研究的中心问题之一.
教材作为教师教授、学生学习的主要依据,而不同教材中的习题安排又是不同的,那么对一线数学教师来说,应该怎样去选择一本合适的教材呢?不同版本的教材其习题设置与安排又各有什么特点呢?哪种教材习题的安排更有利于学生学习,更有利于培养学生的能力呢?为此,我们选取了在我国使用范围较广的人民教育出版社出版的A版、B版高中数学教材,以教材中“统计与概率”部分的习题为对象进行比较,考察两套教材“统计与概率”部分习题的数学认知水平.
两套教材都是4章,“统计与概率”各2章,主要包括[1-4]:随机现象、分层抽样、系统抽样、标准差、频率分布、随机事件、互斥事件、古典概型、几何概型、随机变量的均值与方差、超几何分布、二项分布、正态分布、条件概率、相互独立事件、独立性检验、回归分析等内容.
一般而言,中学数学教材中的习题分为“练习题、习题和复习题”三类.其中,练习题主要涉及单一的概念、定理、命题以及相关运算法则等,主要作用是教师课堂教学使用,使学生熟悉相关教学内容;习题和复习题则涉及多个知识点,主要用于加深学生对“双基”的理解,巩固和掌握知识、基本技能和一些重要的数学思想方法等[5]. 本文统计的习题包括例题、练习题、习题和复习题四类,下文在未做特别说明的情况下,本研究中的习题是“例题、练习题、习题和复习题”的统称.
數学习题的认知水平框架
20世纪50年代,布鲁姆主编的《教育目标分类学·认知领域》将认知目标具体分为“知识、领会、运用、分析、综合、评价”6个水平. 这时,布鲁姆提出的关于“认知目标”的分类还是关于一般教育学的,并不是针对数学学科的.后来有学者对此进行进一步的研究,把布鲁姆的“认知目标分类”引入了数学学科,并设计了“计算、领会、运用、分析”4个层次的认知水平目标,但该分类方法在“连续性与层次性方面存在不足”[6]. 顾泠沅等在此基础上,通过大样本测试,将数学认知水平分为以下4个层次[7]:水平1:计算——操作性记忆水平;水平2:概念——概念性记忆水平;水平3:领会——说明性理解水平;水平4:分析——探究性理解水平.
在此研究基础上,结合“统计与概率”部分习题的特点以及课程标准对“统计与概率”内容的要求,我们将“统计与概率”部分的习题的数学认知水平分为以下4个层次,水平1:计算——操作性记忆水平;水平2:概念——概念性理解水平;水平3:应用——迁移性理解水平;水平4:分析——综合性探究水平.
进一步,水平1为记忆水平,我们称为低认知水平;水平2和水平3为理解水平,我们称为一般认知水平;水平4为分析综合水平,我们称为高认知水平.
根据学生解决高中数学教材中相关数学问题所必须达到的数学认知要求,我们结合教材中相关习题对数学认知水平分析框架做出如下界定.
水平1:计算——操作性记忆水平.该水平的习题对学生的数学认知水平要求最低,只要按照课本要求的程序或方法进行基本计算就可以解答这类问题;或直接代入相关数学公式就可以解决,只要求记住解题程序或步骤,不要求学生理解运算背后的数学原理.这里,我们把简单的计算题、作图题、概念记忆题归为水平1. 如例题“在某年级的联欢晚会上设计了一个摸奖游戏,在一个口袋中装有10个红球和20个白球,这些球除颜色不同外其他完全相同. 一次从中摸出5个球,至少摸到3个红球就中奖,求中奖的概率”,练习题“从一副不含大小王的52张扑克牌中任意抽出5张,求至少有3张A的概率”,这里学生按照教科书中给出的方法进行基本计算即可.
水平2:概念——概念性理解水平.要求学生能初步理解教材中的基本概念、原理、方法,我们把举例题、论述题归入水平2. 如“给出一个概率很小(大)的随机事件的例子”,又如“一个骰子掷一次得到2的概率是1/6,这说明一个骰子掷6次一定会出现一次2,这种说法对吗?说说你的理由”.
水平3:应用——迁移性理解水平.解决这类问题要求学生能够理解数学原理、思想与方法,并能解决一些实际问题.需要学生对运算、概念有比较彻底的理解,并有一定的迁移能力. 这里我们把较为复杂的解答题或是教材中没有类似例题的解答题归入水平3. 如“收集1993年至2002年每年中国人口总数的数据,建立人口与年份的关系,预测2003年和2004年的人口总数,并计算与实际数据的误差”.
水平4:分析——综合性探究水平. 解答该水平的习题需要学生具备高层次的数学认知水平,对问题进行具体分析,能创造性地解决没有接触过的非常规的问题,同时还要求对问题的解决过程或方案做出价值判断,也就是数学家解决相关问题时所达到的水平. 这里,我们把开放题、调查类题、证明题归入水平4. 如“设事件A,B,C满足条件P(A)>0,B和C互斥,试证明:P(B∪CA)=P(BA)+P(CA)”,又如“收集班上所有学生身高的数据,构造一个关于每一个学生的性别与其身高是否高于(或低于)中位数的列联表,并讨论能否在犯错误的概率不超过0.01的前提下认为性别与身高有关系”.
统计结果
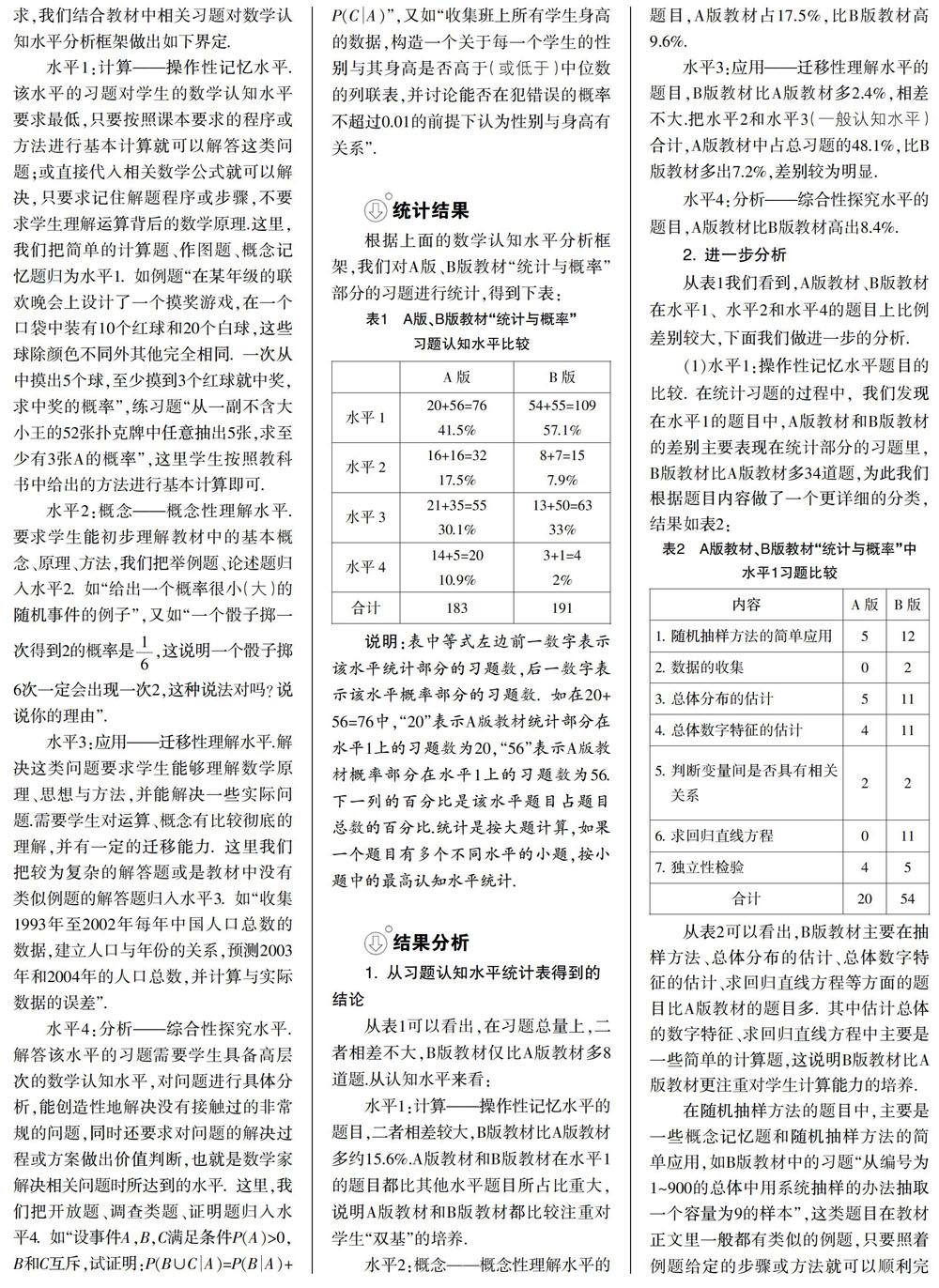
根据上面的数学认知水平分析框架,我们对A版、B版教材“统计与概率”部分的习题进行统计,得到下表:
说明:表中等式左边前一数字表示该水平统计部分的习题数,后一数字表示该水平概率部分的习题数.如在20+56=76中,“20”表示A版教材统计部分在水平1上的习题数为20,“56”表示A版教材概率部分在水平1上的习题数为56. 下一列的百分比是该水平题目占题目总数的百分比.统计是按大题计算,如果一个题目有多个不同水平的小题,按小题中的最高认知水平统计.
结果分析
1. 从习题认知水平统计表得到的结论
从表1可以看出,在习题总量上,二者相差不大,B版教材仅比A版教材多8道题.从认知水平来看:
水平1:计算——操作性记忆水平的题目,二者相差较大,B版教材比A版教材多约15.6%.A版教材和B版教材在水平1的题目都比其他水平题目所占比重大,说明A版教材和B版教材都比较注重对学生“双基”的培养.
水平2:概念——概念性理解水平的题目,A版教材占17.5%,比B版教材高9.6%.
水平3:应用——迁移性理解水平的题目,B版教材比A版教材多2.4%,相差不大.把水平2和水平3(一般认知水平)合计,A版教材中占总习题的48.1%,比B版教材多出7.2%,差别较为明显.
水平4:分析——综合性探究水平的题目,A版教材比B版教材高出8.4%.
2. 进一步分析
从表1我们看到,A版教材、B版教材在水平1、水平2和水平4的题目上比例差别较大,下面我们做进一步的分析.
(1)水平1:操作性记忆水平题目的比较. 在统计习题的过程中,我们发现在水平1的题目中,A版教材和B版教材的差别主要表现在统计部分的习题里,B版教材比A版教材多34道题,为此我们根据题目内容做了一个更详细的分类,结果如表2:
从表2可以看出,B版教材主要在抽样方法、总体分布的估计、总体数字特征的估计、求回归直线方程等方面的题目比A版教材的题目多. 其中估计总体的数字特征、求回归直线方程中主要是一些简单的计算题,这说明B版教材比A版教材更注重对学生计算能力的培养.
在随机抽样方法的题目中,主要是一些概念记忆题和随机抽样方法的简单应用,如B版教材中的习题“从编号为1~900的总体中用系统抽样的办法抽取一个容量为9的样本”,这类题目在教材正文里一般都有类似的例题,只要照着例题给定的步骤或方法就可以顺利完成,这类题目主要是加强学生对一些基本概念的理解.
在总体分布的估计中,主要是作图类题目,一般是给出一堆数据,然后要求作出直方图、茎叶图等,是非常基础性的题目.
因此,可以说,在“统计与概率”部分,B版教材比A版教材更加注重强调对基础知识的掌握,更加强调对基本技能的培养.
(2)水平2:概念性记忆水平题目的比较. 水平2主要是举例题和论述题,这类题目都要求学生对基本概念和原理有一定的理解. 其中A版教材的举例题和论述题各有10题、22题;B版教材的举例题与论述题各有2题、13题,A版教材在水平2的习题数量远大于B版教材,说明A版教材比B版教材更加注重学习对知识的理解,即是说,在“统计与概率”部分,A版教材比B版教材更好地体现了课程标准的理念.
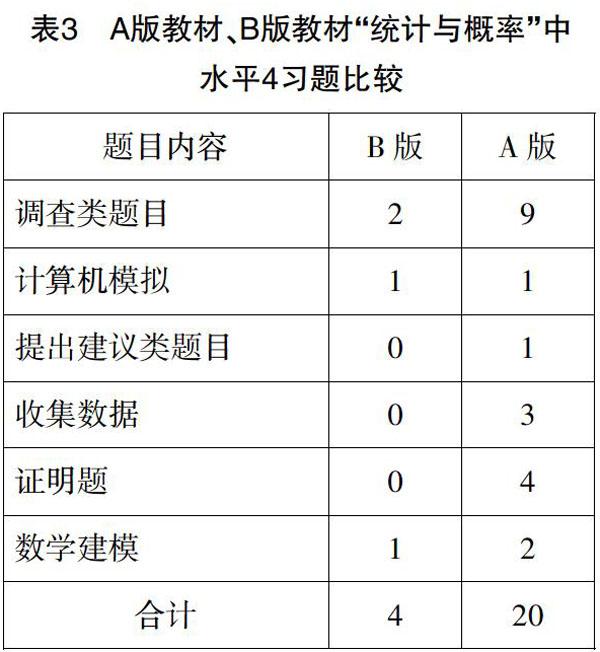
(3)水平4:综合性探究水平题目的比较. 和水平1不同,B版教材在水平4的题目极少,仅占2%,可以忽略不计. 下面是我们根据习题内容进行的详细分类.
从表3可以看出,在水平4的题目中A版教材比B版教材题目类型更为丰富. 调查类题目A版有9道,B版教材仅有2道.B版的2道分别是设计调查问卷和设计调查问题,A版教材主要有:设计调查方案、设计抽样方案、设计调查问卷、设计提问方法等,类型较B版教材更丰富.
在收集数据的题目中,A版教材有3个题目,这些题目都和学生的生活比较接近,也是学生比较感兴趣的. 如其中一个题目就是让学生统计全班同学的生日,然后计算生日所在月份的频率和频数. 证明题是培养学生逻辑思维能力的很好的载体,但在B版教材中,统计概率部分没有一个证明题!
结论
通过以上对A版教材和B版教材的比较,可以得出以下结论:
(1)A版教材、B版教材在习题总量上相差不大,B版教材稍多于A版教材;而实际上,从习题的类型看,B版教材在例题数量上远多于A版教材,但在练习题、习题和复习题上则远少于A版教材.
(2)A版教材、B版教材的习题在低认知水平(水平1)上相差较大;同时两套教材在水平1的题目是最多的,都远高于其他三个水平的题目数量,说明我国教材还是注重对学生“双基”的培养. A版教材、B版教材都非常重视教材中的基础知识,B版教材尤为注重;同时,在对学生计算能力的培养上,B版教材也比A版教材更为重视.
(3)A版教材、B版教材的习题在较高认知水平(水平2和水平3)上相差不大,各占习题总量的47.6%、40.7%,A版教材稍多于B版教材. 在高认知水平(水平4)上,两套教材的习题都比较少,其中B版教材仅有4道题目;从所占比例来看,A版教材高认知水平的题目有20%,B版教材仅有2%. 因此,在对学生能力的培养上,A版教材显然比B版教材做得更好一些,B版教材在高认知水平上的题目过少,对学生的创造性解决问题的能力的培养有所不足. 当然这并不是说,A版教材在这一方面做得很好.
从对学生创新思维的培养来说,我国的教材还存在着较大不足. 虽然在国际上许多测试(如PISA、TIMSS测试)中,我国学生都能拿高分. 但一些研究也表明[8],中国学生在计算题、常规问题和条件受限问题解决上远高于美国学生,但在解决开放问题时却弱于美国学生. 顾泠沅的研究也表明:我国学生在计算和概念层面的水平已大幅度提高,但分析问题和解决问题的能力竟有所下降[9].因此,如何在保持“双基”优势的基础上,进一步培养我国学生的创新思维能力是摆在我国数学教育面前的一个大问题.
我国数学教育一向重视基础,注重概念,这是必要的,但在“统计与概率”内容中不应对“概念”过于强调,要“淡化形式,注重实质”. 在适当增加习题数量的基础上,适当地减少低认知水平习题所占比例. 同时把概念性理解题目的形式作适当变化,降低和例题形式完全相同的习题比例,增加一些变式概念性练习. 在教材中尤其应该适当地增加一些高认知水平的习题,多设置一些非常规、开放性的问题,以此来发展学生解决数学问题的能力,培养学生提出猜想、构造模型,一般化,数学推理证明等高水平认知能力.
参考文献:
[1] 课程教材研究所,中学数学课程教材研发中心. 普通高中课程标准实验教科书A版数学3(必修)[M]. 北京:人民教育出版社,2011.
[2] 课程教材研究所,中学数学课程教材研发中心. 普通高中课程标准实验教科书A版数学选修2-3 (必修)[M]. 北京:人民教育出版社,2011.
[3] 课程教材研究所,中学数学教材实验研究组. 普通高中课程标准实验教科书B版数学3(必修)[M]. 北京:人民教育出版社,2011.
[4] 课程教材研究所,中学数学教材实验研究组. 普通高中课程标准实验教科书B版数学选修2-3(必修)[M]. 北京:人民教育出版社,2011.
[5] 吕世虎,孙学敏. 中国与新加坡初中数学教材中概率习题的比较研究[J]. 数学教育学报,2010,19(6):70-73.
[6] 高文君,鲍建生. 中美教材习题的数学认知水平比较——以二次方程及函数为例[J]. 数学教育学报,2009,18(4):57-60.
[7] 沈兰,郑潤洲. 变革的见证[M]. 上海:上海教育出版社,2008.
[8] 蔡金法. 中美学生数学学习的系列实证研究[M]. 北京:教育科学出版社,2007.
[9] 上海青浦实验研究所. 关于教学目标因素分析的数据报告:以上海青浦区数学学科为例[J]. 教育发展研究,2007(7-8):78-83.

