一类无圈型Nakayama代数的量

沈萍,陈正新

(福建师范大学数学与信息学院,福建 福州 350117)

一类无圈型Nakayama代数的量

沈萍,陈正新

(福建师范大学数学与信息学院,福建 福州 350117)

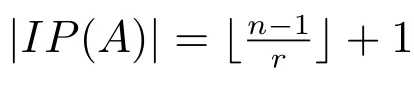
Nakayama代数;同调方法;代数的量

1 引言

在数学的许多领域,都存在关于给定对象大小的度量,如集合具有基数,向量空间具有维数,拓扑空间具有欧拉示性数等等.最近文献[1]定义了具有广泛存在性的富化范畴的量.富化范畴是满足附加条件的单位半群范畴(或称为张量范畴),要求其对象之间的Hom集不再是集合,而是原单位半群范畴中的对象.具有有限个对象的富化范畴的量是与其对象之间的Hom集相联系的矩阵的逆矩阵中所有元素的和.在此框架下,拓扑空间的欧拉示性数、偏序集的M¨obius逆、度量空间的Minkowski维数等都与富化范畴的量密切相关,参见文献[1-3].事实上,许多度量几何和图论中经典数量也与富化范畴的量密切相关,数学工作者们相信并期待富化范畴的量在更多数学分支中得到应用与发展,本文着重介绍富化范畴的量在域上有限维结合代数研究中的应用,其他的不做赘述.本文介绍域上具有有限总体维数的有限维代数的量的定义,并求出了一类特殊Nakayama代数的量.对域k上总体维数有限的有限维代数A,它的所有不可分解投射模构成了一个富化范畴,记为IP(A),称富化范畴IP(A)的量为代数A的量.由于所有A-模都是投射A-模的同态像,而投射A-模总是所有不可分解A-模的直和的直和项,因此富化范畴IP(A)是A-模范畴中的重要构成部件.又由于所有不可分解投射A-模之间的Hom空间的维数恰好构成了代数A的Cartan矩阵,参见文献[4],因此代数A的量(或富化范畴IP(A)的量)又可定义为代数A的Cartan矩阵的逆矩阵的所有元素求和,参见下面的定义.根据文献[2]的主定理,我们也可以用同调方法计算代数的量.本文在文献[2]的主定理的基础上,计算一类Nakayama代数的单模之间同调群的维数,从而求出该Nakayama代数的量.

2 基本定义与记号

下面设k为代数封闭域,A为总体维数有限的有限维k-代数.本文中所有A-模均为左A-模,modA为全体有限维左A-模构成的模范畴.记{Si|i=1,2,···,n}为单A-模的全体,Pi(分别地,Ii),i=1,2,···,n,为Si对应的不可分解投射(分别地,内射)模.Pd Si(分别地,Id Si)表示单模Si的投射 (分别地,内射)维数.对正整数i,j,若i＜j,记 [i,j]表示集合{i,i+1,···,j−1,j}.记表示向下取整函数,如

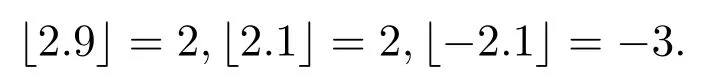
令

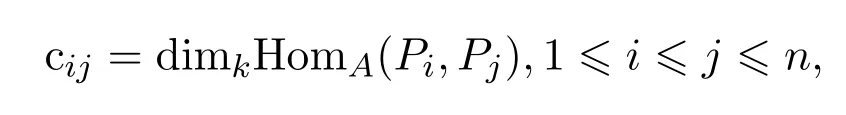
n阶矩阵C=(cij)n×n,称C为代数A的Cartan矩阵.

定义 2.1设A为总体维数有限的有限维k-代数,称代数A的Cartan矩阵的逆矩阵的所有元素和为代数A的量,记为|IP(A)|.

定义 2.2[5]设M∈modA,若M的所有子模的集在包含关系下是线性有序的，即对M的任意两个子模N和N′,或者N⊂N′,或者N⊃N′,则称M是单列模.

定义 2.3[5]如果每一个不可分解投射右(左)A-模是单列模,则称代数A是右(左)序列的.如果代数A既是左序列的又是右序列的,则称代数A为Nakayama代数.

由文献[5]定理3.2知,Nakayama代数可分为两类,一类为底图有圈的,另一类是底图无圈的.本论文研究一类特殊的无圈型Nakayama代数A的量,A=kQ/I,其中箭图Q为如下的线性箭图:

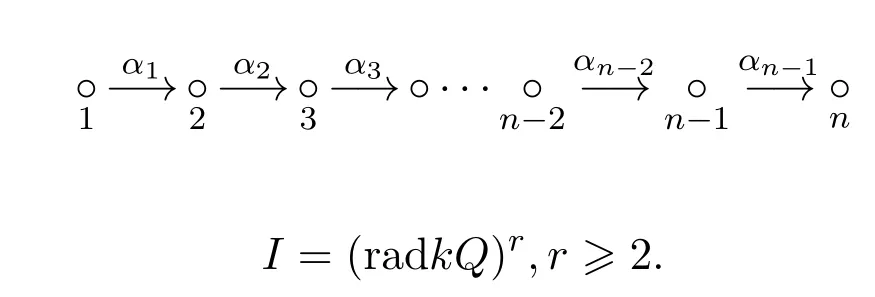
换句话说,I是kQ中由路长为r的所有路

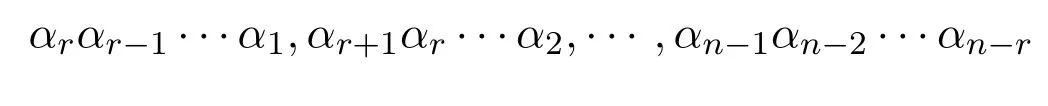
所生成的理想.

本文以下部分中代数A总为上述Nakayama代数.对i≤j,由于Nakayama代数A中具有给定的socleSj及topSi的不可分解模是唯一的,可记该不可分解模为m(i,j),

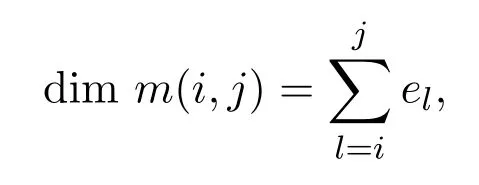
这里el表示第l个分量为1,其余分量为0的n维向量.

3 一些引理

由单列模的性质,对不可分解A-模N,其投射盖Pi1一定为不可分解模.令f:Pi1→N为投射盖,可得kerf为不可分解模,因此可得下面的引理3.1.

引理 3.1设M,N为不可分解模,若存在正合列

其中Pit,t=1,2,···,s,为不可分解投射模,则

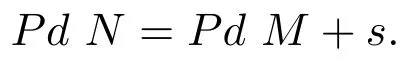
引理 3.2[6]设0→B→P→C→0为A-模中的正合列,其中P为投射A-模,则对任意的l≥1及A-模M,有

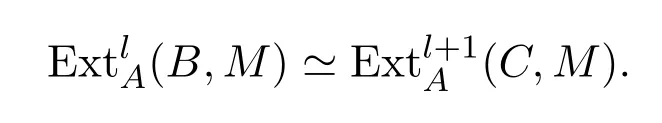
证明对正合列

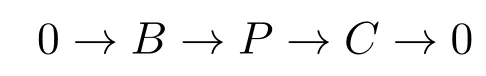
用函子Hom(−,M)作用,得到长正合列:

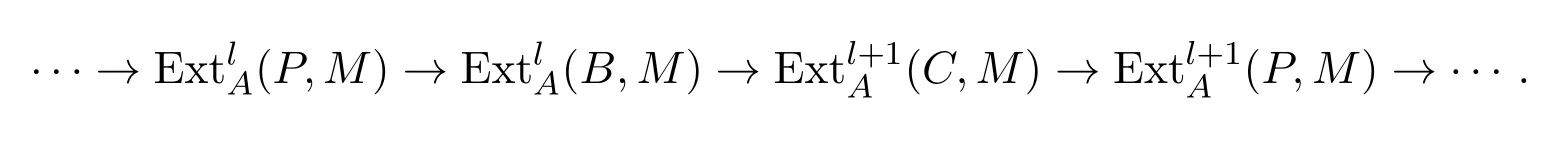
因为P为投射A-模,所以,从而有

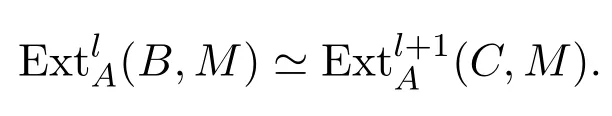
对偶地,可证如下引理:

引理 3.3设0→B→I→C→0为A-模中的正合列,其中I为内射A-模,则对任意的l≥1及A-模M,有

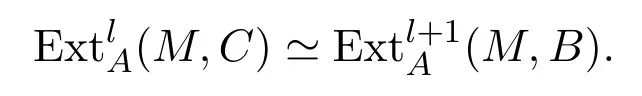
引理 3.4对任意的i=1,2,···,n,及非负整数t,若tr+i≤n,则

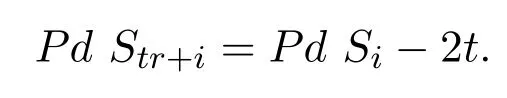
证明对t用数学归纳法.

当t=1时,有

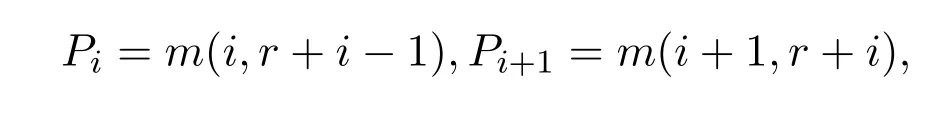
从而得到

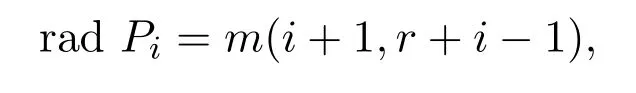
因此有下面的正合列:

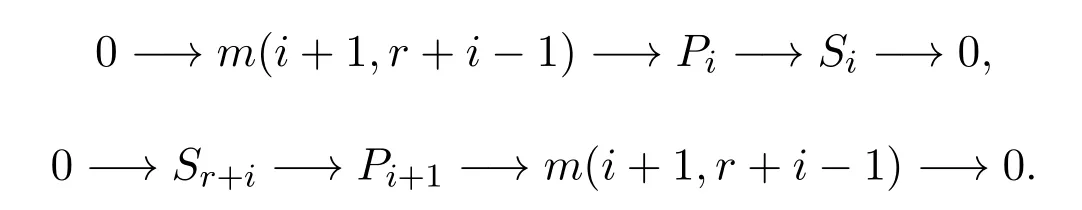
从而有正合列:

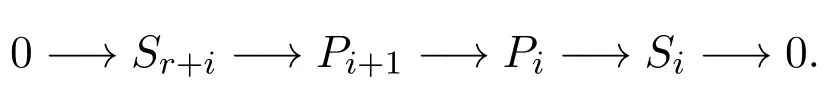
再由引理2.1得

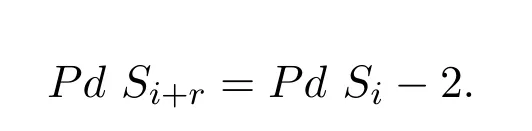
假设等式

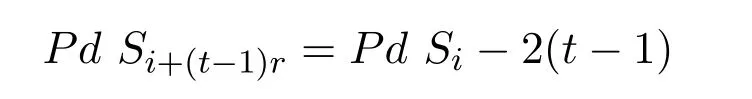
成立.下证等式

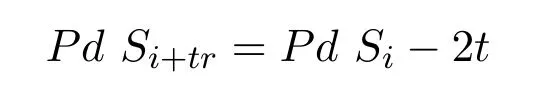
也成立.此时

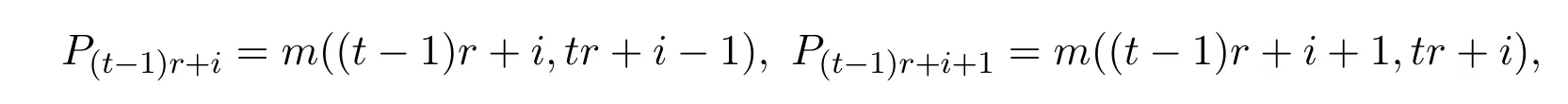
并且

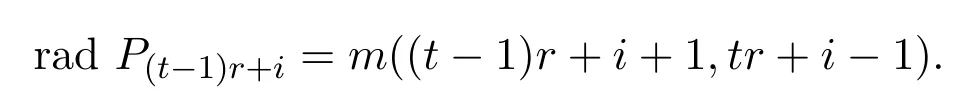
于是有下面两个正合列:

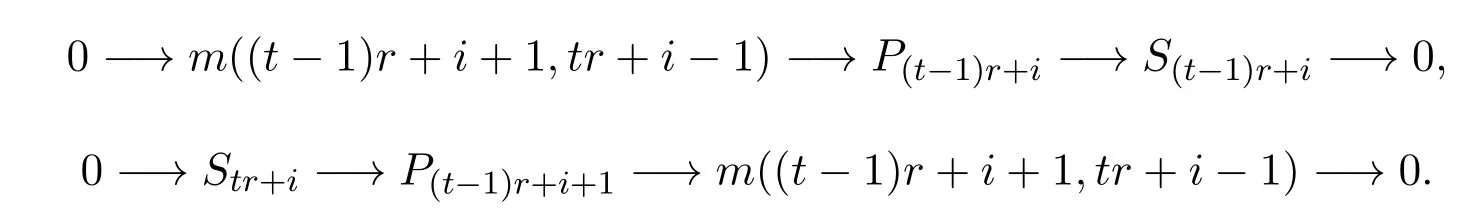
从而有正合列:

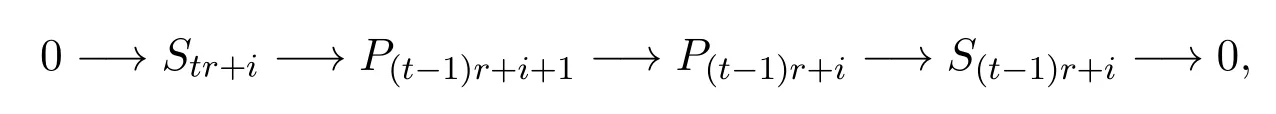
故有

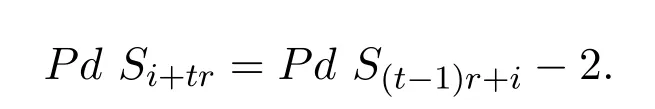
又由归纳假设知

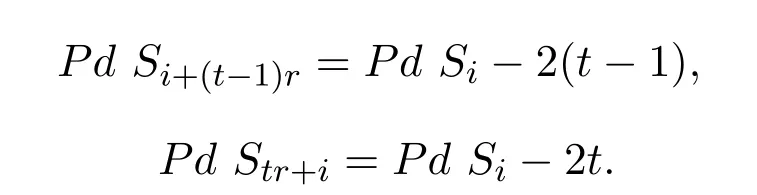
从而

对偶地,可证如下关于内射维数的引理:

引理 3.5对任意的i=1,2,···,n,及非负整数t,若tr+i≤n,则

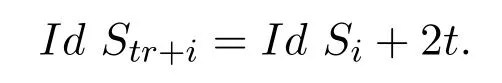
由Nakayama代数的性质及引理3.1,可证如下引理：

引理 3.6对任意的非负整数l,当i＞j时,有

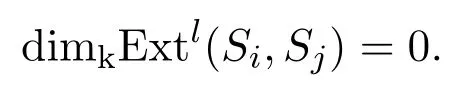
证明设Pd Si=r.若l＞r,则

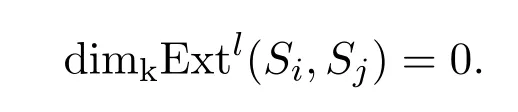
若l=0,

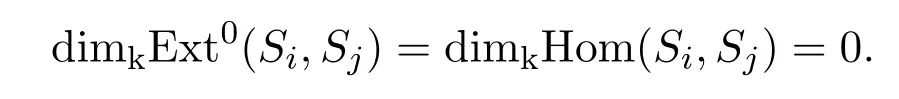
若1≤l≤r,令Si的投射分解式为:

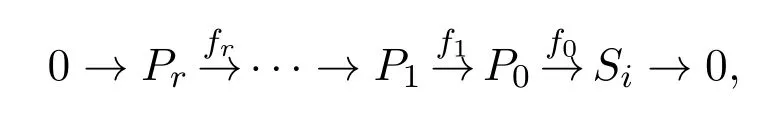
Ki=kerfi,0≤i≤r,则

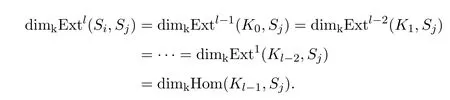
因为τi−j(Sj)=Si,则根据直向代数的性质

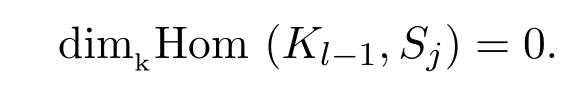
因此

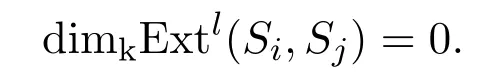
引理 3.7若j−i=tr,,则,且对任意l/=2t,

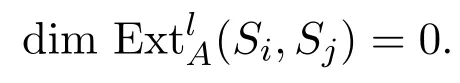
证明对t用数学归纳法.

当t=1时,有j−i=r,j=r+i,易知存在如下短正合列:

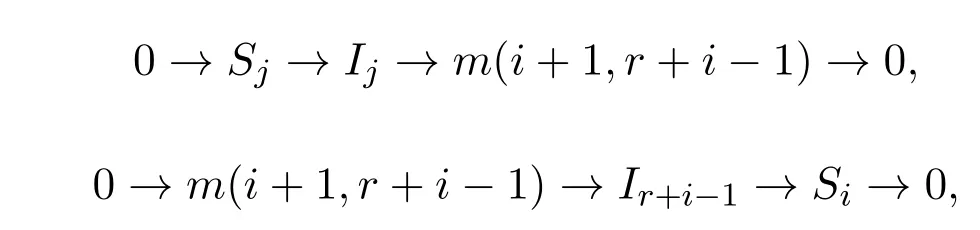
得到正合列:

故有

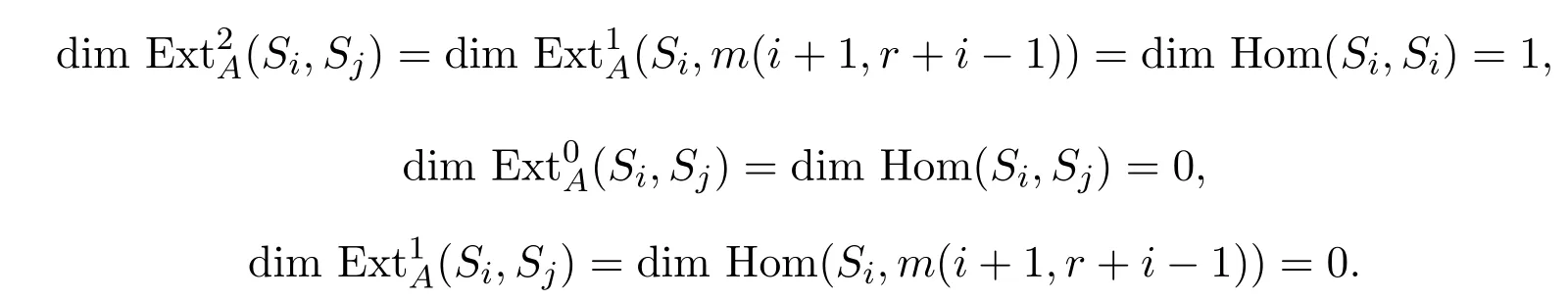
由引理3.6及上面的正合列知,对任意的l≥3,

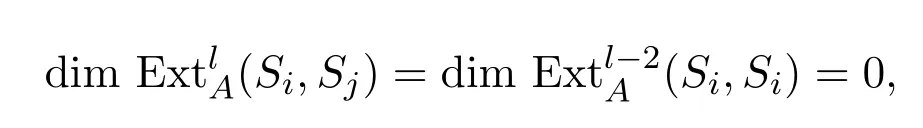
这就证明了此时引理成立.

假设当j−i=(t−1)r时,等式

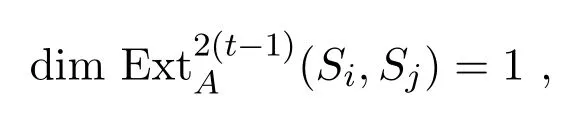
且对l/=2t−2,

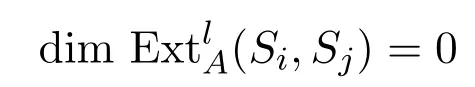
成立.下证:j−i=tr时,等式,且对l/=2t,也成立.易知存在如下短正合列:

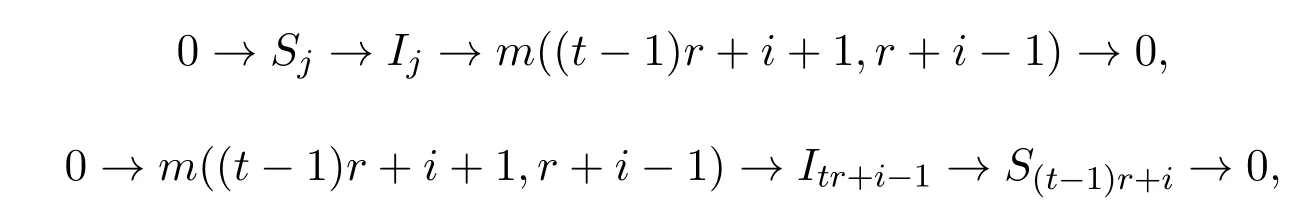
于是有如下正合列:

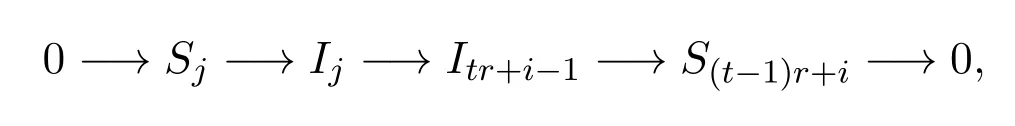
故有

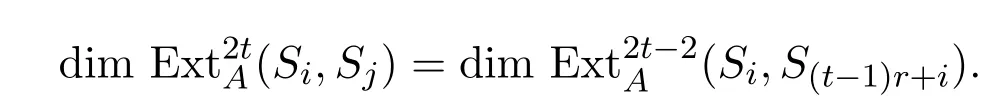
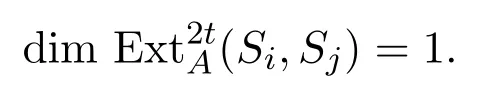
当l/=2t时,同理有

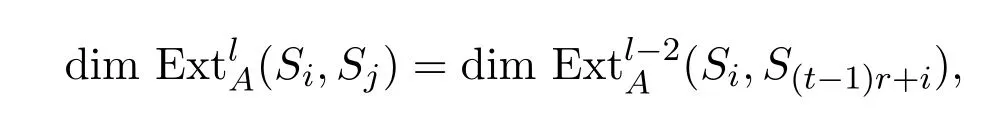
由归纳假设知,

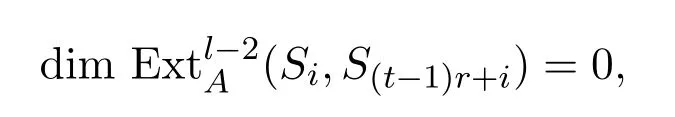
引理 3.8若j−i=tr+1,,则

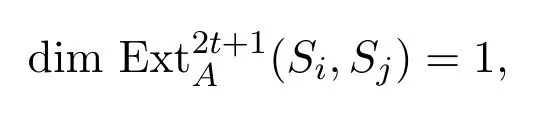
且对任意l/=2t+1,.

证明对t用数学归纳法.

若t=0时,则j=i+1.下面对j∈[2,n]分以下两种情形证明引理成立.

情形 1j∈[r+1,n].此时，Ii=m(i−r+1,i),Ii+1=m(i−r+2,i+1),易知存在如下短正合列

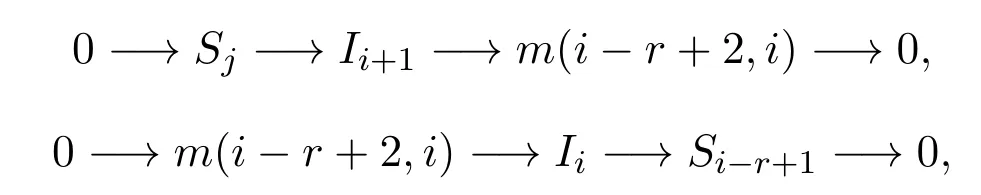
所以

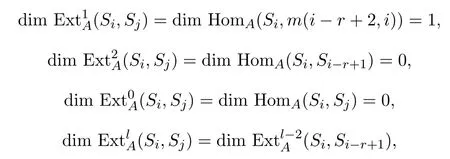
对任意的l≥3.因为r≥2,i−r+1＜i,从而由引理3.6知.故引理成立.

情形 2j∈[2,r].

此时Id Sj=1,从而,l≥2,易知存在如下短正合列:

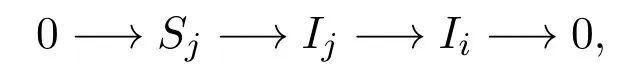
则

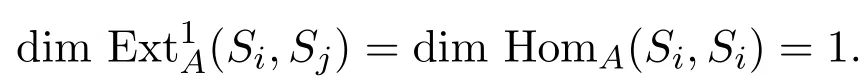
这就证明了此时引理成立.

假设j−i=tr+1时,等式,且对任意的l/=2t+1,

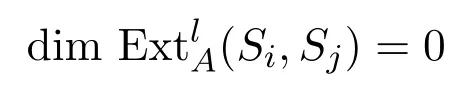
成立.下设j−i=(t+1)r+1.易知存在如下短正合列:

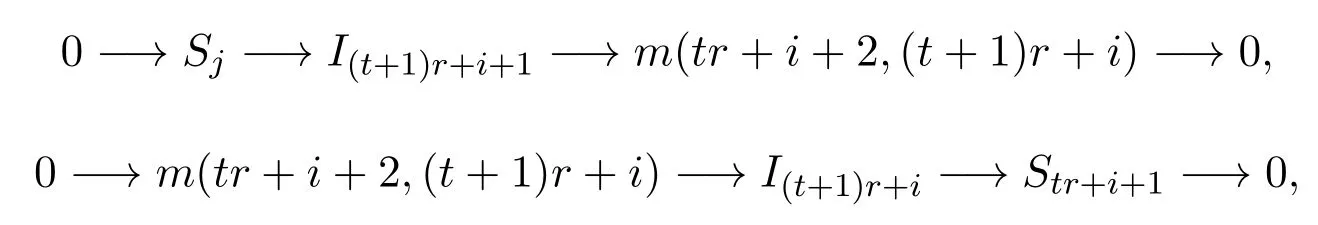
得到正合列:

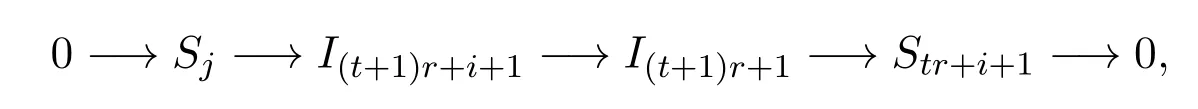
从而

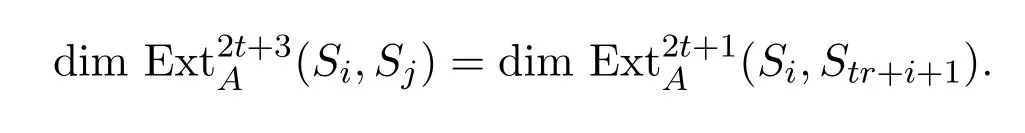
由归纳假设知

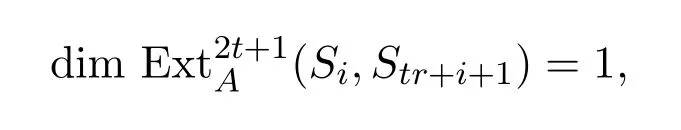
故

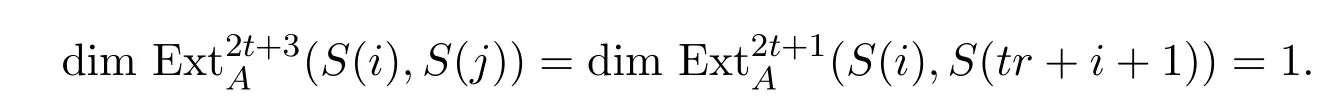
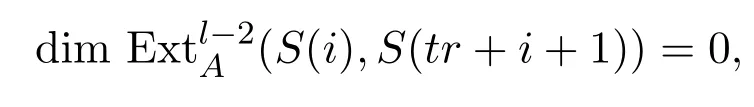
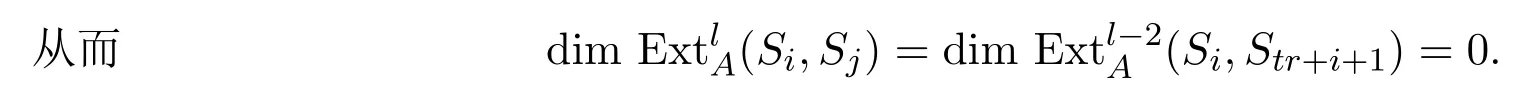
总之,由归纳可得引理对满足条件的t均成立.

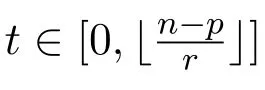
证明对t用数学归纳法.

若t=0,则j=i+p.对j∈[2,n]分以下两种情形证明引理成立.

情形 1j∈[1,r].

此时Ip+i=m(1,p+i),Ip+i−1=m(1,p+i−1),易知存在如下短正合列:

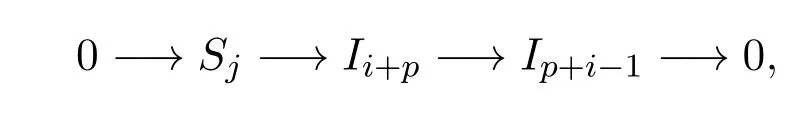
因此有

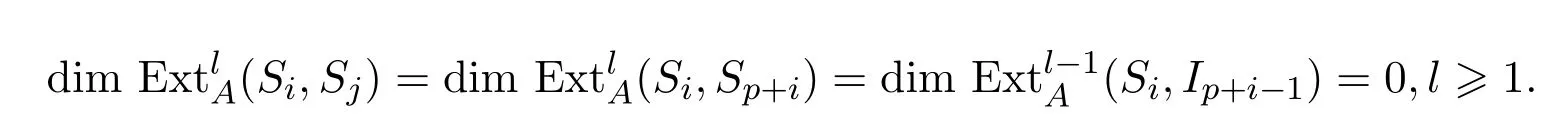
当l=0时,

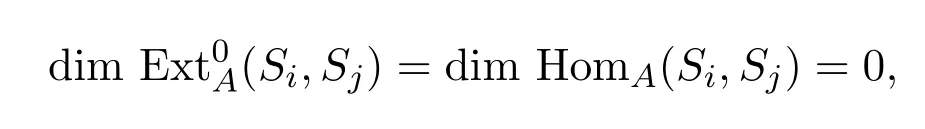
故此时引理成立.

情形 2j∈[r+1,n].

此时Ip+i=m(p+i−r+1,p+i),Ip+i−1=m(p+i−r+2,p+i−1),易知存在如下短正合列:

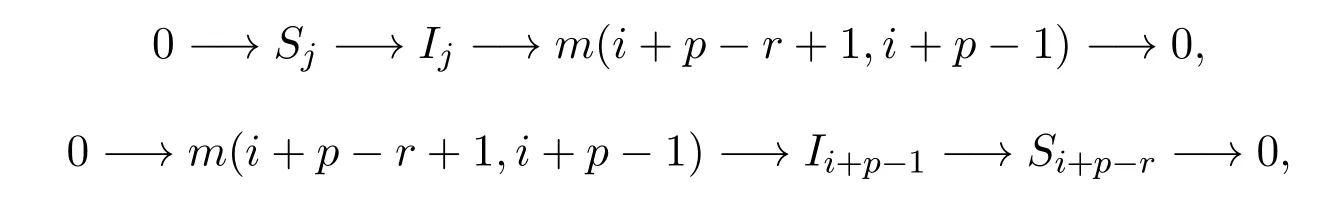
所以

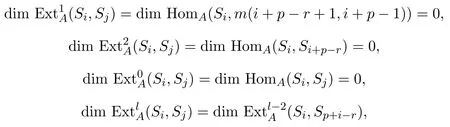
对任意的l≥3.因为r≥2,p∈[2,r−1],i−r+p＜i,从而由引理3.6知.故此时引理成立

假设j−i=tr+p时,对任意的非负整数l,.下设j−i=(t+1)r+p.易知存在如下短正合列

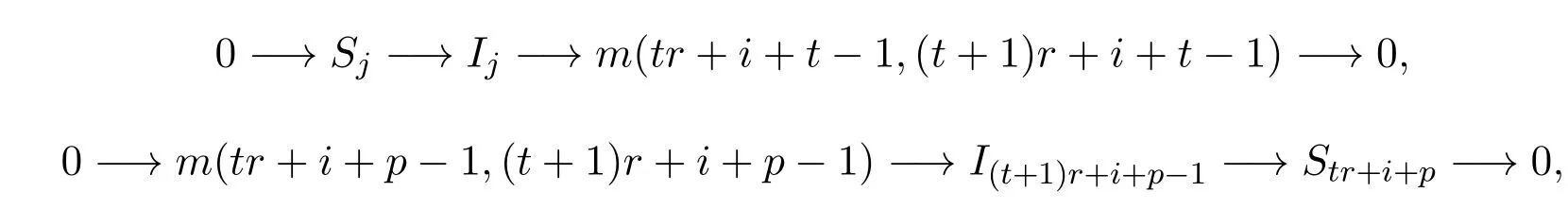
得到如下正合列 0−→Sj−→Ij−→I(t+1)r+i+p−1−→Str+i+p−→0,所以

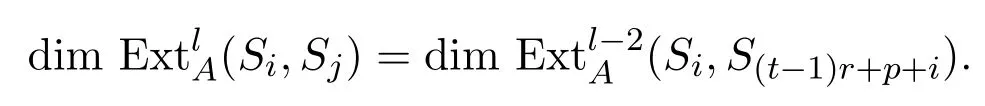
由归纳假设知

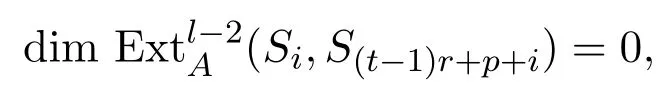
且对任意的l−2≥0,有,所以

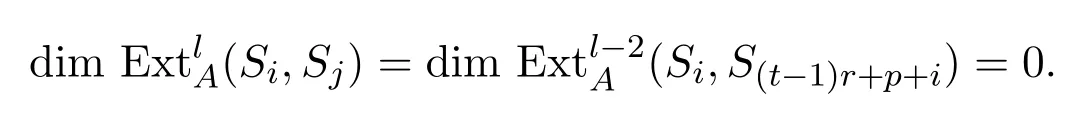
对l≥2,有

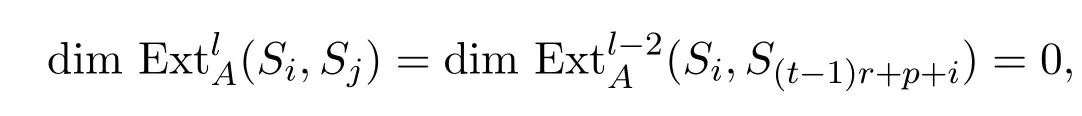
由前可知当l=0,1时,有.故引理成立.

总之,由归纳可得引理对满足条件的t均成立.

4 定理的证明

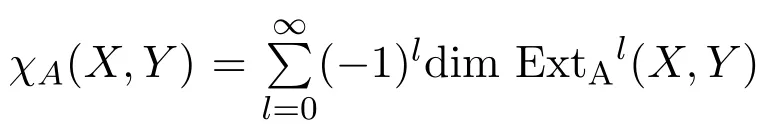
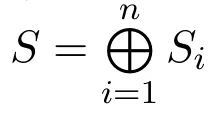
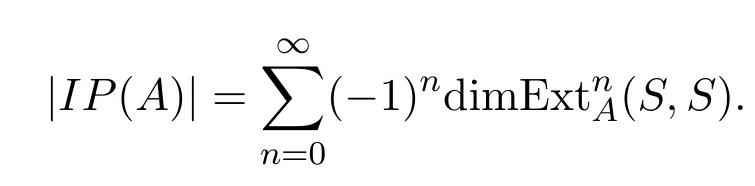
定理 4.2设k为代数封闭域,A=kQ/I为无圈型Nakayama代数,其中Q为含n个顶点的无圈箭图,I=(kQ+)r,r≥2,令n=ar+x,则代数A的量

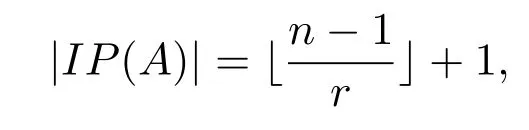
即当x=0时,|IP(A)|=a;当x/=0时,|IP(A)|=a+1.

证明对i,j∈[1,n],若i＞j,由引理3.6知,对任意的非负整数l,有,

则

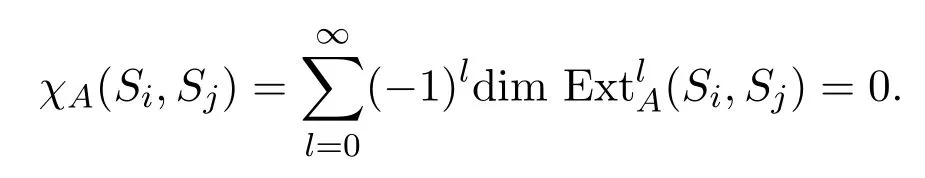
若i＜j,可令j−i=tr+m,m∈[0,r−1].若j−i=tr时,由引理3.7知,

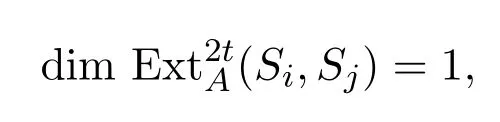
且对任意l/=2t,,则

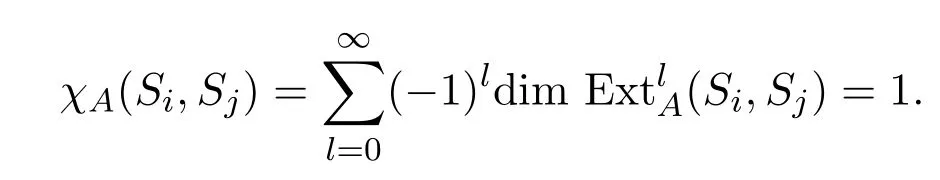
若j−i=tr+1时,由引理 3.8知,,且对任意l/=2t+1,,则

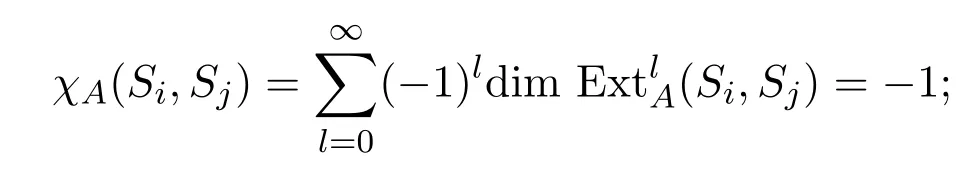
若j−i=tr+p,p∈[2,r−1]时,由引理3.9知,,则

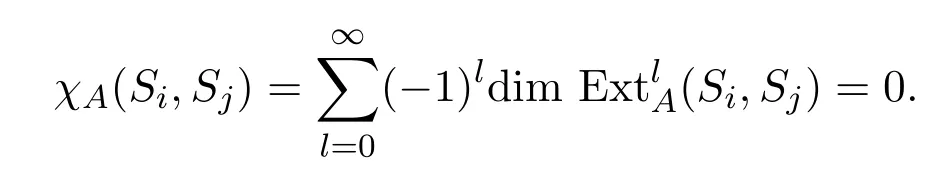
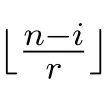
因此对给定的i∈[1,n−1],

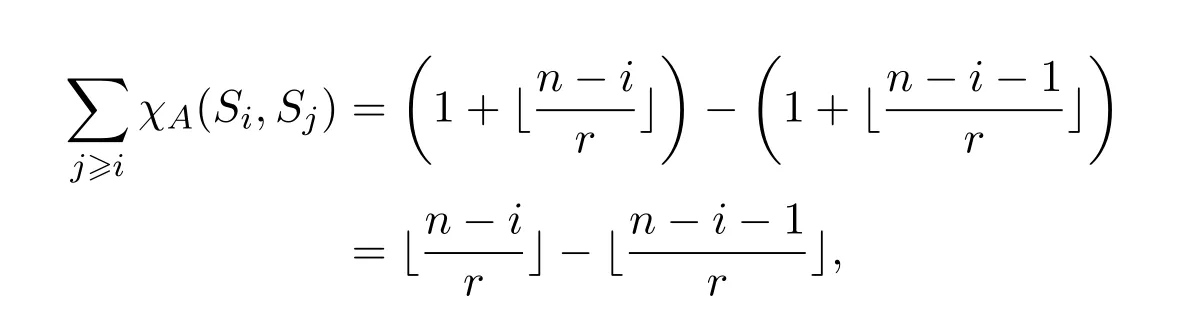
从而

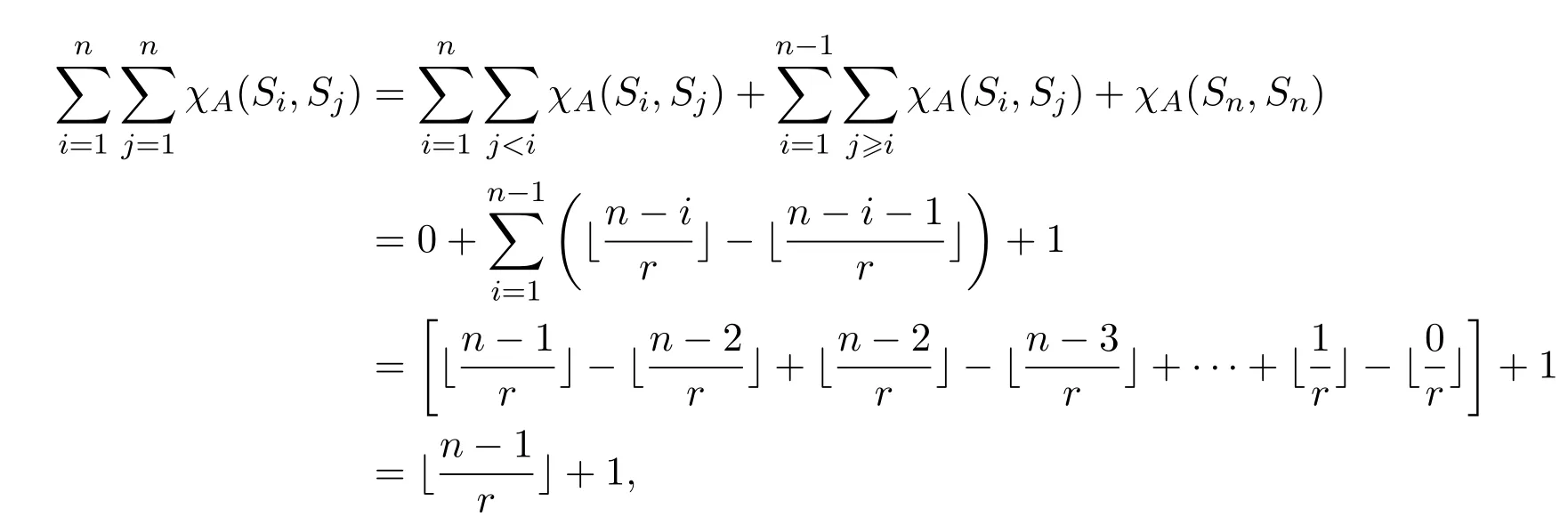
故由引理4.1,

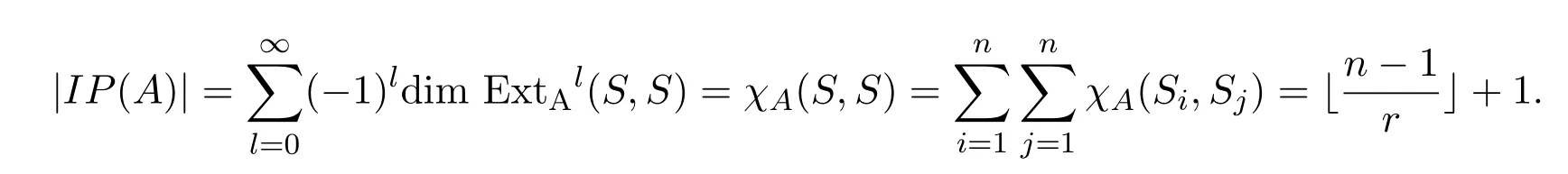
[1]Leinster T.The magnitude of metric spaces[J].Document Math.,2013,18:857-905.

[2]Chuang J,King A,Leinster T.On the magnitude of a fi nite dimensional algebra[J].Theory Appli.Categories,2016,31:63-72.

[3]Meckes M W.Magnitude,diversity,capacities,and dimensions of metric spaces[J].Potential Anal.,2015,42:549-572.

[4]Crawley-Boevey W.Lectures on representations of quivers[J].Commentarii Mathematici Helvetici,1992,69(1):137-141.

[5]Assem I,Simson D,Skowronski A.Elements of the Representation Theory of Associative Algebras[M].New York:Cambridge University Press,2006.

[6]佟文廷.同调代数引论[M].北京:高等教育出版社,1996.

Magnitudes of a class of Nakayama algebras with acyclic quivers

Shen Ping,Chen Zhengxin
(College of Mathematics and Informatics,Fujian Normal University,Fuzhou 350117,China)

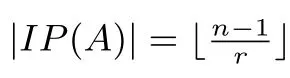
Nakayama algebras,homomorphic method,magnitudes of algebras

2010 MSC:90C25

O178

A

1008-5513(2017)06-0623-11

10.3969/j.issn.1008-5513.2017.06.008

2017-09-01.

国家自然科学基金(11571360);福建省教育厅高校青年重点项目(JZ160427);福建省自然科学基金项目(2016J01006).

沈萍(1992-),硕士生,研究方向：代数表示论.