协变量维数趋于无穷的复合次序模型的GEE估计的渐近性质

刘永睿,尹长明,孙晗

(广西大学数学与信息科学学院,广西 南宁 530000)

协变量维数趋于无穷的复合次序模型的GEE估计的渐近性质

刘永睿,尹长明,孙晗

(广西大学数学与信息科学学院,广西 南宁 530000)

研究了协变量维数趋于无穷的复合次序Logisti回归纵向数据模型.首先在响应变量为k个有序“状态”之一时,给出了该模型下的广义估计方程,然后给出了该广义估计方程估计的渐近存在性,相合性以及渐近正态性定理,并在较弱的条件下给出了定理的证明过程,证明了该模型的可用性以及结果的稳定性,推广了文献中的相关结果.

属性数据;高维协变量;相合性;渐近正态性

1 引言

复合次序模型是多维广义线性模型中的一种,主要研究目标变量Y取k个有序“状态”,而这k个状态又被自然分成几个小类,每个小类性质接近.建模时,首先对不同类之间进行建模,然后对每个小类用不同的参数进行建模.如药物对病人治疗效果可分为三类:改善,没有变化,恶化.而第一类改善又分为有很大改善,有改善,第三类恶化又分为一般恶化,严重恶化[1].广义估计方程 (GEE)是Liang和 Zeger[2]于 1986年提出,用于分析纵向数据 (longitudinal data)或集团数据(cluster data)的一种模型,是广义线性模型的推广.文献[3]详细讨论了纵向数据下的GMM方法以及GEE,并针对纵向数据下广义估计方程给出了两种经验似然方法,得到了参数的极大经验似然估计.文献[4]讨论了Logit模型的参数估计.本文运用了Logit模型的基本思想,讨论了协变量维数趋于无穷的复合次序模型的广义估计方程的相关性质,解决了一些高维数据的统计推断问题,并将广义估计方程的应用领域扩展至目标变量取个有序“状态”之一的属性数据,推广了文献[5]中的相关结果.

2 模型介绍

设对第i个个体的第j次观测,得到q×1维响应变量Yij,pn×q维协变量Zij,i=1,···,n,j=1,···,m,q=k−1.设来自不同个体的观测值相互独立,来自相同个体观测值则是相关的,但相关系数未知.令Yij=(Yij1,···,Yijq)T的期望

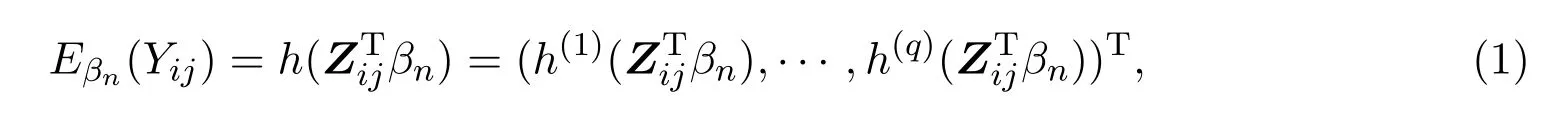
其中h是联系函数,βn是pn×1维未知回归参数(pn可以趋于无穷),βn0为参数的真值,T表示转置.记

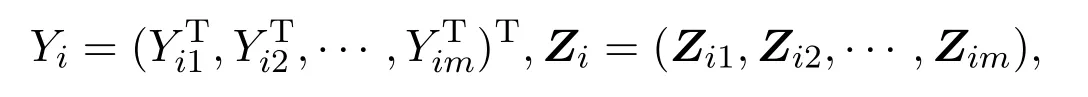
Yi的期望记为:

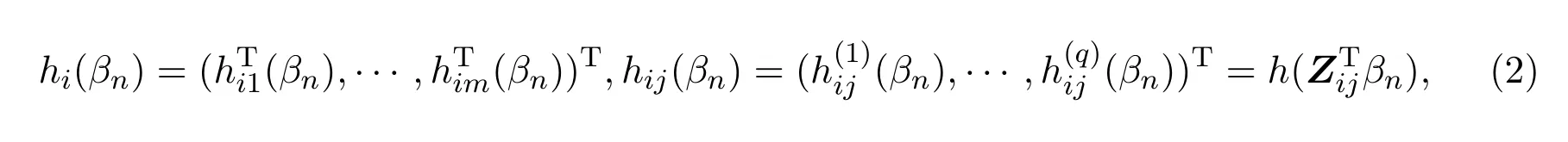
方差记为:

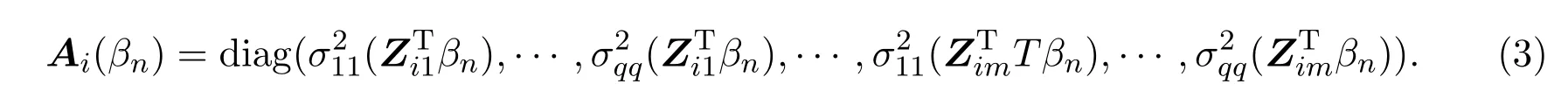
当Yij服从0,1分布(观察次数是1的二项分布),期望

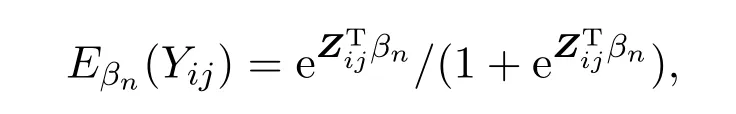
即

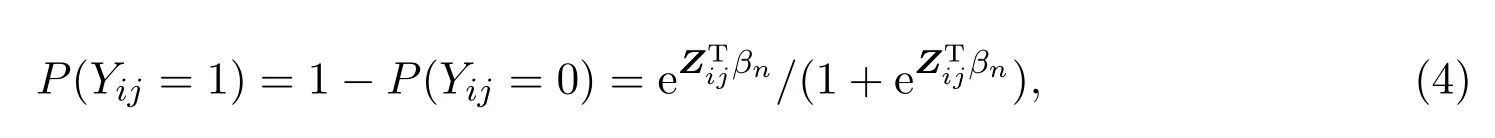
就得到经典的Logit模型.

若Yij服从五项分布(观测次数是1),即q=4,期望

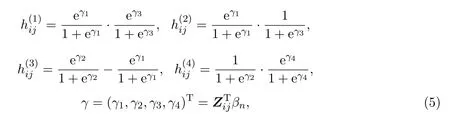
即

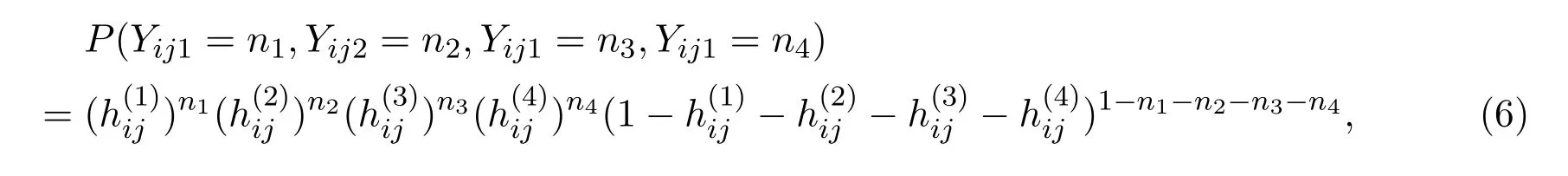
其中n1,n2,n3,n4,n1+n2+n3+n4=0,1,就得到复合次序Logit模型[1].

文献[5]在一定条件下证明了经典Logit广义估计方程:

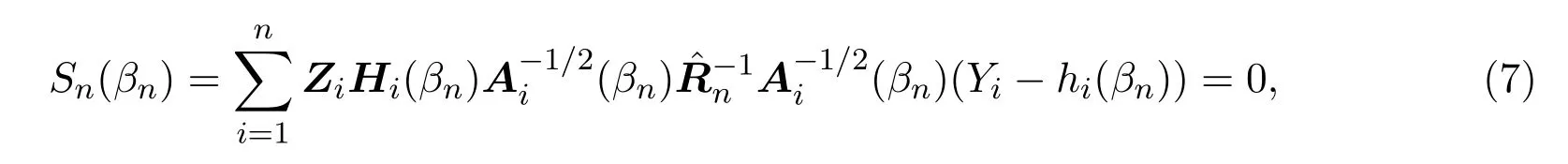
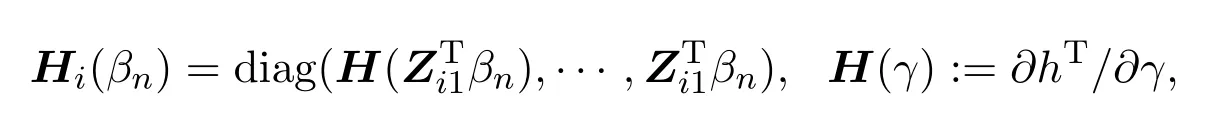
3 主要结果

为了后面定理叙述简单，引入以下假设条件:

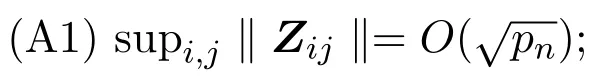
(A2)未知参数βn属于紧子集B⊆Rpn,真正参数值βn0是集合B的内点,并且存在正常数c,

使得λmin(Ai(βn0))≥c,其中λmin,λmax分别表示矩阵的最小,最大特征值;

(A3)存在两个正的常数c1,c2,满足:

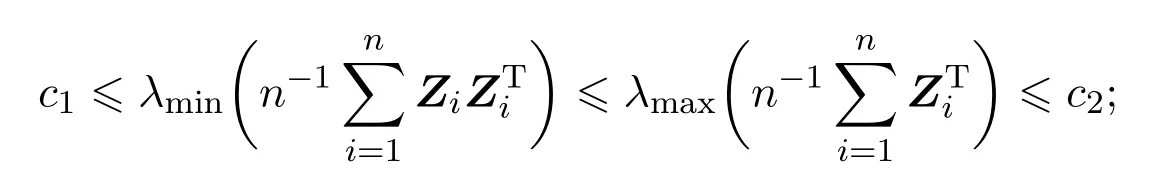
(A4)

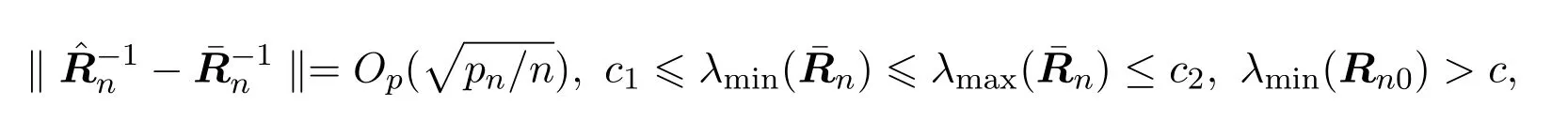
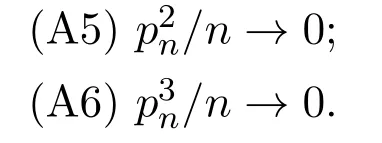
定理3.1对复合次序模型,假设(A1)-(A5)成立,则方程Sn(βn)=0存在一个根ˆβn,且满足如下条件:

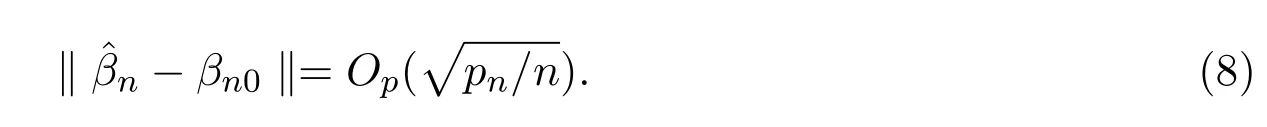
进一步假设 (A6)成立，则∀αn∈Rpn,‖αn‖=1,有

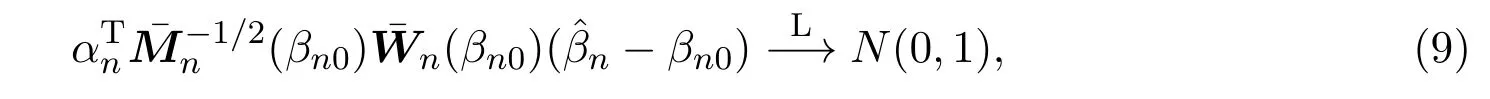
其中

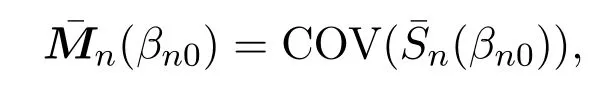
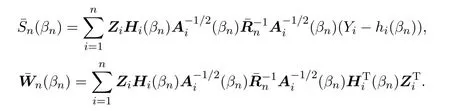
注3.1对经典Logit模型,

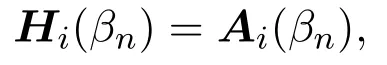
方程(7)就简化为文献[5]中方程(3.1).

注 3.2该定理的假设条件与文献[5]一样,参看文献[5].

4 定理3.1的证明

定理的证明需要用到以下引理:

引理4.1设G是Rn中的有界开集,记G的闭包和边界分别是,∂G.若函数是连续的,并且对某个x0∈G和所有的x∈∂G有(x−x0)TF(x)≤0,则F(x)=0有一个根在中.参见文献[6].

下面5个引理的证明分别与文献[3]引理3.1,引理3.3,引理3.4,引理3.5,引理3.7类似,在此省略.

引理 4.2若假设条件(A1)-(A5)成立,则

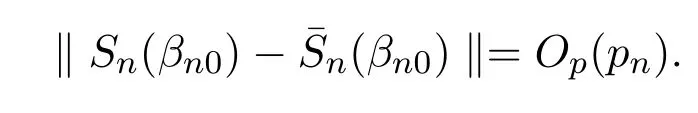
引理 4.3若假设条件(A1)-(A5)成立,则∀Δ＞0,an,bn∈Rpn,有

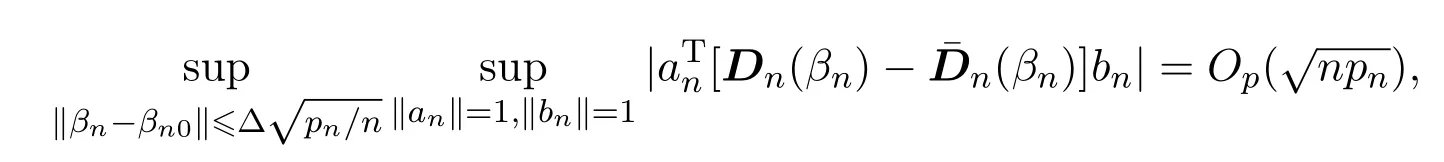
其中

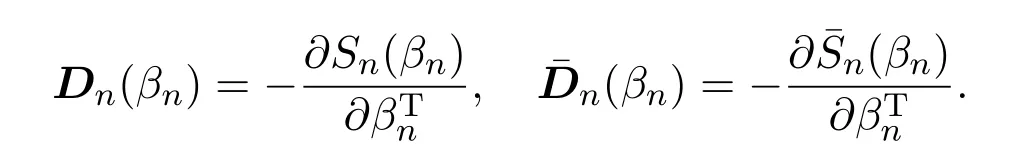
引理 4.4若假设条件(A1)-(A5)成立,则∀Δ＞0,an,bn∈Rpn,有

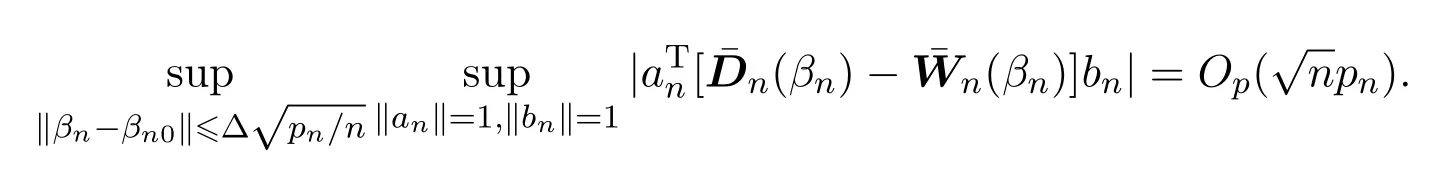
引理 4.5若假设条件(A1)-(A5)成立,则∀Δ＞0,an,bn∈Rpn,有

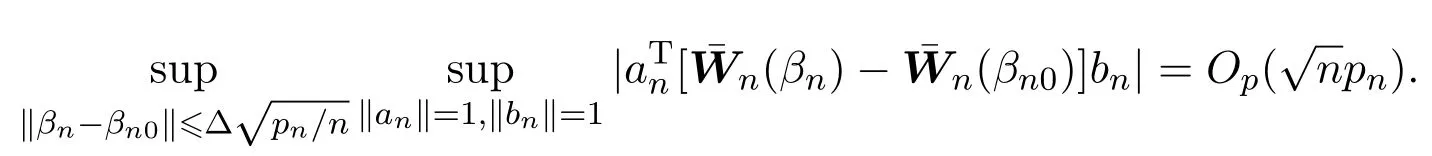
引理 4.6若假设条件(A1)-(A4)及pn/n→0成立,则∀α∈Rpn,‖αn‖=1有

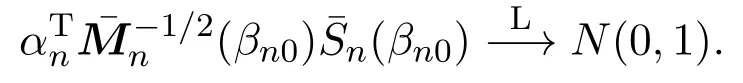
定理 3.1的证明根据引理4.1,证明方程Sn(βn)=0根的存在性且(8)成立,只需证明∀ε＞0,存在一个Δ＞0,对足够大的n有如下式子成立:

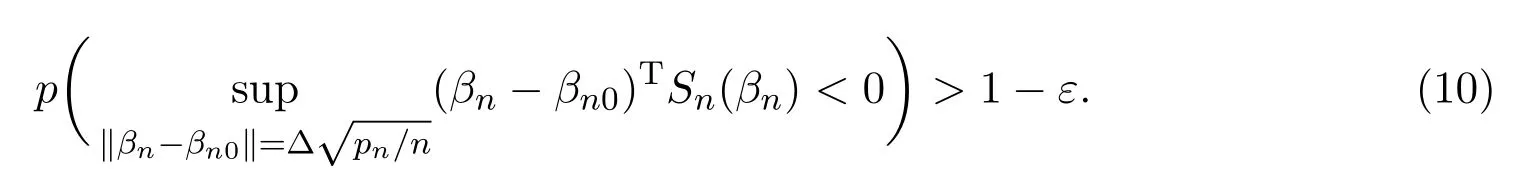
由微分中值定理,有

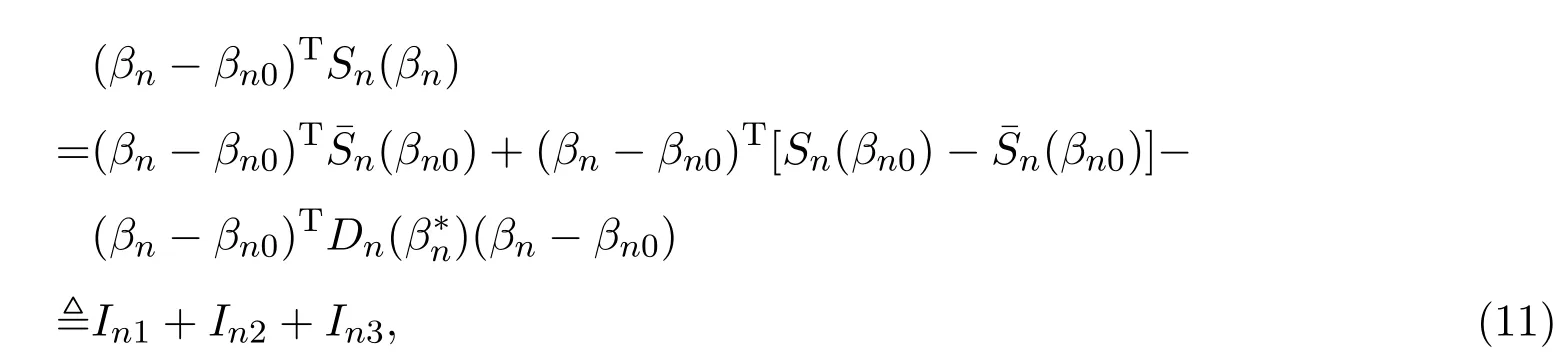
由Hi(βn0),Yi的定义知其有界,由假设(A2)和(A4)分别知和都有界,再由 (A3),有

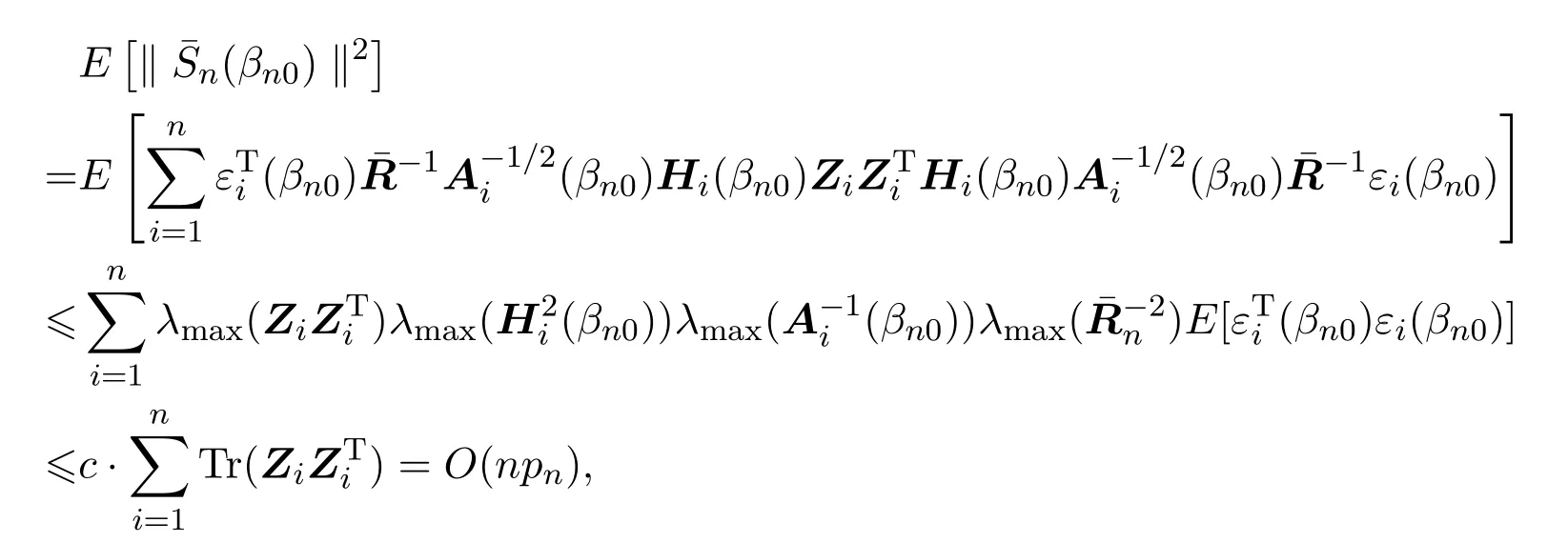
其中,εi(βn)=Yi−hi(βn). 所以

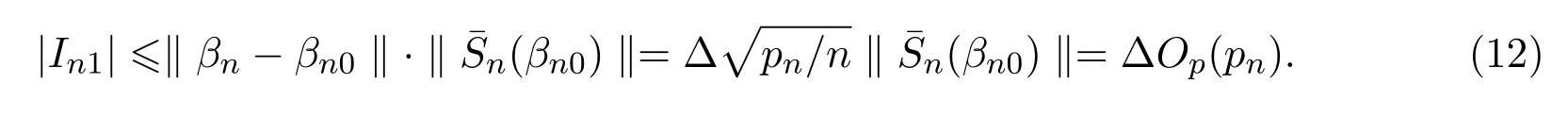
由引理4.2及假设(A5)可得：

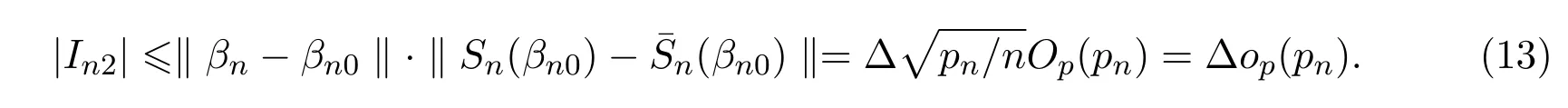
对于In3有,

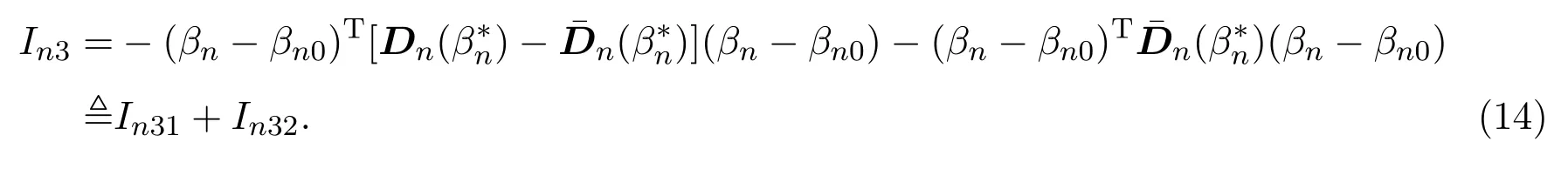
由引理4.3和假设(A5)可得,

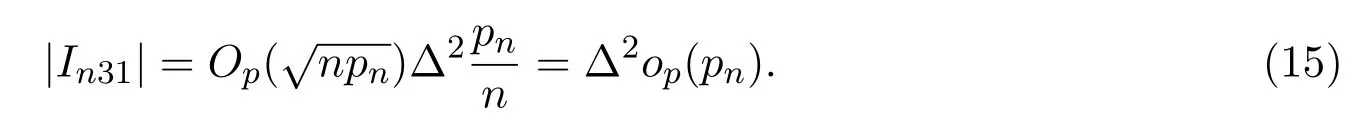
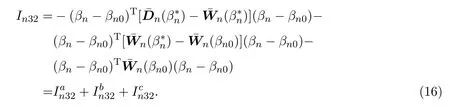
由引理4.4和引理4.5及假设(A5)可得,

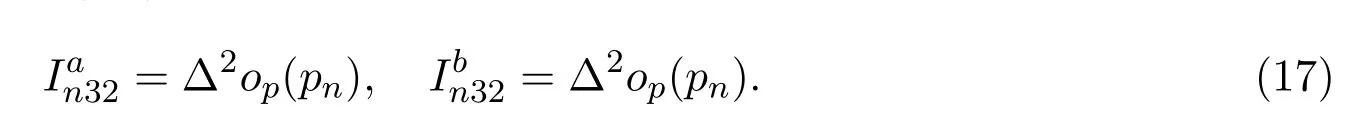
而由假设(A2),(A3)和(A4)可得,

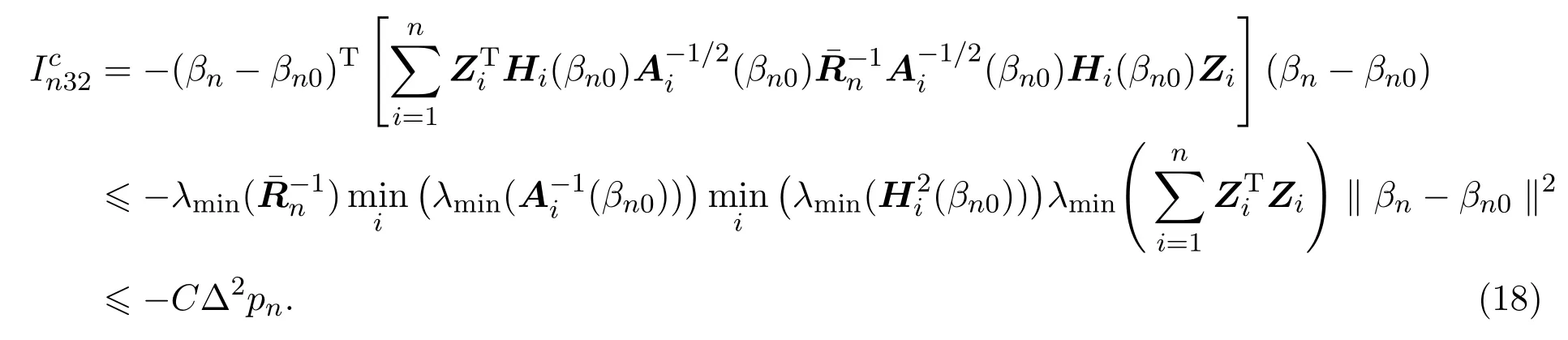
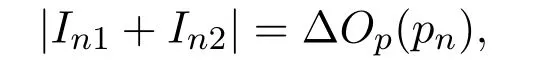
可见当Δ足够大时,(10),(8)成立.

下面证(9)式成立.

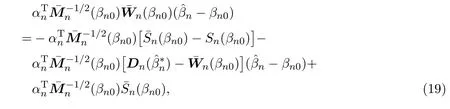
由假设条件(A4)和(A2)可得,

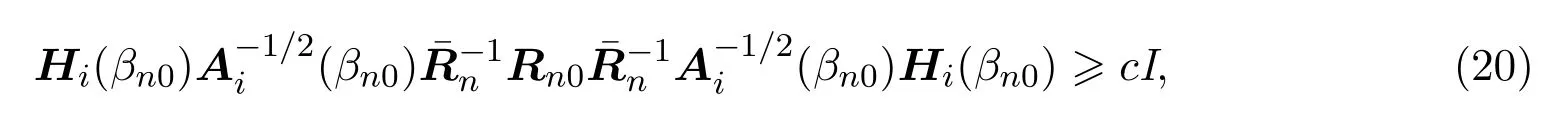
再由假设条件(A3),引理4.2和(A5)可得,

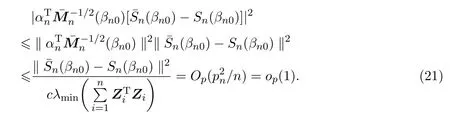
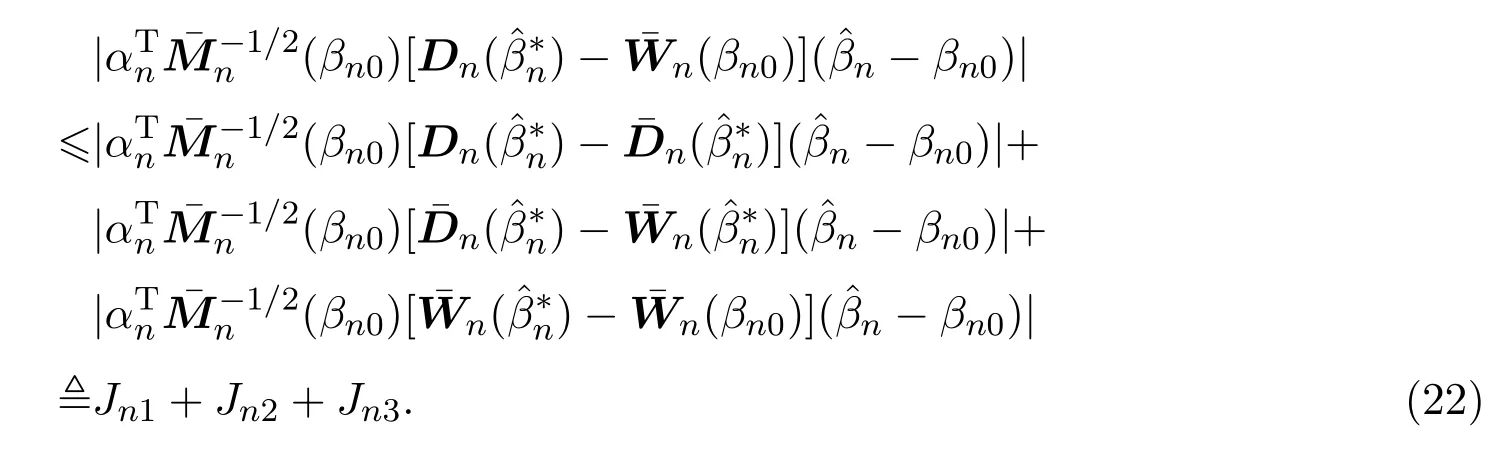
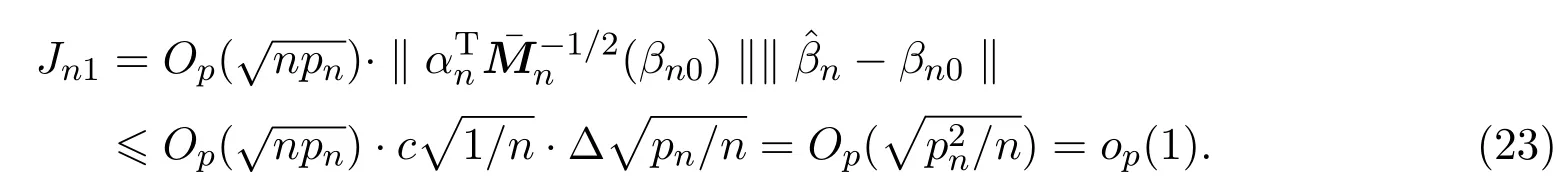
同理,运用(8),引理4.4,引理 4.5,假设 (A3),(A6)可得,

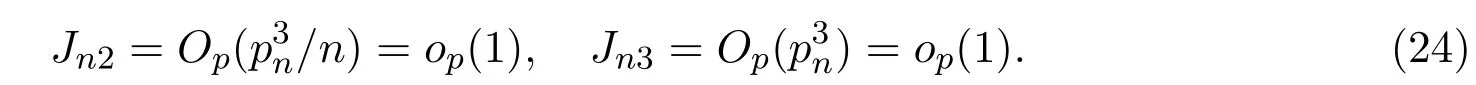
由(19),(21)-(24)式,引理4.6和Slutsky定理可知,(9)式成立.

[1]Fahrmeir L,Tutz G.Multivariate Statistcal Modelling Based on Generalized Linear Models Equation Concerning[M].New York:Springer-Verlag,1994.

[2]Liang K Y,Zeger S L.Longitudinal data analysis using generalized linear models[J].Biometrika,1986,73:13-22.

[3]赵目,陈柏成,周勇.纵向数据下广义估计方程估计[J].数学学报:中文版,2012,55(1):1-16.

[4]孙海云.Logit模型参数估计方法的研究[D].浙江:浙江大学,2016.

[5]Wang L.GEE analysis of clustered binary data with diverging number of covariates[J].Ann.Statist.,2011,39:389-417.

[6]Ortega J M,Rheinboldt W C.Iterative Solution of Nonlinear Equations in Several Variables[M].San Diego:Academic Press,1970.

Asymptotic properties of compound order logit model with diverging number of covariates

Liu Yongrui,Yin Changming,Sun Han,
(Guangxi University,Academy of Mathematics and Information Sciences,Nanning 530000,China)

In this paper,we study the compound ordinal logit regression model with diverging number of covariates.First,we propose the GEE of this modle on condation that the response variable denote one of status.Then we bring up the asymptotic existence,consistency and asymptotic normality theorem and under some mild conditons,we provide the evidentiary process.The practicability and stabilization of this model is proved.We extend the relevant results in the literature.

categorical data,high-dimensional covariates,consistency,asymptotic normality

2010 MSC:62J12,62F12

O212.1

A

1008-5513(2017)06-0578-07

10.3969/j.issn.1008-5513.2017.06.004

2017-10-20.

国家自然科学基金(11061002);广西自然科学基金(2015GXNSFAA139006).

刘永睿(1990-),硕士生,研究方向：统计学.