树上非齐次马氏链转移矩阵的若干极限性质

金少华,于凯丽,任双双,李小雪

(河北工业大学理学院,天津 300401)

树上非齐次马氏链转移矩阵的若干极限性质

金少华,于凯丽,任双双,李小雪

(河北工业大学理学院,天津 300401)

树模型近年来已引起物理学、概率论及信息论界的广泛兴趣.树指标随机过程已成为发展起来的概率论的研究方向.在概率论的发展过程中,对强极限定理的研究一直占重要地位,强极限定理也一直是国际概率论界研究的中心课题之一.本文通过引入样本散度的概念,通过构造适当的非负鞅,将Doob收敛定理应用于几乎处处收敛的研究,给出了非齐次树上m重可列非齐次马氏链转移矩阵的若干极限性质.

非齐次树；鞅；马氏链；强极限定理

1 引言

树模型近年来引起了物理学、概率论、信息论及金融学界的广泛兴趣,树指标随机过程已成为近年来发展起来的概率论的研究方向之一.强偏差定理（又叫小偏差定理）是用不等式表示的一类强极限定理.强极限定理一直是国际概率论界研究的中心课题之一.关于树上马尔科夫链场的早期研究见文献[1]及其所引文献.文献[2]研究给出了N值随机变量序列的马尔科夫逼近和一类强偏差定理.文献[3]研究给出了齐次树上随机场泛函的若干强偏差定理.文献[4]研究给出了N值随机变量序列对于m阶齐次马氏链的若干强偏差定理.文献[5]研究给出了树指标随机过程的若干强偏差定理.上述文献研究的状态空间均是有限集,本文将其推广到可列无限集.本文通过引入样本散度的概念,通过构造适当的非负鞅,将Doob鞅收敛定理应用于几乎处处收敛的研究,研究给出了非齐次树上m重可列非齐次马氏链转移矩阵的若干极限性质.

2 定义

设设T是一个具有根顶点O的无限树,{Nn,n≥1}是一正整数集,如果第n(n≥0)层上的每个顶点均与第n+1层上的Nn+1个顶点相邻,则称T为广义Bethe树或广义Cayley树.特别地,若对非负整数集N,用模m的同余关系对其分类得到模m的剩余类

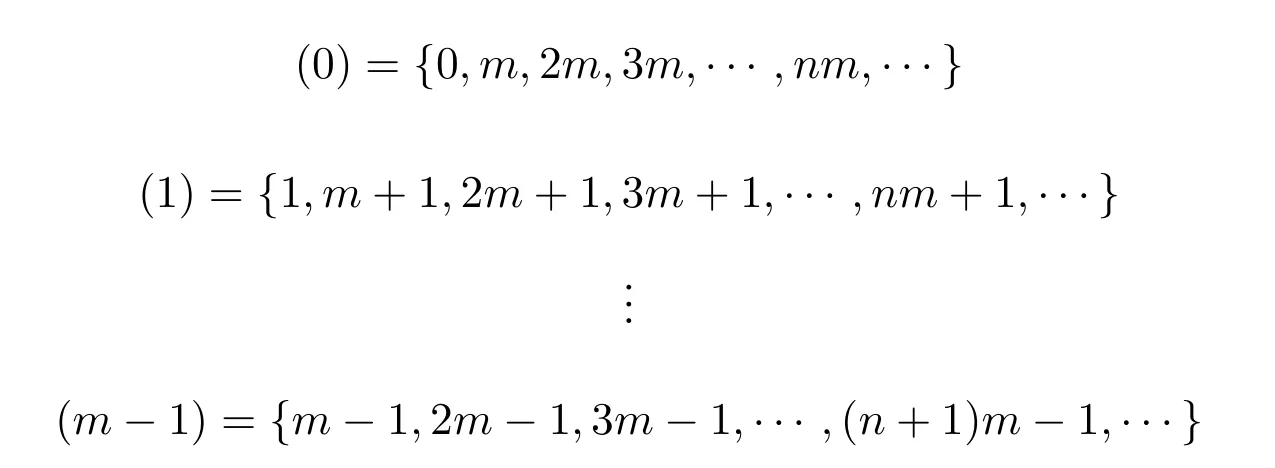
当n∈(i)时,令Nn+1=αi（αi均为正整数且不同时为1）,i=0,1,2,···,m−1,就得到了一类特殊的非齐次树Tα0,α1,··,αm−1.

以下恒以T表示树Tα0,α1,··,αm−1,以Ln表示第n(n≥0)层上所有顶点的子图,Tn表示含有从O顶点到第n层上所有顶点的子图,S(t)表示t顶点的所有子代的子图.

定义 2.1设{Xσ,σ∈T}是定义在概率空间{Ω,F,P}上并在S={s1,s2,···}上取值的随机变量族,设

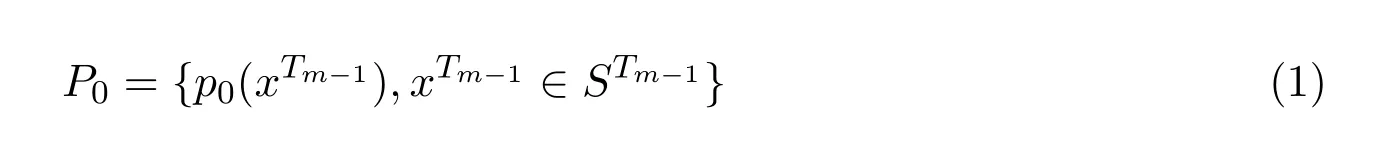
是STm−1上一概率分布,而

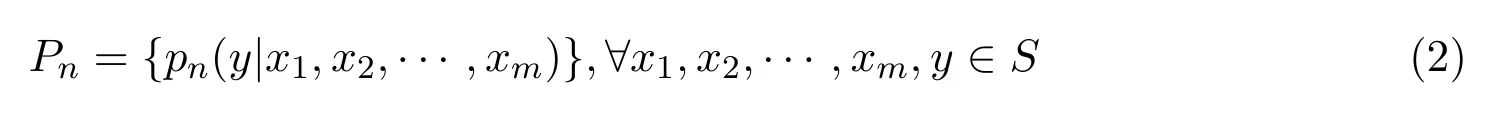
是定义在Sm+1上的随机矩阵,如果∀τ∈T,σ∈Ln,有

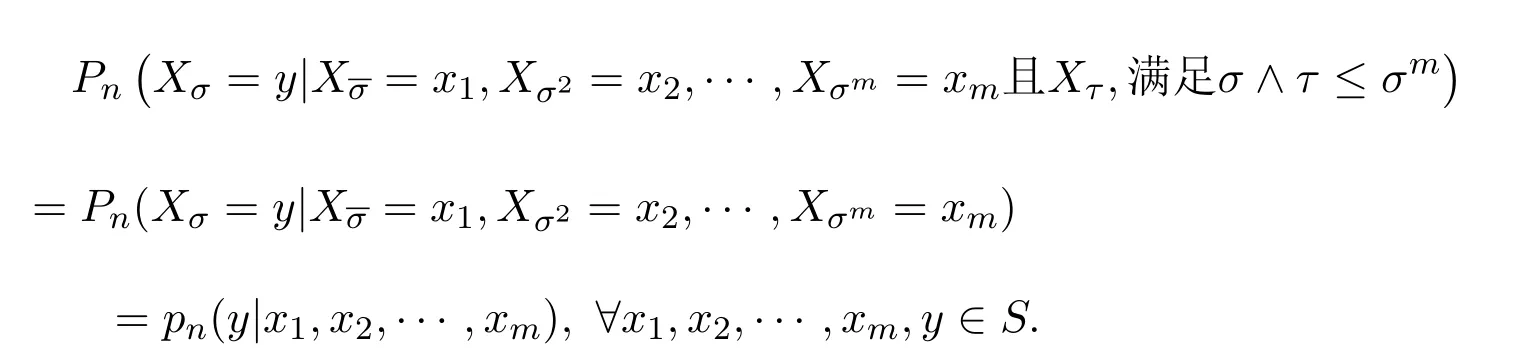
且

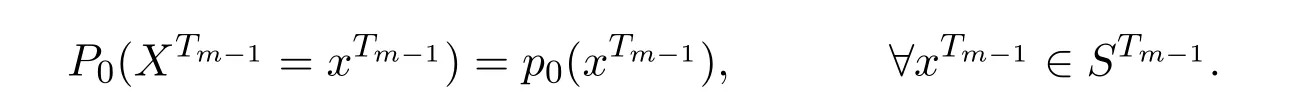
则称{Xσ,σ∈T}为具有初始分布(1)与转移矩阵列(2)的在S上取值的树T上的m重非齐次马氏链.

由上述定义知,上述树T上的m重非齐次马氏链的联合分布为:

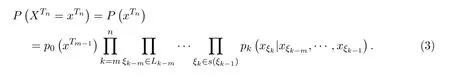
设Q是(Ω,F)上的另一概率测度,{Xσ,σ∈T}在概率测度Q:

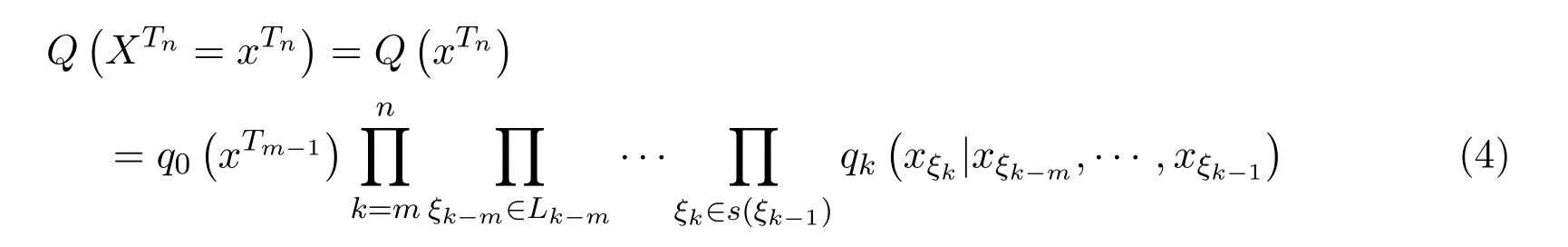
定义 2.2设P和Q均如前定义,令

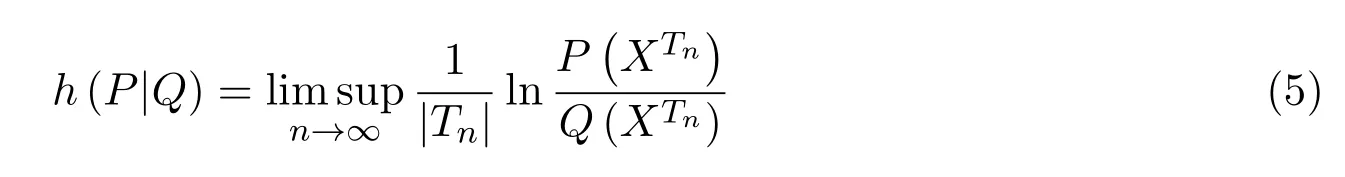
则称h(P|Q)为P相对于Q的样本散度.

3 主要结果及其证明

引理 3.1P(XTn)和Q(XTn)分别由(3)和(4)式给出,则有

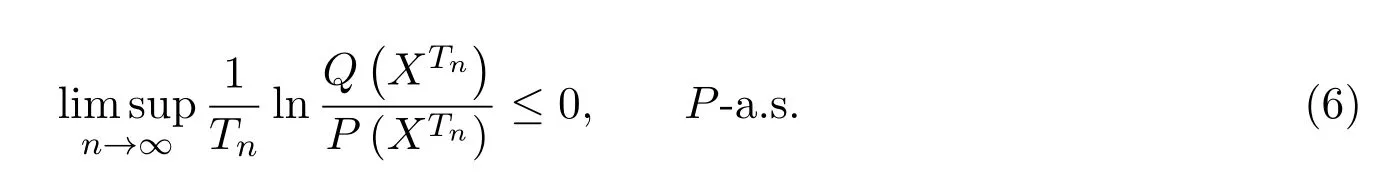
由(6)式易见

引理 3.2设{Xσ,σ∈T}是具有初始分布(1)与转移矩阵列(2)的在S上取值的树T上的m重非齐次马氏链,h(P|Q)由(5)式定义,λ为任意实数,令

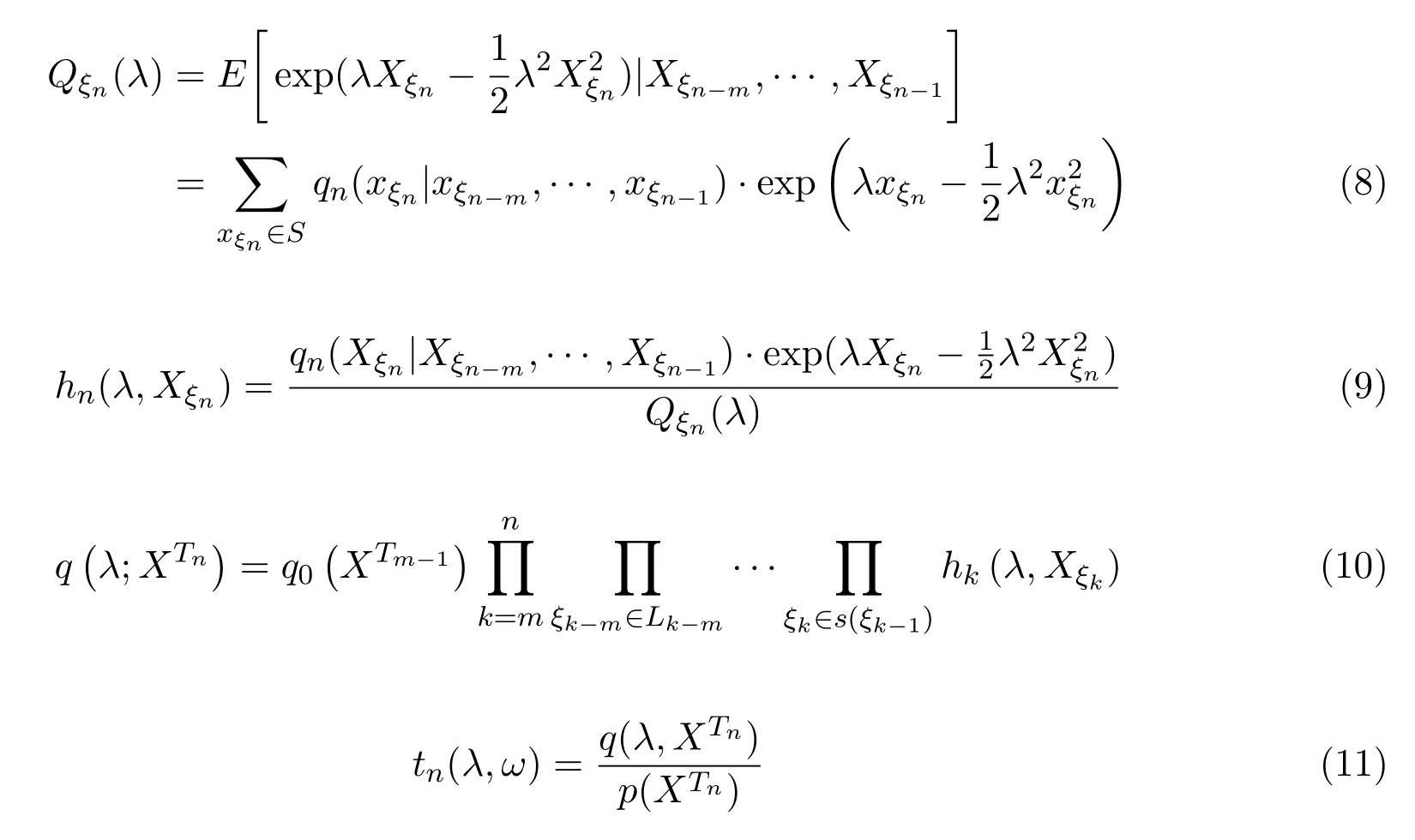
则{tn(λ,ω),σ(XTn),n≥m}在测度P下为一非负鞅.

证明由(3)式,有

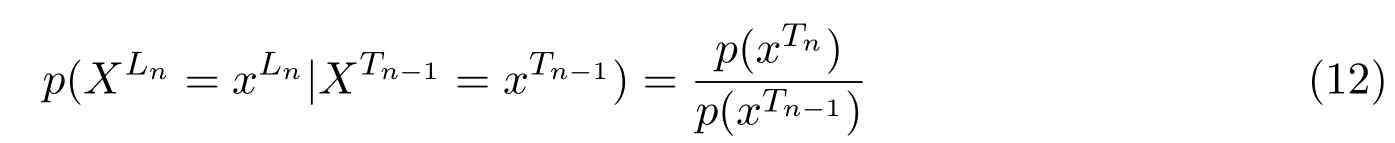
而由(9)-(11)式,有

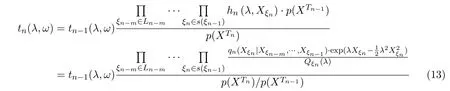
由由(13)式和条件概率的性质,有

由 (13)-(14)式,有

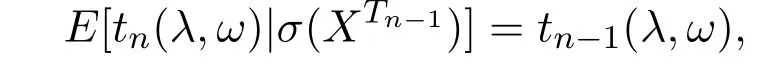
故{tn(λ,ω),σ(XTn),n≥m}在测度P下为一非负鞅.

定理 3.1设{Xσ,σ∈T}是具有初始分布(1)与转移矩阵列(2)的在S上取值的树T上的m重非齐次马氏链,且∀n＞m,有

成立.h(P|Q)由(5)式定义,令

设

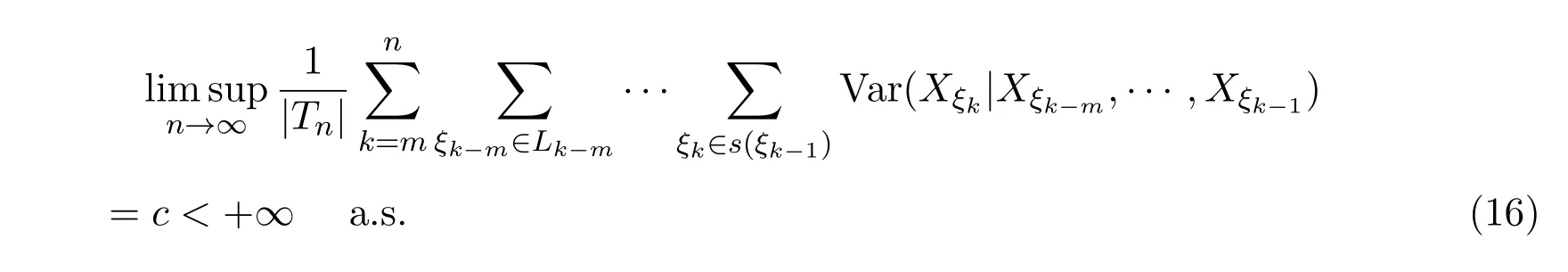
若c＞0,则有

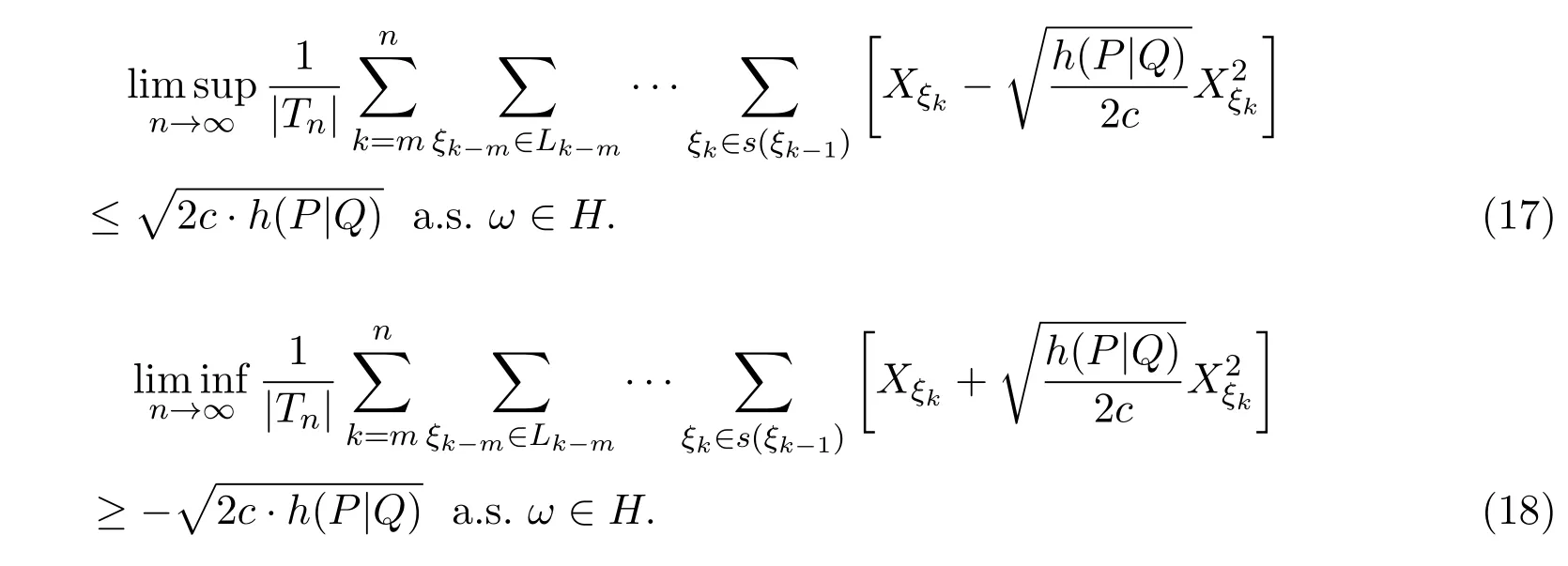
若c=0,则有

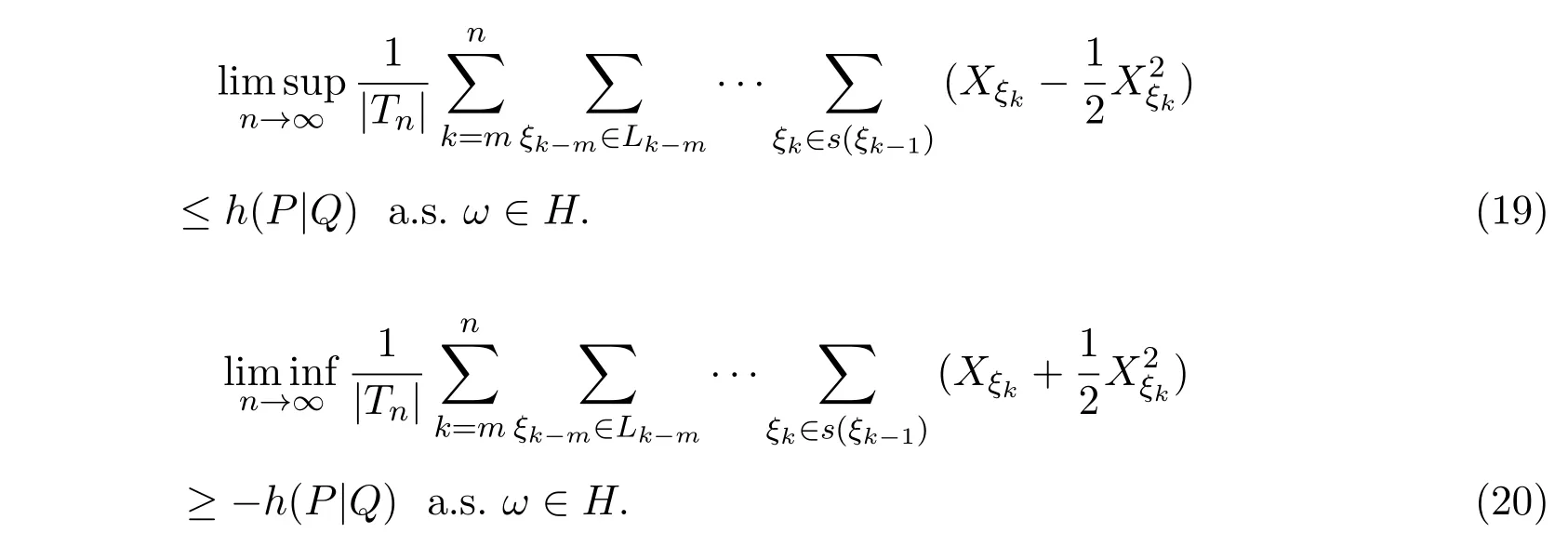
证明

textbf证明取 (Ω,F,P)为考虑的概率空间,由引理3.2知对任意常数λ,

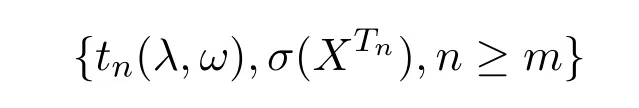
在测度P下为一非负鞅.故由Doob鞅收敛定理[6]知，存在A(λ)∈F,P(A(λ))=1,使得

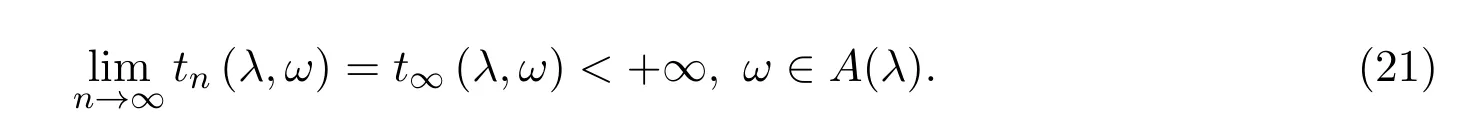
由 (21)式,有

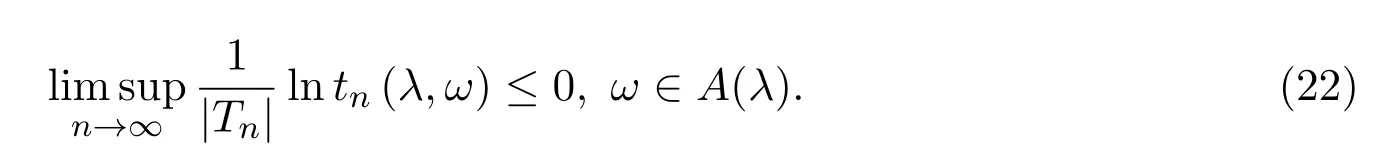
由 (8)-(11)式和 (22)式,有

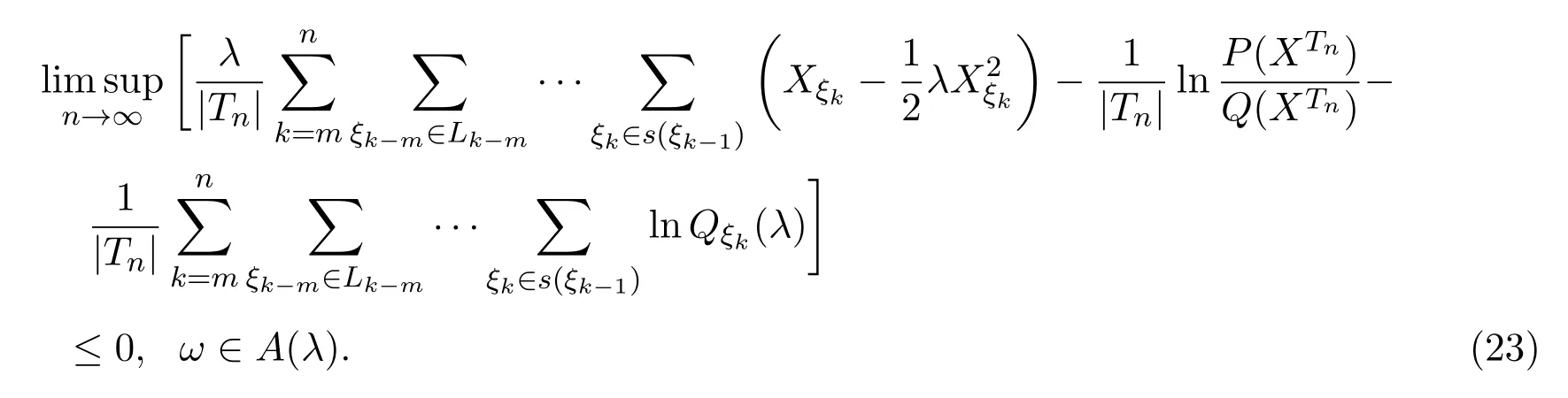
由 (23)式,有

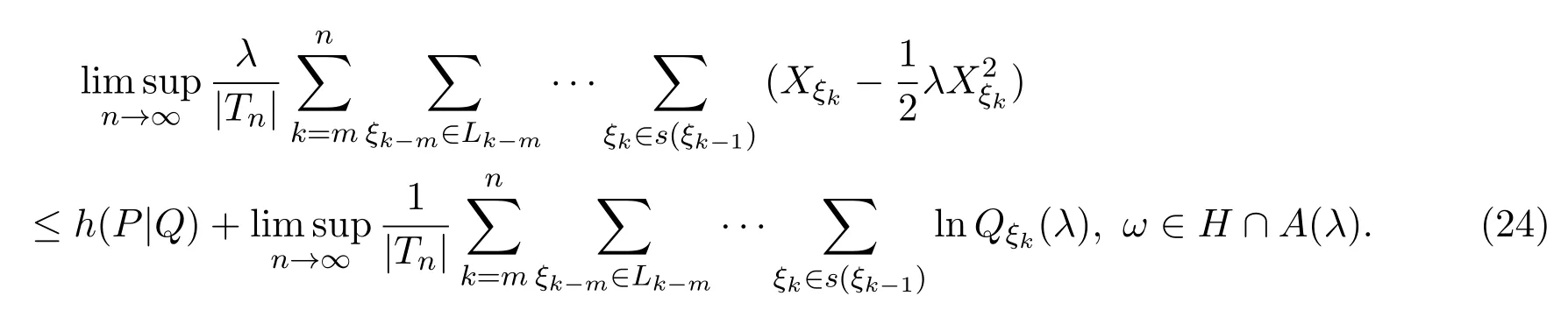
由不等式

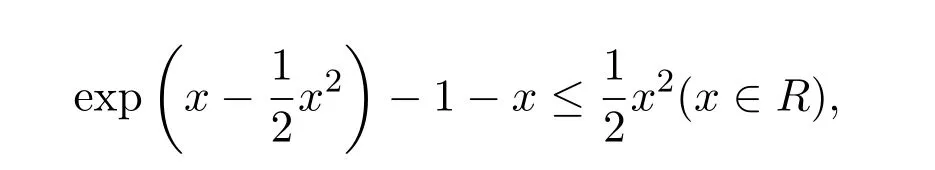
并注意到

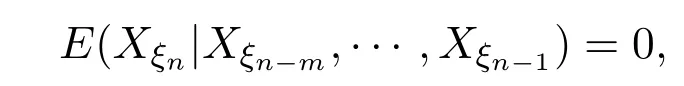
有

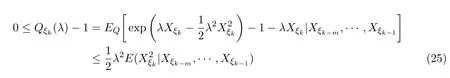
由 (16),(25)式,有

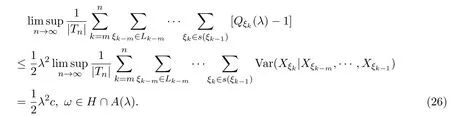
由 (26)式,有

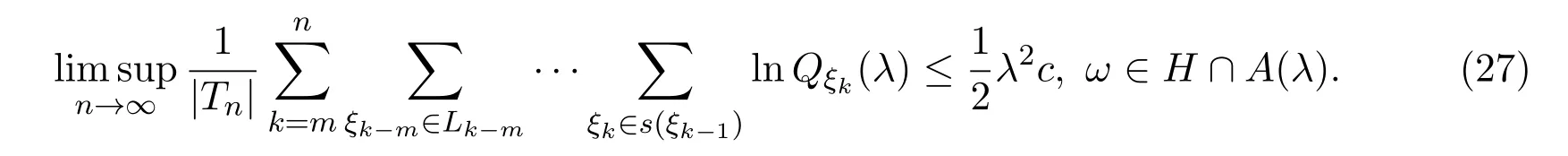
由 (24)式和 (27)式,有

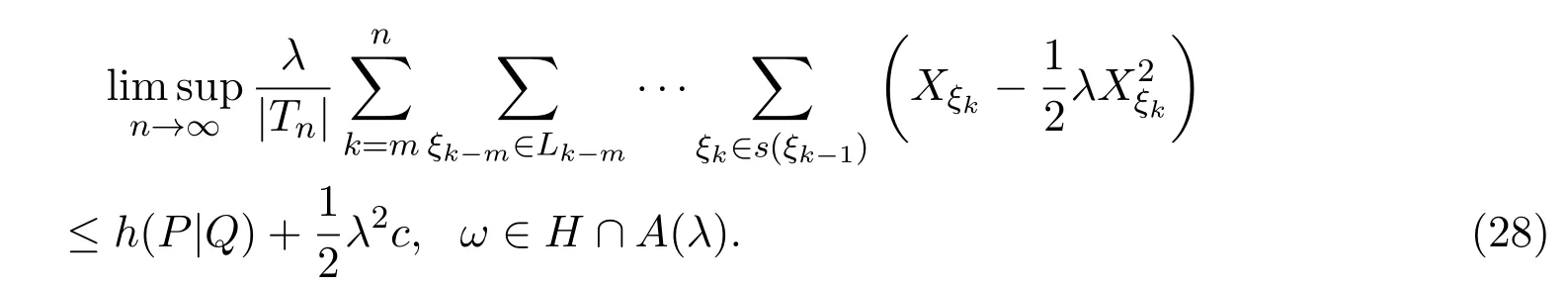
若λ ＞0，由 (28)式,有

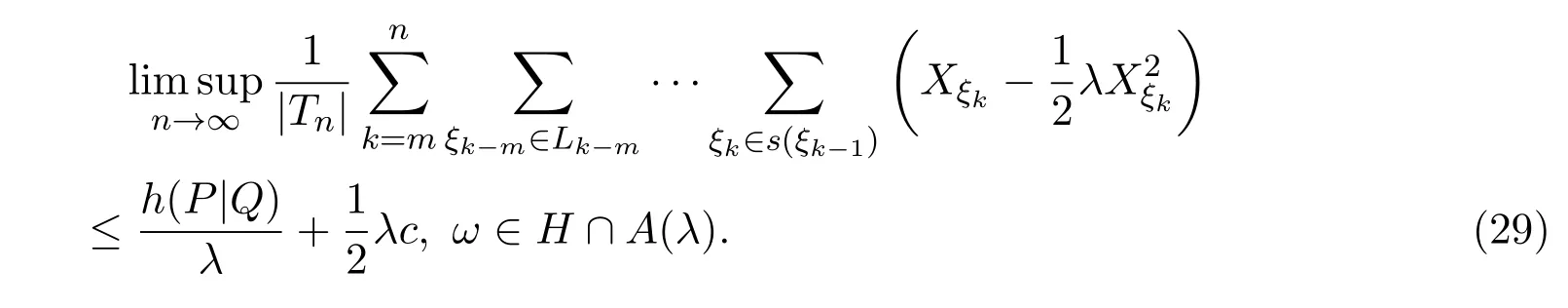
当c＞0时,因函数

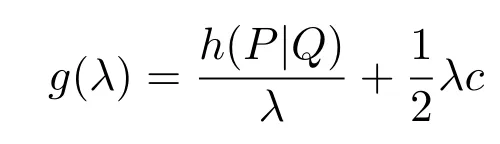
在

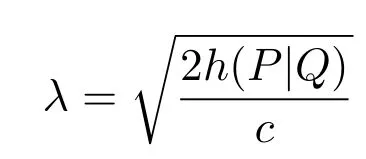
处取得最小值

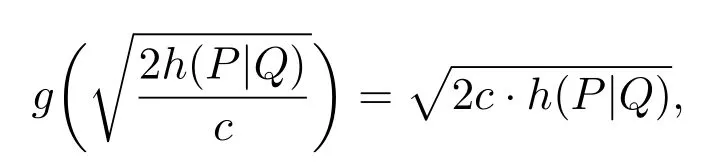
故在(29)式中令

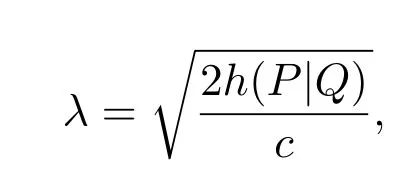
有

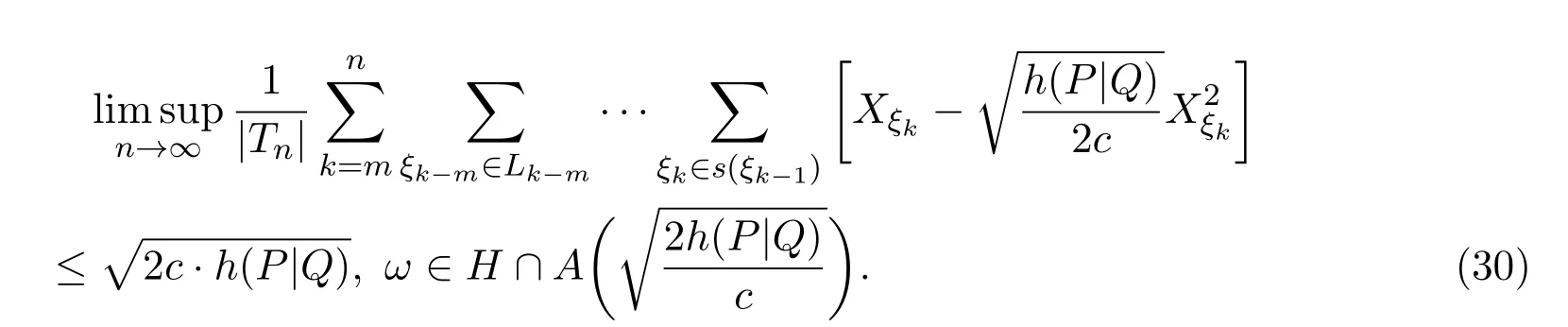
又由于

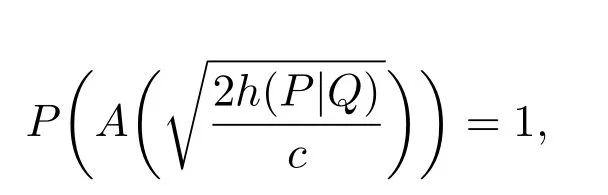
则由(30)式知(17)式成立.

若c=0，将λ=1代入 (29)式,有

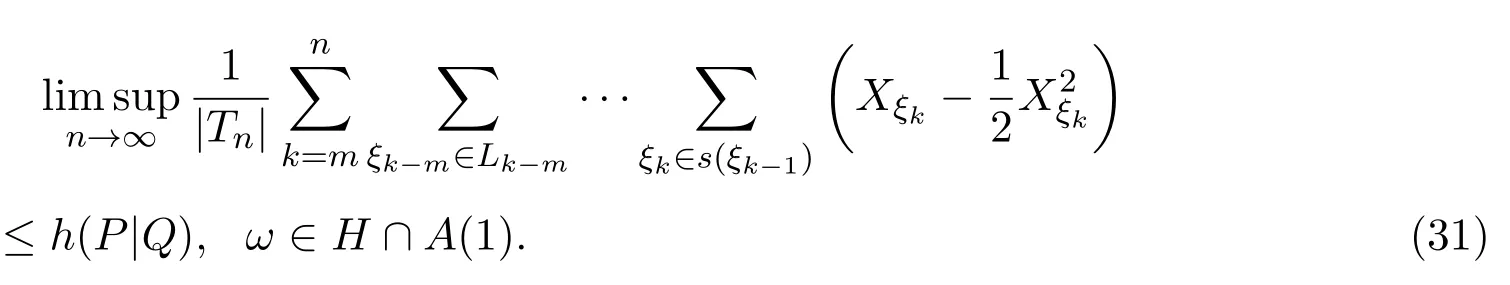
因P(A(1))=1,则由(31)式知(19)式成立.

若λ ＜0，由 (28)式,有

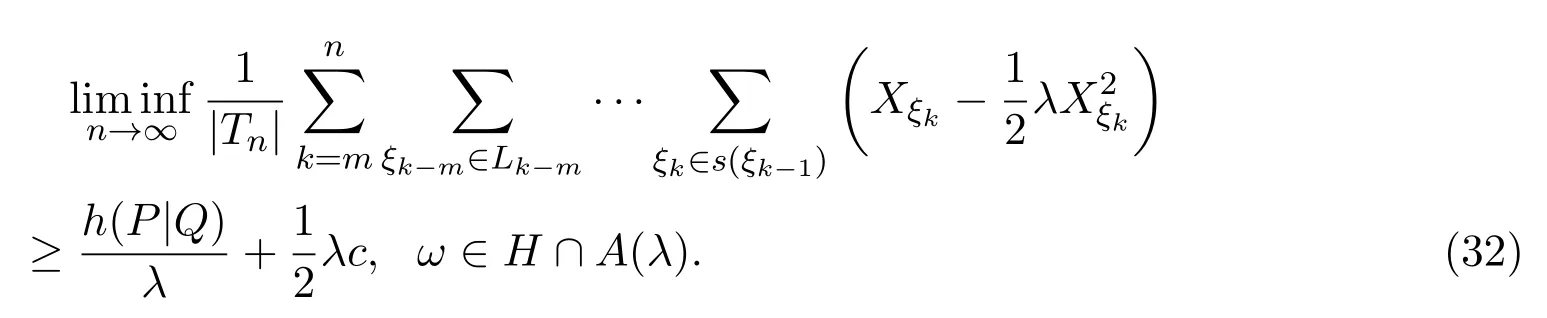
当c＞0时,因函数

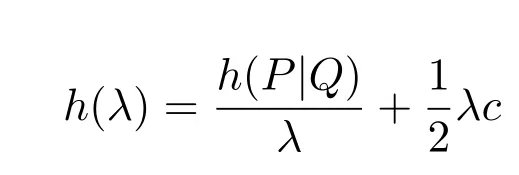
在

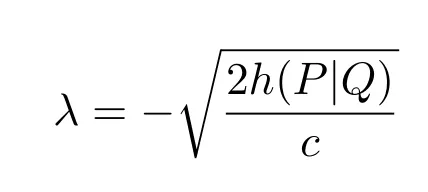
处取得最大值

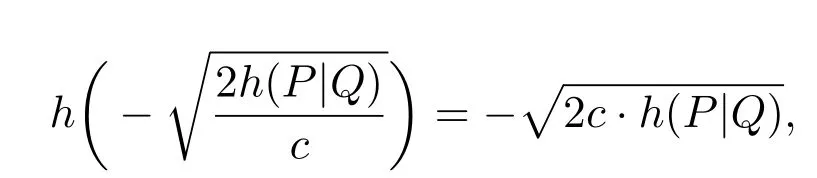
故在(32)式中令

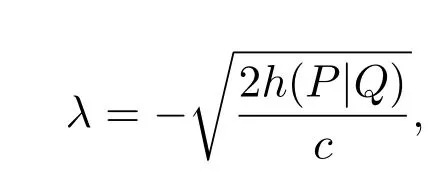
有

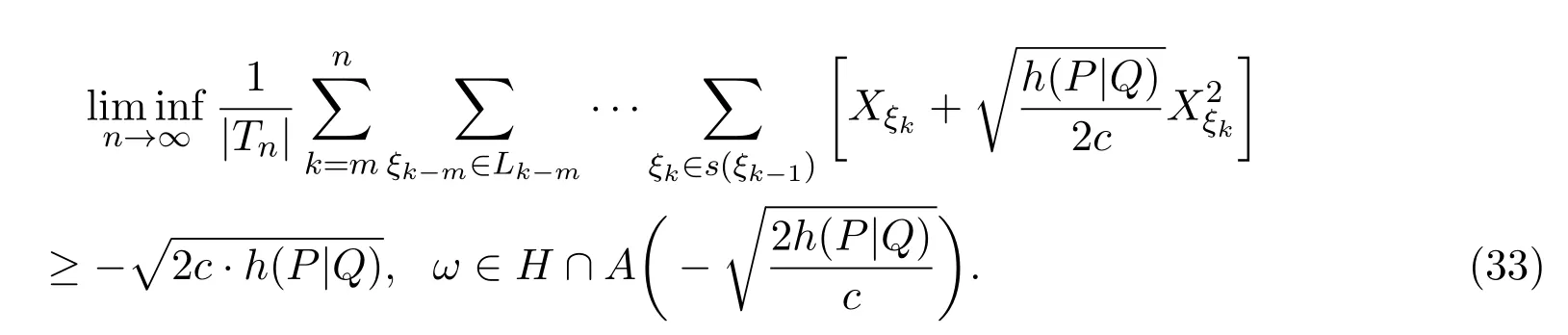
又由于

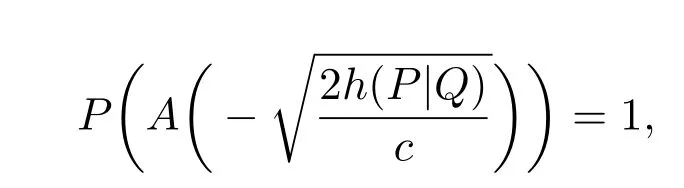
则由(33)式知(18)式成立.

若c=0，将λ=−1代入(32)式,有

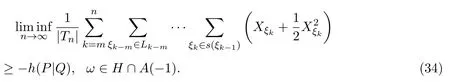
因P(A(−1))=1,则由 (34)式知 (20)式成立.

推论 3.1在定理3.1的条件下,若

则有

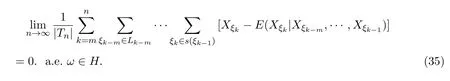
证明在(17)式和(18)式中令h(P|Q)=0 a.e.,有

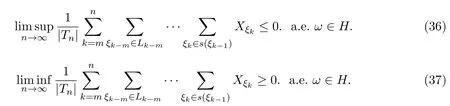
由(36)式和(37)式以及定理3.1条件可得(35)式成立.

[1]Spitzer F.Markov random fi elds on an in fi nite trees[J].Ann.Probab.,1975,3:387-398.

[2]Liu W,Yang W G.The Markov approximation of the sequences of N-valued random variables and a class of small deviation theorems[J].Stochastic Process Appl.,2000,89:117-130.

[3]Peng W C,Yang W G.A class of small deviation theorems for functionals of random fi elds on a homogeneous tree[J].J.Math.Anal.Appl.,2010,361:293-301.

[4]Yang W G.A class of small deviation theorem for the sequences ofN-valued random variables with respect to mth-order nonhomogeneous Markov chains[J].Acta Mathematica Scientia,2009,29A(2):517-527.

[5]Shi Zhiyan.Some strong deviation theorems for stochastic process indexed by a tree[J].Pakistan Journal of Statistics,2013,29(3):323-337.

[6]Doob J L.Stochastic Processes[M].New York:Wiley,1953.

Many limit properties of transition matrix for a nonhomogeneous Markov chain indexed by a tree

Jin Shaohua,Yu Kaili,Ren Shuangshuang,Li Xiaoxue
(College of Science,Hebei University of Technology,Tianjin 300401,China)

In recent years,the tree model has attracted a great deal of interest among scientists from various research fi elds such as physics,probability theory,information theory etc.Moreover,stochastic process indexed by a tree has become a hot topic in the fi eld of the probability theory in recent years.The researh of the strong limit theorem has held an important position in the development process of probability theory,and the strong limit theorem is one of the central issues of the international probability theory.In this paper,through introducing the concept of sample divergence rate,constructing non-negative martingale and applies Doob′s martingale convergence theorem to the research of a.e.convergence,many limit properties of transition matrix form-ordered countable non-homogeneous Markov chains on a non-homogeneous tree are obtained.

non-homogeneous tree,martingale,Markov chain,strong limit theorem

2010 MSC:60B12

O177.91

A

1008-5513(2017)06-0551-09

10.3969/j.issn.1008-5513.2017.06.001

2017-09-25.

河北工业大学研究生矩阵论示范课程建设项目(121031).

金少华(1965-),博士,教授，研究方向:概率论极限定理.